
3Линейка / Задачник-3 / Глава 9(2)
.doc
п)
 .
.
9.1.2.
Найдите квадрат жордановой клетки
![]() .
.
9.1.3.
Найдите жорданову форму квадрата
жордановой клетки
![]() при
при
![]() .
.
9.1.4.
Найдите жорданову форму квадрата
жордановой клетки
![]() ,
если
,
если
а) k=4;
б) k=5.
9.1.5. Постройте корневое подпространство для следующих матриц:
а)
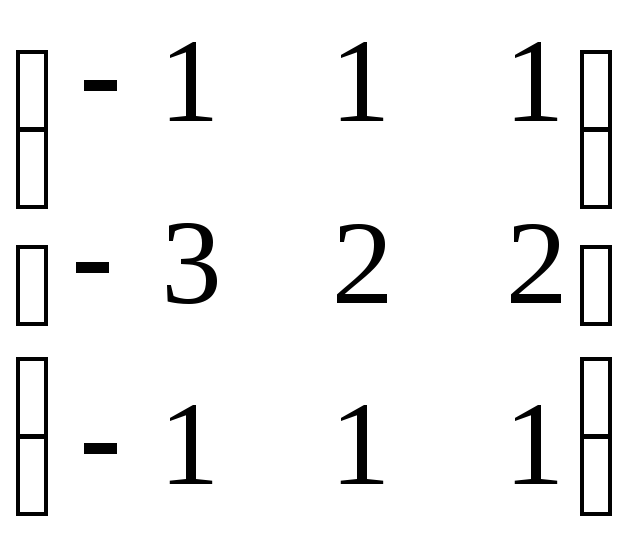 ;
б)
;
б)
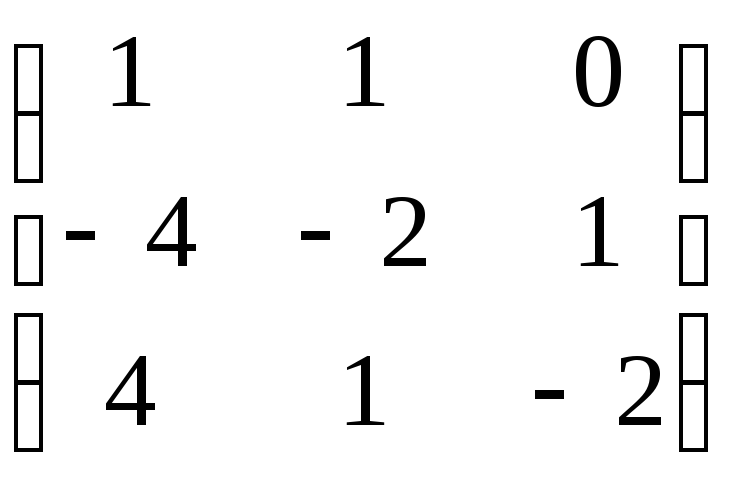 .
.
9.1.6.
Найдите канонический базис и жорданову
форму оператора дифференцирования в
пространстве
![]() .
.
9.1.7.
В пространстве многочленов
![]() найдите жорданову форму оператора
найдите жорданову форму оператора
![]() .
.
§ 9.2. λ – МАТРИЦЫ
Квадратная матрица, элементами которой являются многочлены от λ, называется λ – матрицей (полиномиальной матрицей). Степенью λ – матрицы называется максимальная из степеней многочленов, образующих элементы матрицы.
Элементарными преобразованиями λ – матриц называются преобразования следующих типов:
1) перестановка между собой двух каких – либо строк или столбцов матрицы;
2) прибавление к строке какой – либо другой строки, умноженной на некоторый многочлен φ(λ), и, аналогично, прибавление к столбцу другого столбца, умноженного на некоторый многочлен;
3) умножение строки или столбца на некоторое число, отличное от нуля.
Две λ – матрицы А(λ) и В(λ) называются эквивалентными, если одна может быть получена из другой при помощи конечного числа элементарных преобразований. Эквивалентность λ – матриц записывается следующим образом: А(λ)~В(λ).
Всякая λ – матрица может быть элементарными преобразованиями приведена к виду
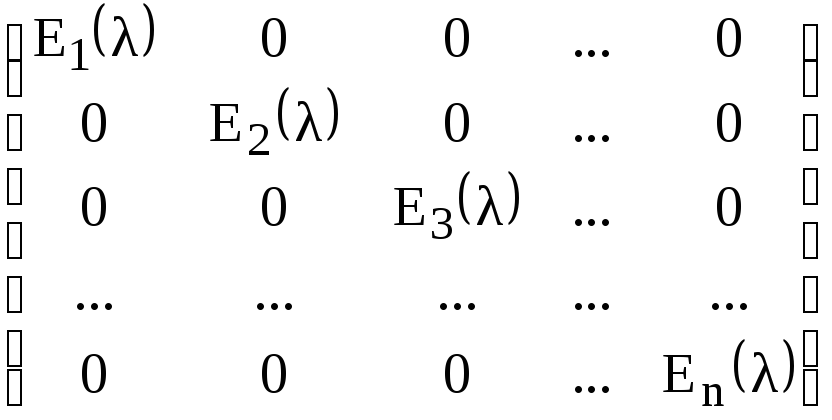 ,
(9.2.1)
,
(9.2.1)
где
многочлены
![]() ,
стоящие по диагонали, имеют старшие
коэффициенты, равные единице, многочлен
,
стоящие по диагонали, имеют старшие
коэффициенты, равные единице, многочлен
![]() делится на
делится на
![]() ,
,
![]() делится на
делится на
![]() и т. д. Этот вид называется нормальной
диагональной формой λ
– матрицы,
а многочлены
и т. д. Этот вид называется нормальной
диагональной формой λ
– матрицы,
а многочлены
![]() – инвариантными
множителями.
– инвариантными
множителями.
Нормальная
диагональная форма λ
– матрицы
А(λ)
определяется по ней однозначно. Если
![]() – наибольший общий делитель миноров
k–порядка
матрицы А(λ),
а
– наибольший общий делитель миноров
k–порядка
матрицы А(λ),
а
![]() ,
то элементы нормальной диагональной
формы (9.2.1) определяются по формулам
,
то элементы нормальной диагональной
формы (9.2.1) определяются по формулам
![]() ,
,
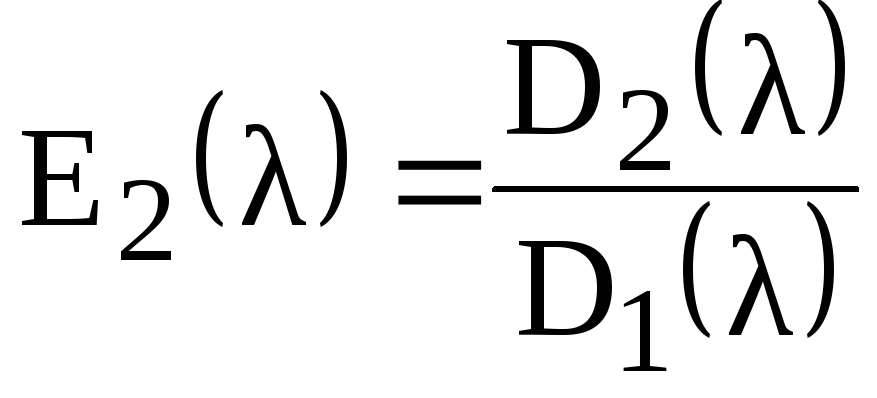 ,
,
. . . . . . . . . . (9.2.2)
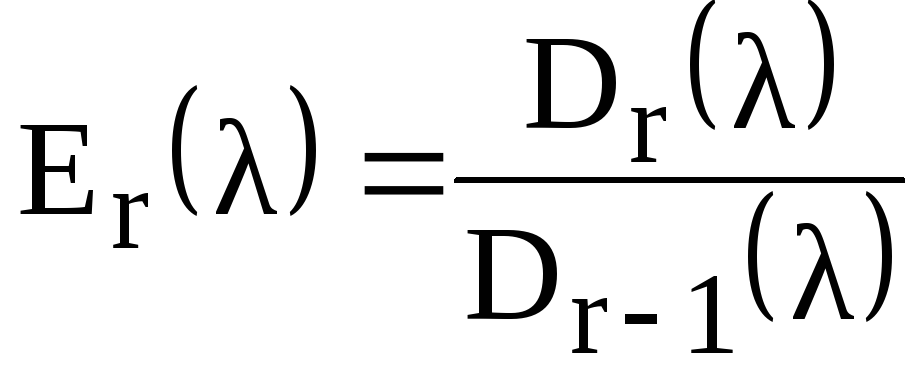 ,
,
![]() .
.
Таким образом, система инвариантных множителей λ – матрицы может быть получена с помощью либо элементарных преобразований, либо наибольших общих делителей ее миноров.
Для того чтобы две λ – матрицы А(λ) и В(λ) были эквивалентны, необходимо и достаточно, чтобы они имели одни и те же инвариантные множители.
Числовые
матрицы А и В одного порядка подобны
![]() тогда и только тогда, когда инвариантные
множители λ
– матриц
тогда и только тогда, когда инвариантные
множители λ
– матриц
![]() и
и
![]() совпадают между собой (критерий
подобия матриц).
совпадают между собой (критерий
подобия матриц).
Пусть
матрица А имеет жорданову нормальную
форму J,
в которой имеется p
клеток порядков
![]()
![]() ,
отвечающих собственному значению
,
отвечающих собственному значению
![]() ,
q
клеток порядков
,
q
клеток порядков
![]()
![]() ,
отвечающих собственному значению
,
отвечающих собственному значению
![]() ,
и т. д.; тогда инвариантные множители
,
и т. д.; тогда инвариантные множители
![]() матрицы
матрицы
![]() имеют вид
имеют вид
![]() ,
,
![]() ,
,
![]() ,
,
. . . . . . . . . . . . . . . . . . . .
Таким
образом, задание последовательности
инвариантных множителей
![]() полностью определяет жорданову нормальную
форму матрицы А; собственные значения
полностью определяет жорданову нормальную
форму матрицы А; собственные значения
![]() получаются как корни уравнения
получаются как корни уравнения
![]() .
Размеры же
.
Размеры же
![]() клеток, отвечающих данному собственному
значению
клеток, отвечающих данному собственному
значению
![]() ,
равны степеням, с которыми
,
равны степеням, с которыми
![]() содержится соответственно в
содержится соответственно в
![]()
Матрица
А имеет простую структуру тогда и только
тогда, когда все инвариантные множители
λ
– матрицы
![]() имеют только простые корни.
имеют только простые корни.
Скалярный
многочлен φ(λ)
называется
аннулирующим
многочленом
квадратной матрицы А, если φ![]() .
В частности, одним из аннулирующих
многочленов матрицы является ее
характеристический многочлен. Многочлен
наименьшей степени среди ненулевых
аннулирующих многочленов матрицы А со
старшим коэффициентом 1 называется
минимальным
многочленом
матрицы А. Любой аннулирующий многочлен
матрицы делится на ее минимальный
многочлен.
.
В частности, одним из аннулирующих
многочленов матрицы является ее
характеристический многочлен. Многочлен
наименьшей степени среди ненулевых
аннулирующих многочленов матрицы А со
старшим коэффициентом 1 называется
минимальным
многочленом
матрицы А. Любой аннулирующий многочлен
матрицы делится на ее минимальный
многочлен.
Минимальный
многочлен ψ(λ)
матрицы
А равен последнему инвариантному
множителю
![]() λ – матрицы
λ – матрицы
![]() .
.
Пример 1. При помощи инвариантных множителей найдите жорданову нормальную форму матрицы
 .
Укажите минимальный многочлен этой
матрицы.
.
Укажите минимальный многочлен этой
матрицы.
Решение.
Запишем λ
– матрицу
![]() и,
воспользовавшись методикой, подробно
изложенной в книге [6, §22], приведем ее к
нормальной диагональной форме:
и,
воспользовавшись методикой, подробно
изложенной в книге [6, §22], приведем ее к
нормальной диагональной форме:
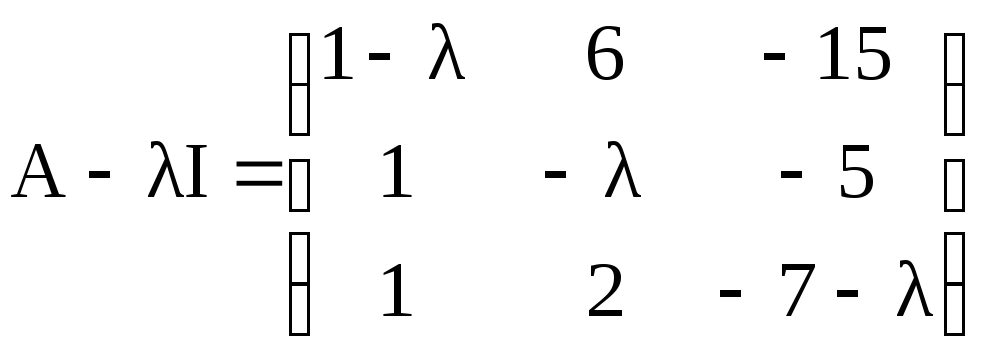 .
Поменяем местами первую и вторую строки:
.
Поменяем местами первую и вторую строки:
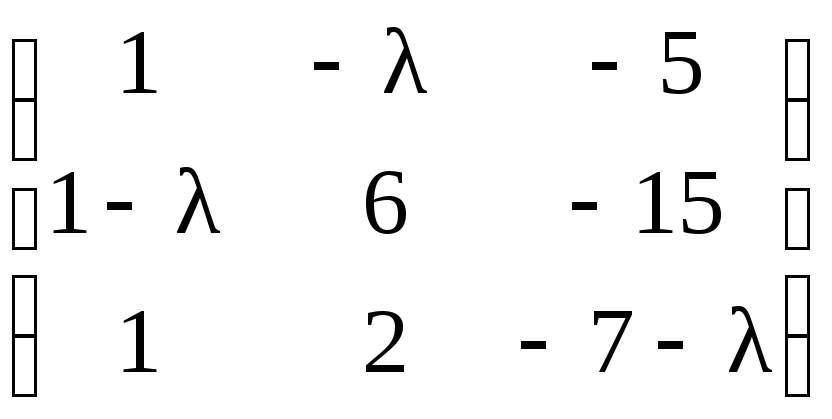 .
Теперь, прибавляя ко второму и третьему
столбцам первый, предварительно
умноженный соответственно на λ,
5, получим
.
Теперь, прибавляя ко второму и третьему
столбцам первый, предварительно
умноженный соответственно на λ,
5, получим
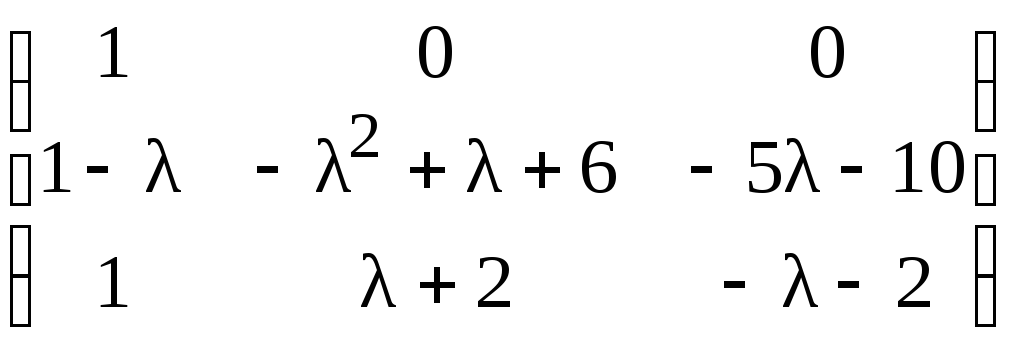 .
Прибавляя ко второй и третьей строкам
первую, предварительно умноженную
соответственно на
.
Прибавляя ко второй и третьей строкам
первую, предварительно умноженную
соответственно на
![]() ,
–1, получим
,
–1, получим
 .
Поменяем местами вторую и третью строки:
.
Поменяем местами вторую и третью строки:
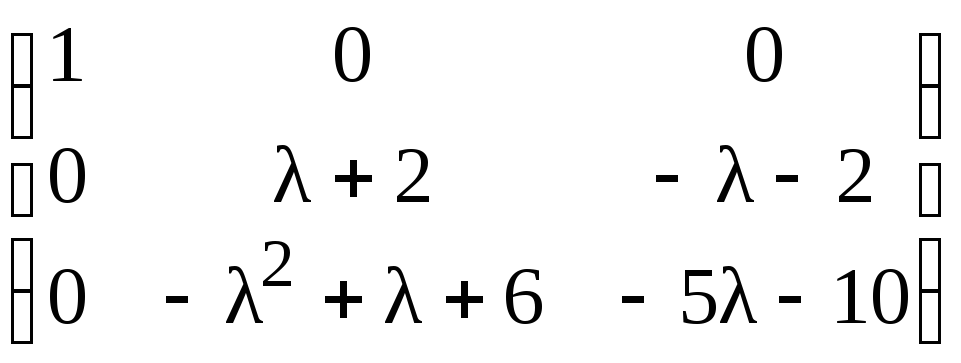 .
Прибавляя к третьему столбцу второй,
найдем:
.
Прибавляя к третьему столбцу второй,
найдем:
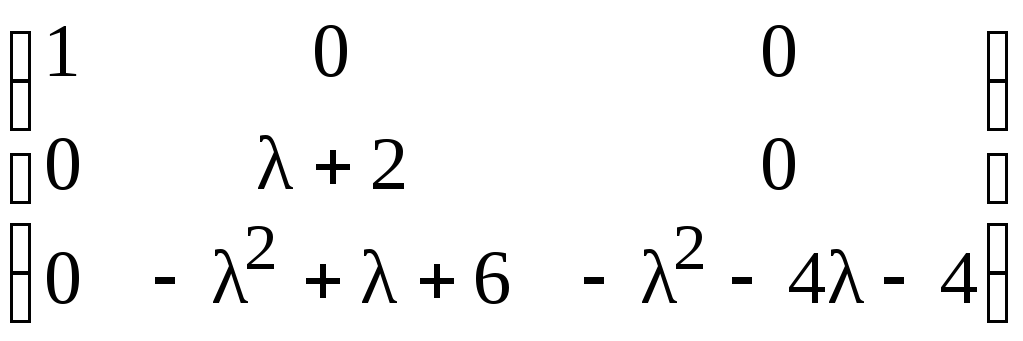 .
Прибавляя к третьей строке вторую,
умноженную на
.
Прибавляя к третьей строке вторую,
умноженную на
![]() ,
получим:
,
получим:
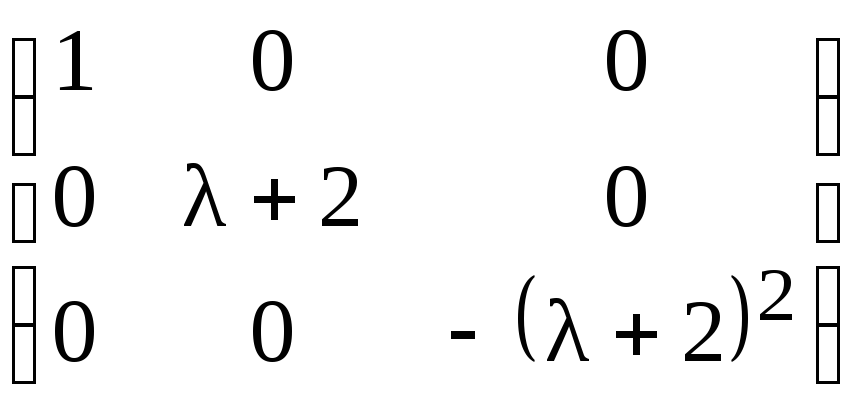 .
Умножая третий столбец на (–1), приходим
к нормальной диагональной форме λ–матрицы
.
Умножая третий столбец на (–1), приходим
к нормальной диагональной форме λ–матрицы
![]() :
:
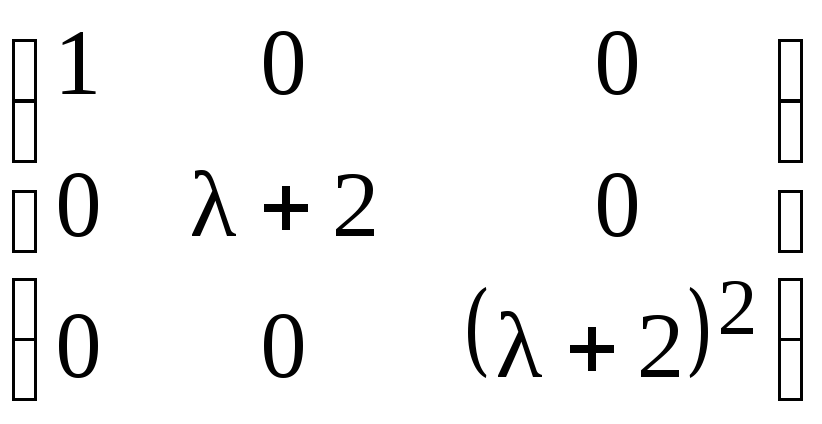 ,
инвариантные множители которой
,
инвариантные множители которой
![]() ,
,
![]() ,
,
![]() позволяют составить жорданову нормальную
форму
позволяют составить жорданову нормальную
форму
 и минимальный многочлен
и минимальный многочлен
![]() .
.
Пример
2.
Выясните, подобны ли между собой матрица
А из примера 1 и матрица
 .
.
Решение.
Найдем инвариантные множители λ
– матрицы
![]() ,
для чего приведем ее к нормальной
диагональной форме.
,
для чего приведем ее к нормальной
диагональной форме.
 .
Умножим второй столбец на
.
Умножим второй столбец на
![]() и поменяем местами его с первым столбцом:
и поменяем местами его с первым столбцом:
 .
Прибавляя ко второму и третьему столбцам
первый, предварительно умноженный на
.
Прибавляя ко второму и третьему столбцам
первый, предварительно умноженный на
![]() ,
15, получим:
,
15, получим:
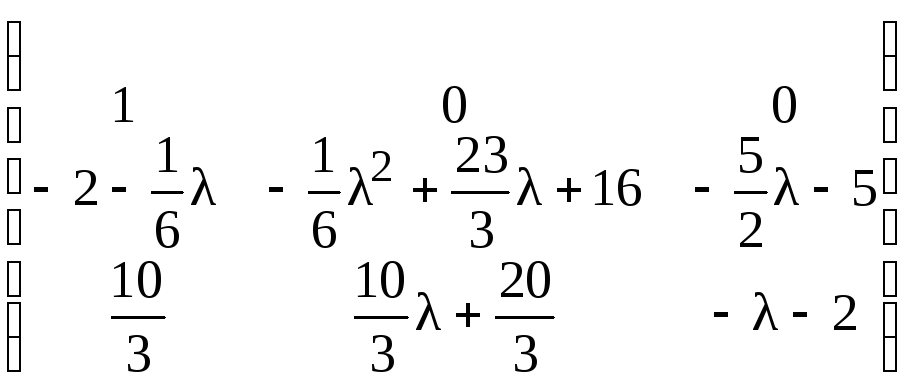 .
Теперь, прибавляя ко второй и третьей
строкам первую, предварительно умноженную
на
.
Теперь, прибавляя ко второй и третьей
строкам первую, предварительно умноженную
на
![]() ,
,
![]() ,
найдем:
,
найдем:
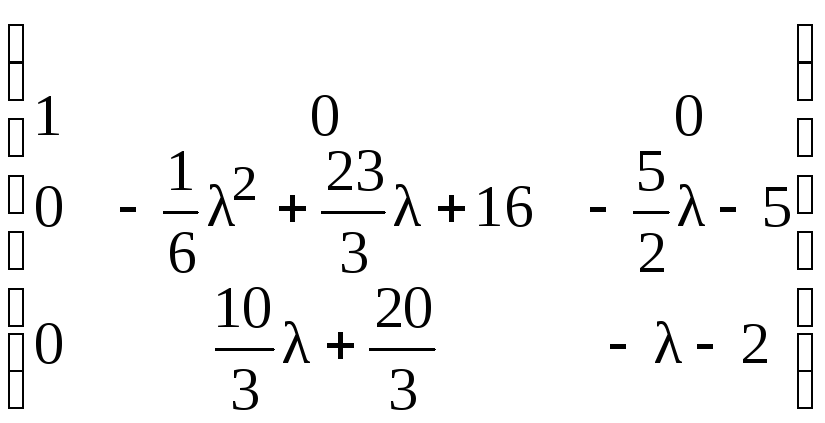 .
Третий столбец умножим на (–1) и поменяем
местами со вторым столбцом. Имеем:
.
Третий столбец умножим на (–1) и поменяем
местами со вторым столбцом. Имеем: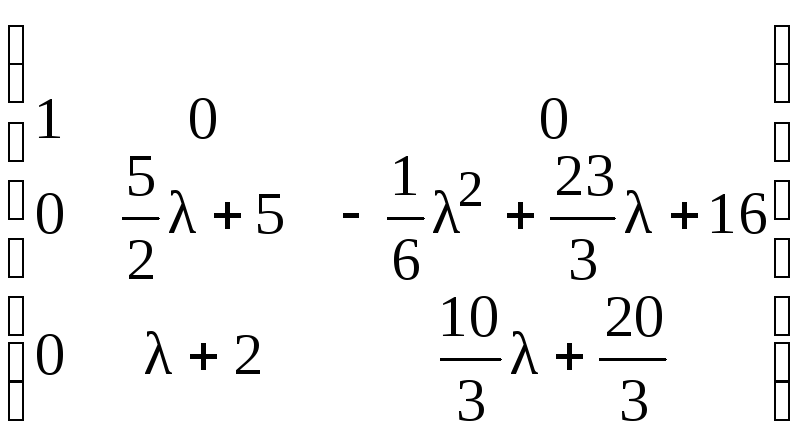 .
Поменяем местами вторую и третью строки:
.
Поменяем местами вторую и третью строки:
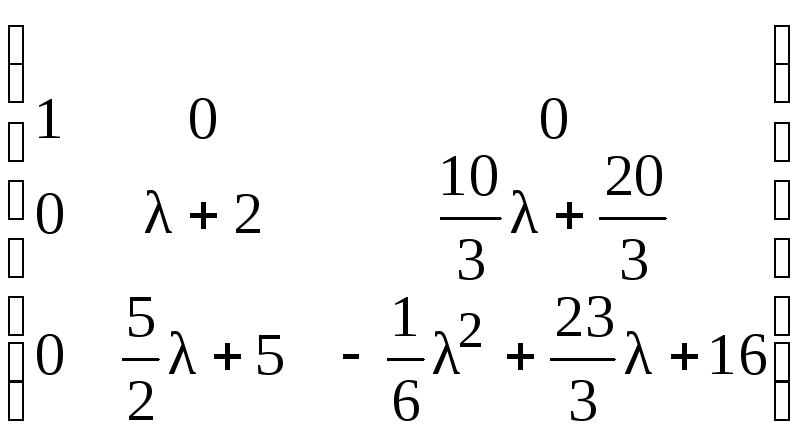 .
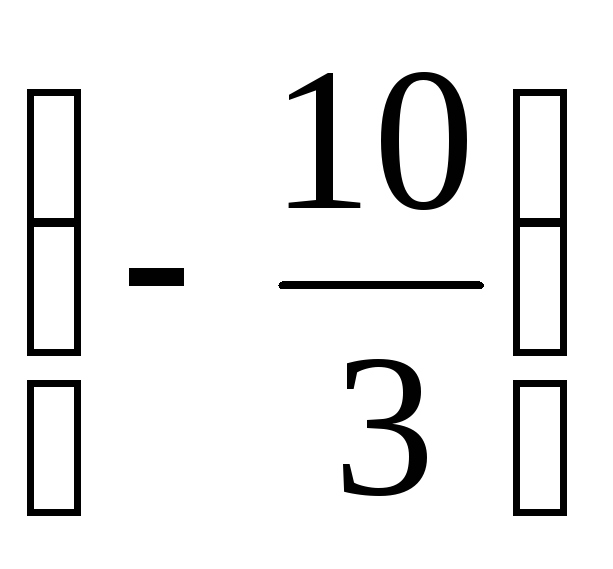
Прибавляя к третьему столбцу второй,
предварительно умноженный на
.
Прибавляя к третьему столбцу второй,
предварительно умноженный на
 ,
получим:
,
получим:
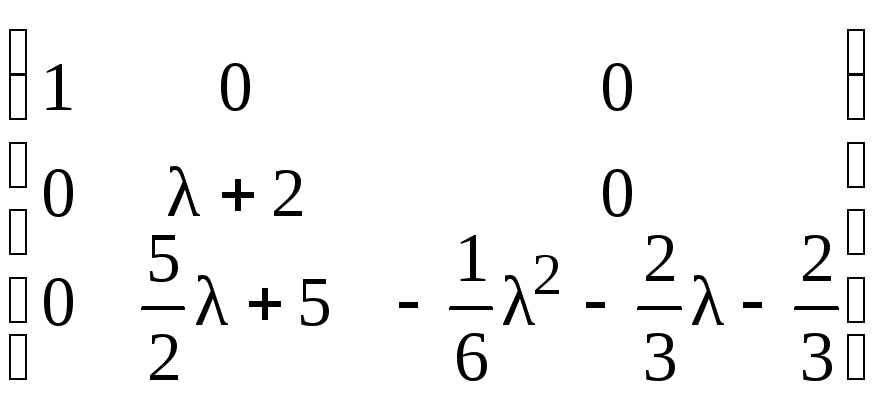 .
Прибавляя к третьей строке вторую,
предварительно умноженную на
.
Прибавляя к третьей строке вторую,
предварительно умноженную на
![]() ,
найдем:
,
найдем:
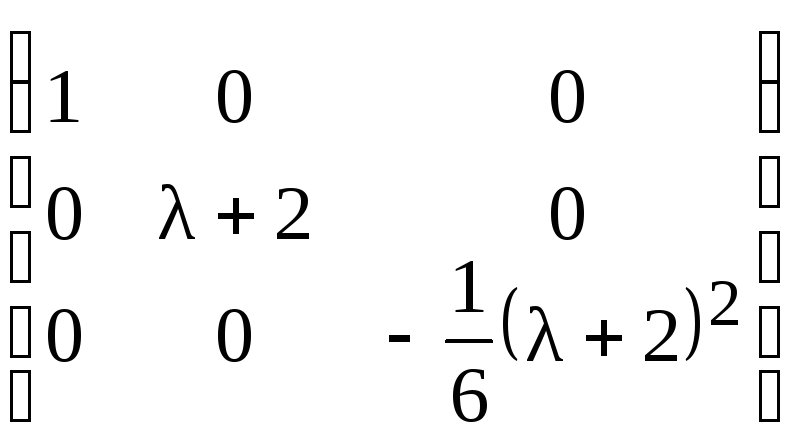 .
Умножая третий столбец на (–ф6), приходим
к нормальной диагональной форме λ
– матрицы
.
Умножая третий столбец на (–ф6), приходим
к нормальной диагональной форме λ
– матрицы
![]() :
:
 .
Выпишем инвариантные множители этой
матрицы:
.
Выпишем инвариантные множители этой
матрицы:
![]() ,
,
![]() ,
,
![]() .
Поскольку инвариантные множители λ
– матриц
.
Поскольку инвариантные множители λ
– матриц
![]() и
и
![]() между собой совпадают, согласно критерию
подобия матриц матрицы А и В подобны.
между собой совпадают, согласно критерию
подобия матриц матрицы А и В подобны.
9.2.1. Путем элементарных преобразований приведите следующие λ – матрицы к нормальной диагональной форме:
а)
 ;
б)
;
б)
 ;
в)
;
в)
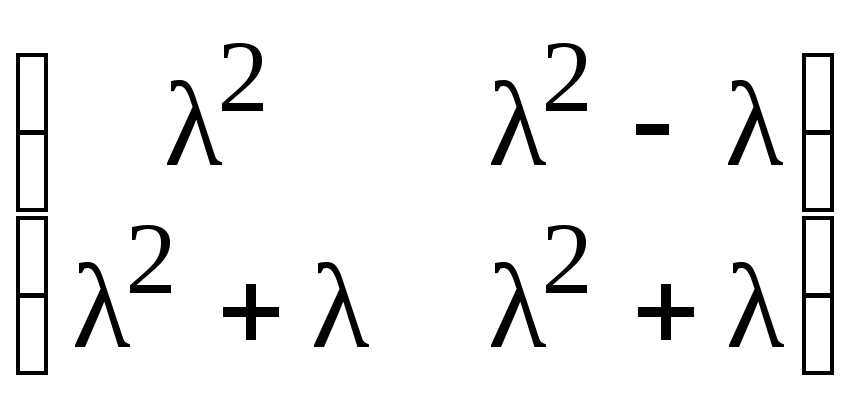 ;
;
г)
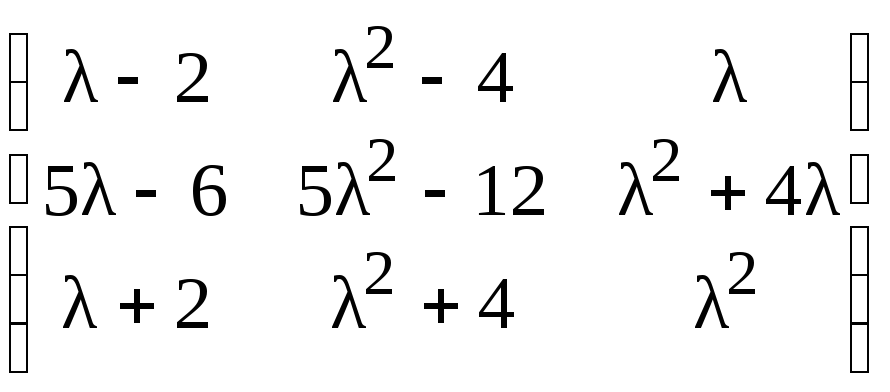 ;
д)
;
д)
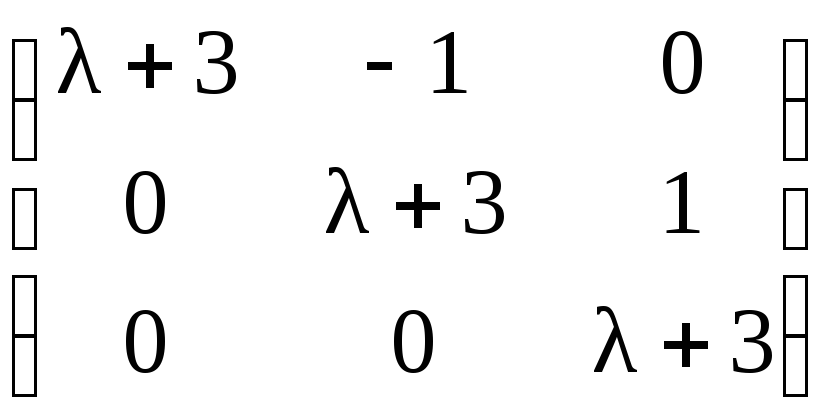 ;
;
е)
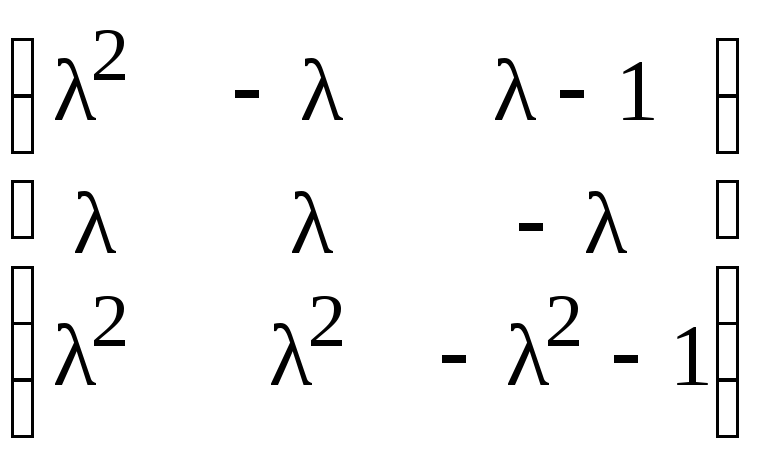 .
.
9.2.2. При помощи наибольших общих делителей миноров приведите следующие λ – матрицы к нормальной диагональной форме:
а)
 ;
б)
;
б)
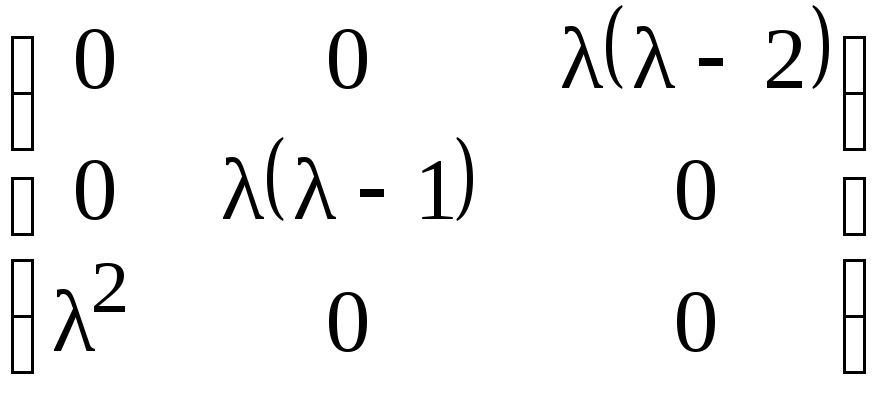 ;
;
в)
 ;
г)
;
г)
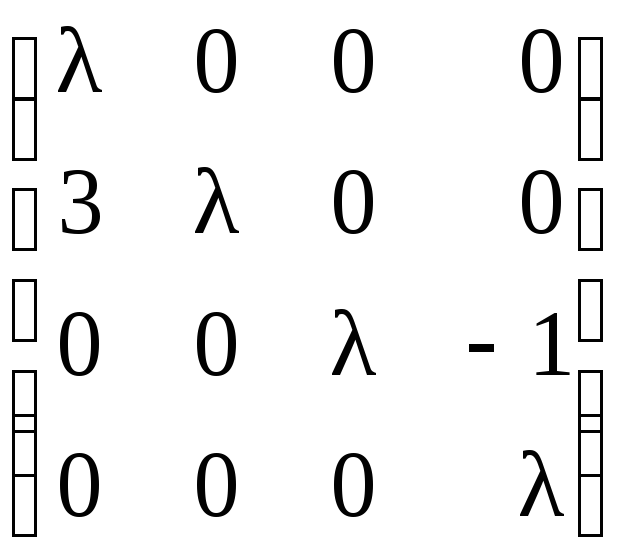 ;
д)
;
д)
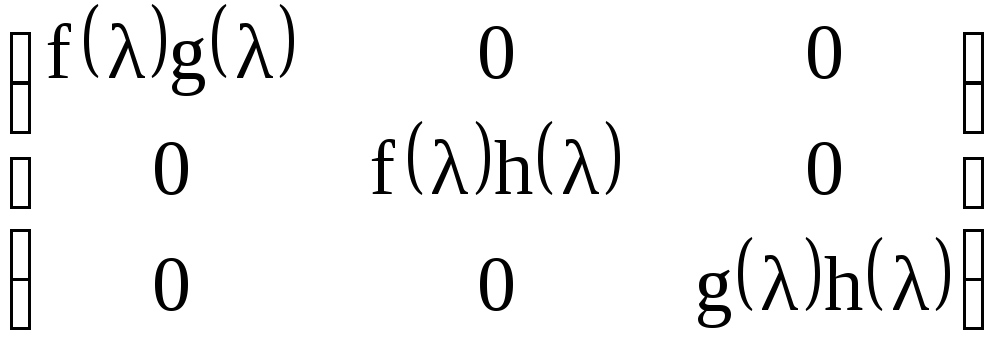 ,
,
где
![]() – попарно взаимно простые многочлены
от λ
со старшими коэффициентами, равными 1.
– попарно взаимно простые многочлены
от λ
со старшими коэффициентами, равными 1.
9.2.3.
Найдите жорданову нормальную форму J
матрицы А, если даны инвариантные
множители
![]()
![]() λ
– матрицы
λ
– матрицы
![]() :
:
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ,
,
![]() .
.
9.2.4. При помощи инвариантных множителей постройте жорданову нормальную форму следующих матриц:
а)
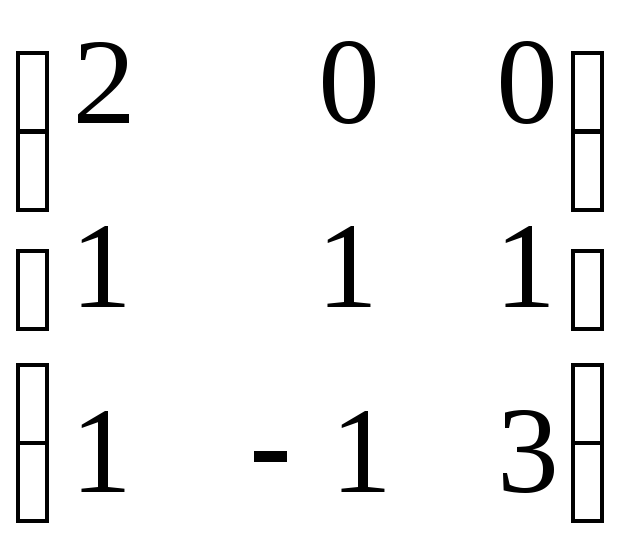 ;
б)
;
б)
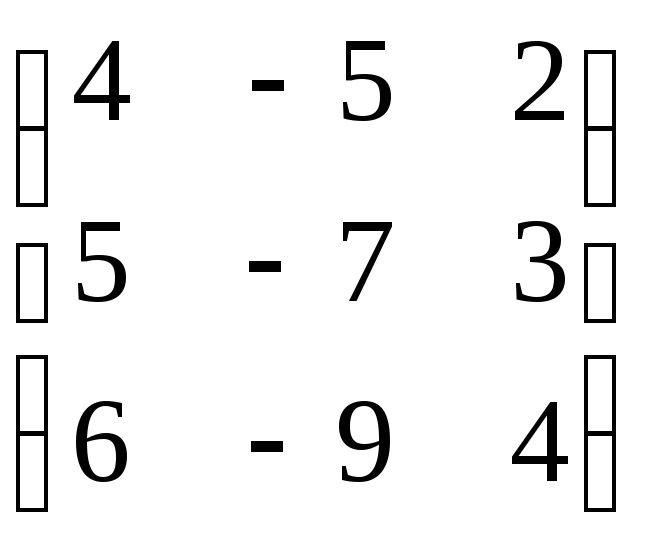 ;
в)
;
в)
 ;
;
г)
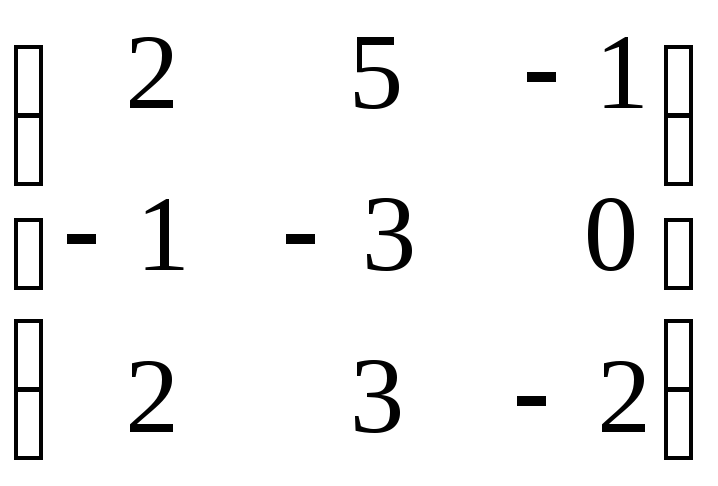 ;
д)
;
д)
 ;
е)
;
е)
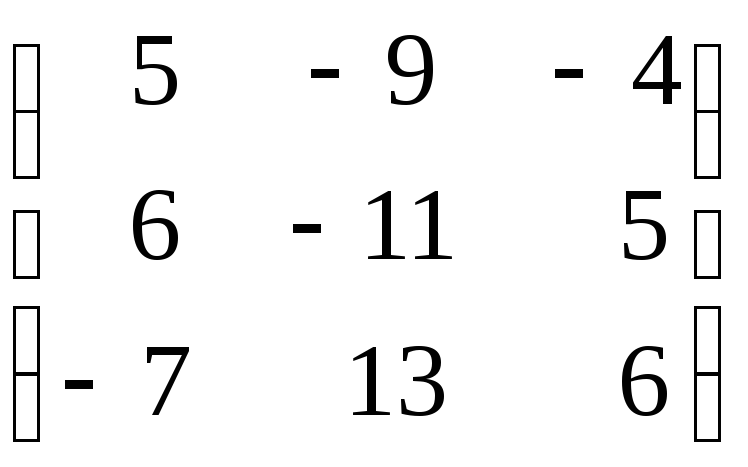 .
.
9.2.5. Выясните, являются ли подобными матрицы:
а)
 и
и
 ;
;
б)
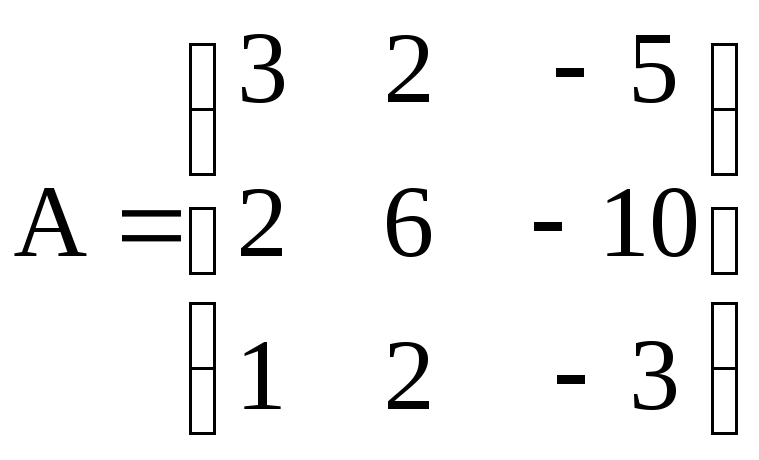 и
и
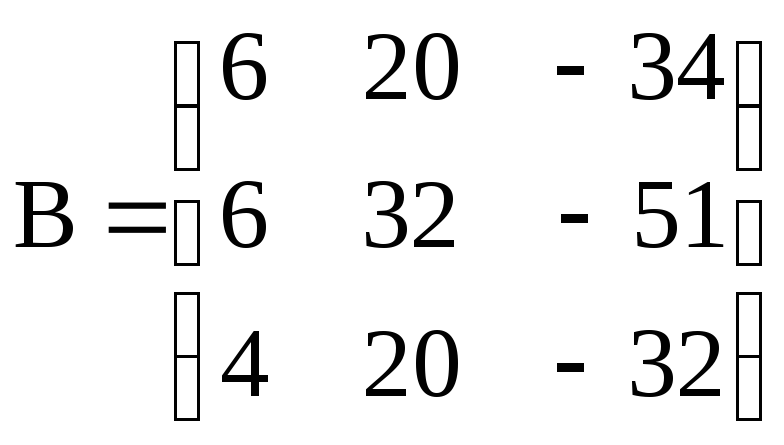 ;
;
в)
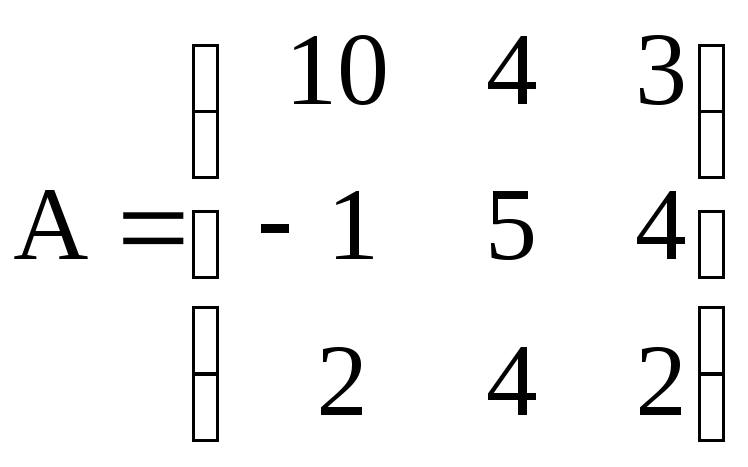 и
и
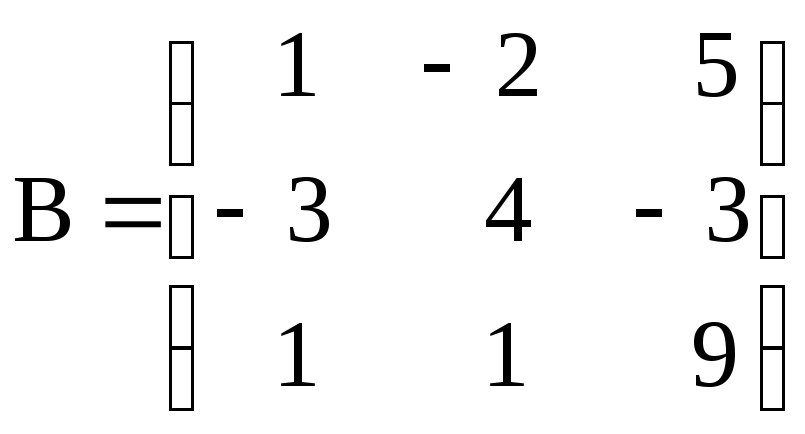 ;
;
г)
 и
и
 .
.
9.2.6. Приведите пример двух не подобных матриц, характеристические и минимальные многочлены которых одни и те же.
9.2.7. Найдите минимальные многочлены следующих матриц:
a)
 ;
б)
;
б)
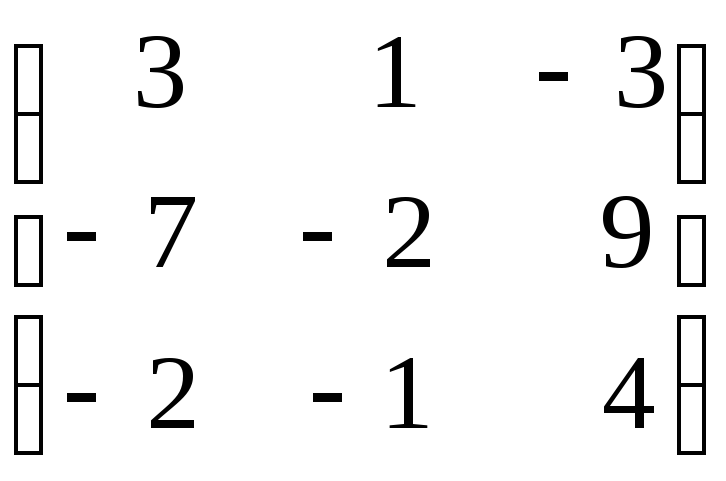 ;
в)
;
в)
 .
.
