2Дискретка / Задачники / 1.Теория множеств(задачи)

47. Постройте бинарное отношение, обладающее следующими свойствами, или докажите, что такого не существует:

				Свойства
	№	рефлек-	иррефлек-	симметрич-	антисим-	транзитив-
		сивность	сивность	ность	метричность	ность
	1	+	–	–	–	–
	2	–	+	–	–	–
	3	–	–	–	–	–
	4	+	–	–	–	+
	5	–	+	–	–	+
	6	–	–	–	–	+
	7	+	–	+	–	–
	8	–	+	+	–	–
	9	–	–	+	–	–
	10	+	–	+	–	+
	11	–	+	+	–	+
	12	–	–	+	–	+
	13	+	–	–	+	–
	14	–	+	–	+	–
	15	–	–	–	+	–
	16	+	–	–	+	+
	17	–	+	–	+	+
	18	–	–	–	+	+
	19	+	–	+	+	–
	20	–	+	+	+	–
	21	–	–	+	+	–
	22	+	–	+	+	+
	23	–	+	+	+	+
	24	–	–	+	+	+

Например, в первом варианте требуется построить рефлексив- ное, но не иррефлексивное, не симметричное, не антисимметричное, не транзитивное бинарное отношение.

14

48. Построить все классы эквивалентности по отношению P Ì A2 , если:

1) A = {1,2,3} ,

а) P =	{	(	)			(	2,2			)		,		(	3,3			)}				,
	{	1,1 ,				(				)								)						)					(						)					(						)				(				)				(				)				(	)}
б) P =		(	)				2,2						(							,		(										3,3					,						2,3					,				3,2												,				;
		1,1 ,										, 1,2											2,1 ,																																	, 1,3											3,1
{													}
2) A = 1,2,3,4,5,6,7,8																)				(				)				(						)					(						)					(				)				(					)				ï
ï	(		)	(		2,2		)		,		(		3,3				,				4,4				,					5,5						,					6,6						,				7,7				,				8,8					,
ì	1,1 ,																																																																		ü
а) P = í																																																																			ý,
ï(1,3)	,(3,6),(4,7),(5,8),(1,6),(6,1),(8,5),(7,4),(6,3),(3,1)ï
î	(		)		(				)				(				)				(				)					(						)					(						)				(				)				(					)			þ
ï							2,2				,				3,3				,				4,4				,						5,5					,						6,6					,				7,7				,				8,8					,		ï
ì		1,1 ,																																																																		ü	;
б) P = í			2,3),(2,5),(3,5)																																																																	ý
ï(1,7),(																					,(4,8),(8,4),(5,3),(5,2),(3,2),(7,1)ï
î																																																																				þ

3)A = {-2,-1,4,5,6} , P = {(x, y) xy > 0};

4)A = ¥;

а) P = {(x, y)					x + y > 0},
б) P = {(x, y)					x + y четное число},
в) P = {(x, y)					x - y		M5};

5)A = ¡ \{0} , P = {(x, y) xy > 0};

6)A – множество компьютерных программ, написанных в НГТУ, P = {(x, y) x и y написаны на одном языке программирования}.

49. Пусть P = {(x, y) x, y Î[-2,4] и x2 = y2}. Доказать, что отно-

шение P являются отношением эквивалентности и определить сле- дующие классы эквивалентности: [1], [2], [0], [3], [-1/ 2], [4].

50. Пусть A = {1,2,3,4,5,6,7} . Определить отношение эквивалент-

ности P , разбивающее множество A следующим образом:
1)	{{ }		{			}		{			}}	,			4)	{{		}	{			}}	,
	1,7 ,			3,4,6 ,					2,5							1,2,3,4 ,				5,6,7
2)	{{						}}				,				5)	{{ }	,	{ }			{		}}	,
	1,2,3,4,5,6,7											{ }	{ }}			1,4		3,5		,	{	6,2,7
3)	{{ }	{ }			,	{ }	{ }			,	{ }			,	6)	{{ }	,	{ }				}	{ }}		.
	1 ,	2				3 ,	4				5 ,	6 ,	7			1,7		3,5		,		2,4 ,	6

15

51. Среди указанных отношений и обратных к ним найти функ- циональные отношения.

1){(x, y)

2){(x, y)

3){(x, y)

4){(x, y)

5){(x, y)

6){(x, y)

7){(x, y)

8){(x, y)

9){(x, y)

10){(x, y)

11){(x, y)

12){(x, y)

13){(x, y)

14){(x, y)

	x, y ¡ y = 5};									15) {(
	x, y ¡ x = 7};									16) {(
	x, y ¡ y = x2};									17)	{(
	x, y ¡+		y = x2};							18)	{(
	x, y ¡+		y = x2 + 4};							19) {(
	x, y ¡+		y = x2 − 9};							20) {(
	x, y ¡ y = x3};									21)	{(
	x, y ¡ y = tg x} ;									22) {(
	x, y ¡ y = ln x};
										23) {(
		x, y ¡+	y = ln x};
										24) {(
		x, y ¡	y = x2 };
										25) {(
		x, y ¡	y = x +			x			};
										26) {(
		x, y ¡	y2 = x2};
										27) {(
		x, y ¡	y = x[x]};
										28) {(

x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y) x, y)

x, y ¡ y = x(x−5)(x+5)}; x, y ¡ y2 + x2 = 4};

x ¡, y ¡+ y2 + x2 = 4}; x ¡+ , y ¡ y2 + x2 = 4}; x, y ¡+ y2 + x2 = 4} ;

x, y ¡ y = 4 − x2 };

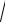x ¡, y ¡+ y = 4 − x2 }; x ¡+ , y ¡ y = 4 − x2 }; x, y ¡+ y = 4 − x2 };

x, y ¡ y2 + x2 ≤ 4};

x, y ¡ y = cos(arcsin x)};

x, y	[	]	}
		0;1	y =cos(arcsin x) ;
x, y ¡ y = sin(arcsin x)};
x, y	[	]	}
		0;1	y = sin(arcsin x) .

52. Для каждого функционального отношения из предыдущего задания

а) указать область определения и область значений; б) определить является ли функция инъекцией, сюръекцией,

биекцией; в) определить является ли функция всюду определенной или

частично определенной.

53. Найти образ и прообраз множества X относительно функции f (x) = x2 , если

1) X =

{

}

2) X =

(

4,9

]

;

3) X =

(

−4,9

]

.

4 ;

16

54.Найти образ множества (−4,4] относительно функции f (x) = x3 + 3x2 − 9x − 27 .

55.Найти прообраз множества (0;+¥] относительно функции f (x) = x3 + x2 - 6x .

56.Для функций f и g , заданных на множестве действительных чисел, найти f (g (x)) и g ( f (x)), если:

1)f (x) = x2 + 5, g (x) = x - 7 ;

2)f (x) = ln x , g (x) = x2 +1.

57.Пусть f – функция. При каких условиях отношение f −1 явля- ется функцией?

58.Пусть f : X → Y – функция. Доказать, что:

1)если A B X , то f ( A) f (B);

2)если A B Y , то f −1 ( A) f −1 (B).

59. *Доказать, что для любой функции f и произвольных A и B :

	1)	f ( A U B) = f ( A) U f (B),	4)	f −1 ( A U B) = f −1 ( A) U f −1 (B) ,
			5)	f −1 ( A I B) = f −1 ( A) I f −1 (B) ,
	2)	f ( A I B) Ì f ( A) I f (B),
			6)	f −1 ( A \ B) = f −1 ( A) \ f −1 (B),
	3)	f ( A) \ f (B) f ( A \ B) ,
				f −1 (		)Ì		.
			7)				f −1 (A)
					A

60. Привести пример функции f и множеств A и B таких, что

1)f (A I B) ¹ f ( A)I f (B),

2)f (A) \ f (B) ¹ f (A \ B).

61.*Привести примеры отношений P , для которых

1)P−1 (A I B) ¹ P−1 ( A)I P−1 (B),

2)P−1 (A \ B) ¹ P−1 ( A) \ P−1 (B),

3)P−1 (A) P−1 ( A).

17

62. Пусть f : X → Y – функция. Доказать, что f инъективна то- гда и только тогда, когда для всех подмножеств A и B множества

Xсправедливо тождество f ( A I B) = f ( A) I f (B).

63.Пусть X – конечное множество и f : X → X инъекция. Доказать,

что f биекция.

64.Пусть f : X → Y , g :Y → Z . Доказать, что

1) если f		и g – сюръекции, то f o g – сюръекция;
2) если	f	и g – инъекции, то	f o g – инъекция;
3) если	f	и g – биекции, то	f o g – биекция;
4) если	f	и g – биекции, то ( f o g )−1 = g−1 o f −1 .

65.Доказать, что:

1)всякое подмножество конечного множества конечно;

2)объединение конечного числа конечных множеств конечно;

3)прямое произведение конечного числа конечных множеств конечно.

66.Доказать, что:

1)	если A счетно, а B конечно, то A \ B счетно;
2)	если A счетно, а B конечно, то A U B счетно;
3)	если A и B счетны, то A U B счетно;
4)	если A и B счетны, то A× B счетно;

5)прямое произведение конечного числа счетных множеств

счетно.

6)если все Ai счетны, то UAi счетно.

i ¥

7) если все Ai конечны, не пусты и попарно не пересекаются, то

UAi счетно;

i ¥

67.Доказать, что:

1)множество целых чисел счетно;

2)множество рациональных чисел счетно;

3)множество алгебраических чисел счетно.

68.Доказать, что любое бесконечное подмножество счетного множества счетно.

18

69. Определить, являются ли бинарная операция коммутативной,
идемпотентной, если:
1) a\b				1	2			2) a\b		1	2	3			3) a\b			1	2	3
	1			1	1				1	1	1	3					1	1	2	3
2				2	2	2				1	1	1			2			2	2	1
						3				2	2	3			3			3	1	3
70. Определить, какими свойствами обладают операции:
1)			a\b		0	1					2)	a\b		0	1
			0		1	1						0		0	1
			1		0	1						1		1	1

71.					é1 2 3ù		, b =	é1 2	3ù
	Найти α oβ, если a = ê					ú		ê	ú .
					ë3 1 2û			ë1 3	2û
72.	Найти γ oα oβ и β oγ oα , если
		é1 2 3ù		é1 2 3ù		, g =	é1 2 3ù
a = ê			ú ,	b = ê	ú		ê	ú .
		ë2 3 2û		ë1 2 2û			ë2 3 1û
73.	Найти преобразование α , если
	é1 2 3ù		, boa =		é1 2 3ù		é1 2 3ù			é1 2 3ù
1) b = ê		ú			ê	ú ; 2)	b = ê		ú ,	a ob = ê	ú .
	ë1 3 2û				ë1 1 2	û	ë3 2 1û			ë	2 3 1û
74.	Найти α,		α oβoγ , γ oβ oα , если
b =		é1 2 3ù		é1 2 3ù		boa og =		é1 2 3ù
		ê	ú , g = ê		ú ,			ê	ú.
		ë2 1 3û		ë2 3 1û				ë1 1 2û
75.	Определить,			какими		свойствами			обладает		операция

a j b = 3ab2 , если:

1) j: ¡2 ® ¡, 2) j:{0,1,-1}2 ® {0,1,-1} , 3) j:{0,1}2 ® {0,1} .

76. Определить,	какими	свойствами обладает операция
a j b = a + b , если j: ¡2 ® ¡.
2
77. Определить,	является ли операция g : ¡2 ® ¡ дистрибутивной
относительно операции j: ¡2 ® ¡, если
1) a γ b = ab + a , a j b = a + b		, 2) a g b = aeb , a j b = a + b .
	2	2

19