Понятие функции

Определение 1. Пусть и _– непустые множества (произвольной природы!). Если каждому элементу (аргументу, переменной) по определенному правилуставится в соответствие единственный элемент(значение), то говорят, что на множествезаданафункция (илиоднозначное отображение). При этом: используется обозначение ,=– область определения функции (=– область значений, если для каждогонайдется такой аргумент, что).

Частные случаи:

по размерности значения:

1. вещественная (скалярная, числовая) функция – значения числовые ();

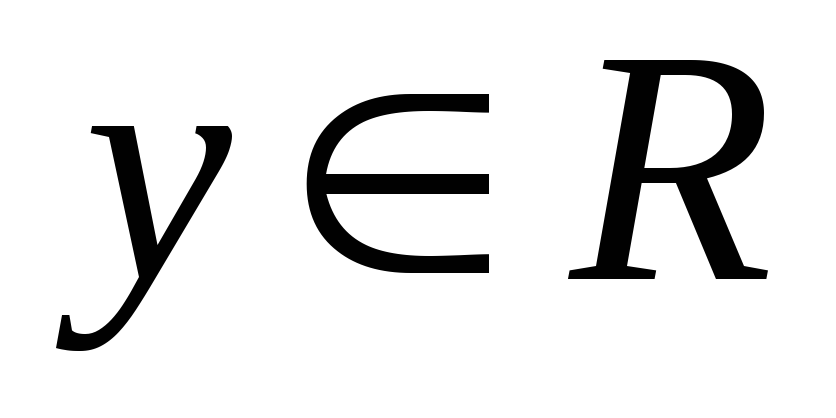2. векторная функция – значения векторные ();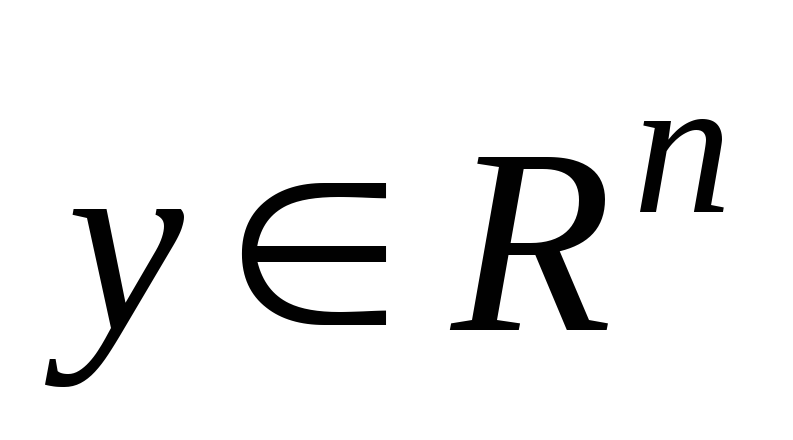

по размерности аргумента:

3. функция одной переменной – значения числовые ();

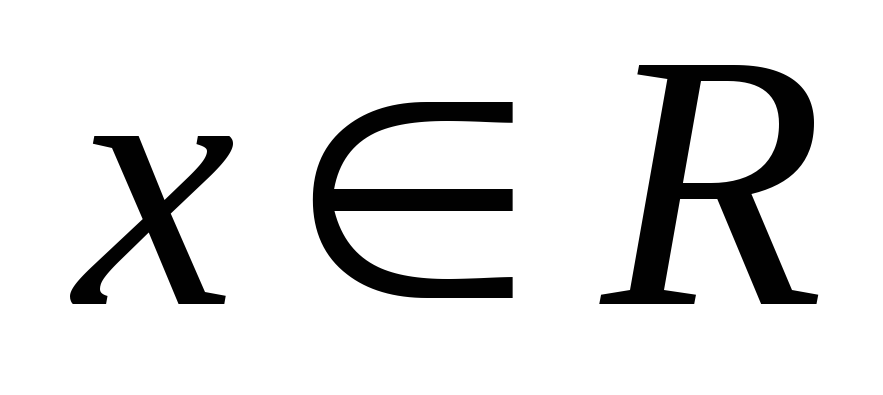4. функция многих переменных – значения 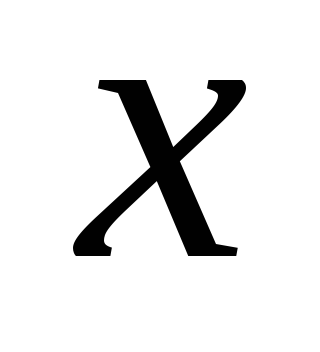векторные ().

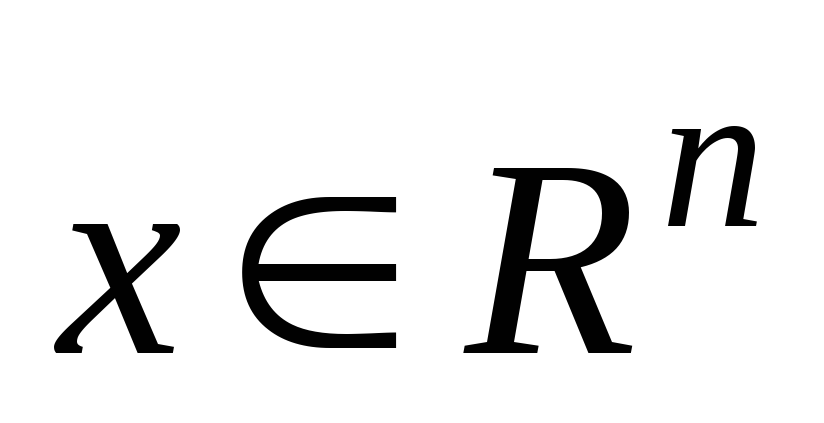Многочлен (полином) порядка – функция вида 1), 3):,.

Определение 2. Если функция задана на множестве, а функциязадана на множествеи имеет область значений, то функция, заданная на множестве, –сложная функция.

Определение 3. Множество точек (линия или поверхность),,, –график функции . Обозначается.

Частные случаи: 1) график вещественной функции одной вещественной переменной – линия на декартовой плоскости (такую линию каждая вертикальная прямая пересекает не более 1 раза);

2) график вещественной функции двух вещественных переменных – поверхность в трехмерном пространстве.

Примеры функций многих переменных в экономике:

1) Функция полезности от двух приобретенных товаров

а) ,где (),,;

б) ,где ,(),,;

в) функция Р. Стоуна , где() – минимально необходимое количество-го блага,() – относительные ценности благ для потребителя.

2) Производственная функция выражает результат производства от труда и капитала:

а) функция Кобба–Дугласа; б) функцияSEC .

Определение 4. Множество аргументов, при которых вещественная функция многих переменных принимает одинаковые значения, – поверхность уровня функции. Если, в частности, дана функция двух переменных , то множество точек, в которых,, – это линия уровня данной функции.

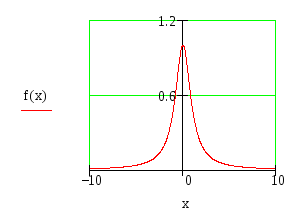
На рисунке – семейство гипербол – линий уровня ,для, построенных перебором значенийс некоторым шагом.

Семейство линий уровня дает представление о «рельефе» графика функции (подобно географической карте).

Пример. Найти линии уровня функции .

Решение. Линии уровня данной функции – это семейство кривых на плоскости , заданное уравнением. Преобразуем это уравнение: выделим полный квадрат по каждой переменной. Тогдаили. Полученное уравнение описывает семейство окружностей с центром в точкерадиуса().

Свойства функций

Определение 1. Функция называетсячётной (нечётной), если вместе со всяким и выполняется равенство().

График скалярной четной (нечетной) функции одной переменной расположен симметрично относительно оси (начала координат).

Определение 2. Функция называетсяпериодической, если существует Т>0, что вместе со всяким и.

Свойства Т-периодической функции достаточно определить на любом промежутке длиной Т из.

Определение 3. Скалярная функция одной переменной называетсявозрастающей (убывающей) на множестве , если для любыхиз неравенстваследует неравенство(). Если неравенство для значений функции строгое, то монотонность – строгая.