
Линейная алгебра
.doc

Решение:
1)
![]()
2) Каноническое уравнение прямой, проходящей через две данные точки
А1 (x1,y1,z1) и А2 (x2,y2,z2), имеет вид:
![]()
или в параметрическом
виде:
![]()
![]() ;
;
![]() .
.
Аналогично уравнение прямой, проходящей через две точки
А1 (x1,y1,z1) и А4 (x4,y4,z4), имеет вид:
![]() ;
;
![]() ;
;![]()
Замечание: ноль в знаменателе означает, что прямая, проходящая через точки
А1 (x1,y1,z1) и А4 (x4,y4,z4), перпендикулярна оси ОY.
Угол между двумя прямыми определяется по формуле:

3) Найдем уравнение плоскости ,проходящей через точки А1, А2 и А3.

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией на плоскость. Пусть прямая и плоскость заданы уравнениями
![]()
Тогда
![]()

4)
![]() ,
где h
– высота, опущенная из точки А3
на
,
где h
– высота, опущенная из точки А3
на
отрезок А1А2
с уравнением
![]()
Найдем уравнение перпендикуляра.
Запишем его
уравнение как
![]()
Условие
перпендикулярности прямых:
![]()
Условие прохождения через точку А3 (6;2;0)
![]()


Получили условие принадлежности искомого перпендикуляра плоскости
![]()
Тогда

Направляющий вектор искомой прямой находим как векторное произведение
![]() (-2;1;3)
и
(-2;1;3)
и
![]() (2;13;-3)
(2;13;-3)
![]() ;
;
![]() ;
;
![]()
Итак, уравнение перпендикуляра:
![]() или
или
![]()
и отрезок А1А2
с уравнением
![]()
их точку пересечения P (3;2;-2) находим путем решения системы линейных уравнений.
Длина перпендикуляра
![]()
![]()
5) Рассмотрим
векторы
![]() ,
,
![]() и
и
![]() ,
на которых построена пирамида.
,
на которых построена пирамида.
Зная координаты начала и конца каждого вектора, получаем объема пирамиды на основании формулы:

6) Из точки А4
(0;2;2) опускаем перпендикуляр, уравнение
плоскости
![]() :
:
![]()
Прямая, проходящая
через точку А4
(0;2;2) и перпендикулярная плоскости
![]() ,
имеет направляющий вектор
,
имеет направляющий вектор
![]() ,
,
следовательно, искомая прямая представляется уравнением
![]()
7) уравнение
плоскости, определяемой высотой
![]()
и точками А1 (3;2;-2) и А4 (0;2;2)
искомая плоскость определяется двумя прямыми: высотой пирамиды и гранью А1А4
уравнение грани А1А4:
![]() ;
;
![]()
Выразим прямые параметрически:
 и
и

Уравнение плоскости, проходящей через две пересекающиеся прямые:
![]() ,
,
![]()
![]()
Тогда уравнение плоскости


![]()
Решение:
Данные векторы образуют базис в Ln = L4 тогда и только тогда, когда число векторов равно n=4 и detA0, где A – матрица из координатных столбцов данных векторов.

Итак, заданные векторы действительно образуют базис в четырехмерном пространстве.
Найдем координаты
вектора
![]() в этом базисе.
в этом базисе.
Обозначим координаты
вектора
![]()
![]() или
или





x=1/3; y=2; z=3; t=1
координаты вектора
![]()
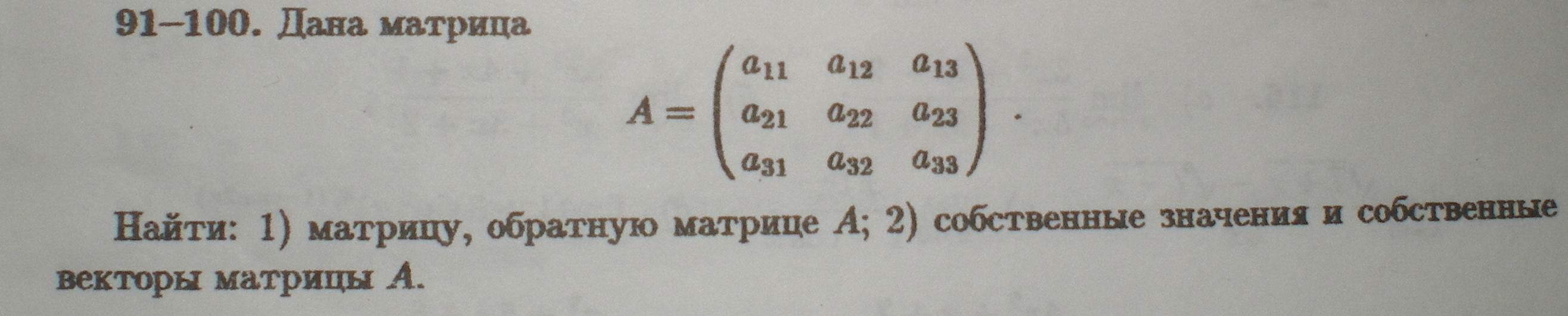

Решение:

Обозначим
![]()
Тогда



Число
и вектор-столбец
![]() называются собственными, если
называются собственными, если
![]()
Нам нужно, чтобы эта система имела нетривиальное (ненулевое) решение. А поскольку тривиальное решение у неё есть всегда, требуется, чтобы к-во решений было бесконечным. Это означает, что детерминант матрицы должен быть нулевым, что и даёт уравнение на собственные числа.
Для нахождения собственных значений матрицы A составляем характеристическое уравнение:


Имеет три корня: 1=-1; 2=1; 3=5.
Для корня 1=-1

![]() ,
где t – параметр
,
где t – параметр
Для корня 2=1
 ,
,
![]() ,
где t – параметр
,
где t – параметр
Для корня 2=5
 ,
,
![]() ,
где t – параметр
,
где t – параметр
