Учебное пособие по начертательной геометрии

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ДЕПАРТАМЕНТ КАДРОВОЙ ПОЛИТИКИ И ОБРАЗОВАНИЯ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ЧЕЛЯБИНСКИЙ ГОСУДАРСТВЕННЫЙ АГРОИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ»

Кафедра графики

	Утверждаю
Проректор по УР	А.А. Патрушев

Учебное пособие по начертательной геометрии

Челябинск 2 0 0 9

Учебное пособие предназначено для организации самостоятельной работы студентов заочного отделения, содержит классификацию геометрических образов, их пространственные и комплексные чертежи, а так же алгоритм решения позиционных и метрических задач.

Цель данного пособия - помочь студентам самостоятельно:

1.изучить теорию;

2.ответить на вопросы;

3.решить задачи соответствующего раздела.

Кроме того, пособие содержит образцы домашних графических работ и даны методические указания по их выполнению.

Данное учебное пособие поможет студентам при подготовке к экзаменам по начертательной геометрии.

Составители:

Назмутдинова Н.И. – старший преподаватель, ЧГАУ Торбеев И.Г. – канд. техн. наук, доцент, ЧГАУ

Лещенко Г.П. – канд. техн. наук, доцент кафедры графики, ЧГАУ Сазонов К.А. – канд. техн. наук, доцент, ЧГАУ.

Рецензенты:

Четыркин Ю.Б.- канд. техн. наук, доцент, ЧГАУ, Краснов В.А.- канд. техн. наук, доцент, ЮУрГУ

Ответственный за выпуск Торбеев И.Г. - зав. кафедрой графики (ЧГАУ)

Печатается по решению издательского совета ЧГАУ

© Челябинский государственный агроинженерный университет, 2009

2

Введение

Начертательная геометрия — раздел геометрии, в котором изучаются пространственные фигуры по их изображениям на плоскости, а также методы решения и исследования пространственных задач на плоском чертеже.

Вкурсе начертательной геометрии можно выделить три основных класса задач: позиционные, метрические и комбинированные. Задачи каждого класса имеют свои особенности и соответствующиеимприемы решения.

Позиционными называются задачи, в которых определяется относительное положение или общие элементы геометрических фигур.

Задачи, связанные с измерением расстояний и угловых величин, называются метрическими.

К классу комбинированных относятся задачи, рассматривающие совместно в различных сочетаниях позиционные и метрические свойства геометрических фигур.

Вкаждом классе, в свою очередь, можно выделить особую группу задач, в которых на искомое наложено два или более условий. Эти задачи называются комплексными.

Любую задачу, независимо от ее принадлежности к тому или иному классу, нужно сначала решить в пространстве - уяснить содержание и последовательность тех пространственных операций, при помощи которых определяются искомые элементы. В некоторых случаях для этого можно использовать модели или наглядные изображения. Алгоритм решения задачи в пространстве необходимо символически записать, пользуясь примерами, данными в пособии. Только после этого можно переходить к графической реализации алгоритма

-решению задачи на комплексном чертеже. Для этого необходимо уметь выполнять на комплексном чертеже построения, основанные на определенных теоретических положениях курса.

При решении задач надо иметь в виду, что начертательная геометрия оперирует не с самими геометрическими фигурами, а с их проекциями, и требование в условиях

3

«построить», «определить», «найти» и т.п. означает, что нужно построить проекции (не менее двух) искомых геометрических фигур.

Обозначение и символика:
Геометрическая фигура	- Ф
Точки пространства	- А, В, С…
	1, 2, 3, 4…
Слово <<точка>>	- (.)
Линии пространства	- а, в, с, d…
Линии уровня:
горизонталь	- h
фронталь	- f
Прямая проходящая через точки А и В	- (AB)
Отрезок прямой	- [AB]
Расстояние между точками А и В	- │AB│
Величина угла (АСВ)	- AĈB
Поверхности (плоскости)	- 0, P, λ, ∆…
Плоскости проекций	- П (пи)
Совпадают	- =
Конгруэнтны	-
Подобны	- ~
Параллельны	- ‖
Перпендикулярны	-
Скрещиваются	-
Пересекаются	- ∩
Объединяются (соединяются)	-
Касательные	-
Отображаются	- →
Логическое следствие	-
Принадлежит, является элементом	-
Включает, содержит	-
Вращение	-

4

Модели геометрических образов и их определитель:

Точка

Простейший геометрический образ пространства есть точка – одно из основных неопределяемых понятий геометрии. Точка как простейший элемент составляет суть всех последующих геометрических образов, состоящих из некоторого определенного множества точек пространства. На чертеже мы имеем не геометрическую точку, а ее образ, который обладает некоторыми малыми размерами. Это условное изображение мы считаем точкой и определяем как место пересечения двух линий.

Линия

Линия — траектория движущейся точки. Кривая линия обусловлена движением точки в постоянно изменяющемся направлении. Прямая линия определяется двумя точками, кривая — n точками.

Плоскость

Плоскость — часть пространства, определяемая элементами (точками, линиями). Плоскость бесконечна. Всякая плоская фигура есть часть какой-либо плоскости, поэтому ее называют отсеком плоскости. Плоскость считается построенной на комплексном чертеже, если заданы проекции; элементов ее определяющих.

Поверхность

В элементарной геометрии поверхность определяется как граница фигуры или совокупность всех последовательных положений движущейся линии (не вдоль себя).

Определитель

Определитель геометрического образа – необходимая и достаточная совокупность геометрических фигур и связей между ними, однозначно определяющих образ и реализующих закон его образования. Определитель описывается после буквенного обозначения образа по схеме: Ф (Г) [А], где Ф – геометрический образ (Г.О.); (Г) – геометрическая часть (перечень

фигур, участвующих в образовании геометрического образа); [А] – закон

5

образования данного образа (указывает на взаимосвязь между фигурами участвующих в образовании этого геометрического образа).

1 Метод проекций. Виды проецирования

Для построения изображения геометрических образов на плоскости пользуются методом проецирования.

Проекция – это отображение геометрического образа на плоскость проекций, полученное при помощи аппарата центрального или параллельного проецирования.

Пример центрального проецирования (рисунок 1):

1)точка S – центр проецирования;

2)плоскость П1 – плоскость проекции, не проходящая через S.

3)точка А - геометрический образ.

Проводим через S и A прямую, которая называется проецирующей, до пересечения с плоскостью П1, найдем точку А1, которая является проекцией точки А на плоскости П1.

S

А

П1

А1

Рисунок 1 - Центральное проецирование

Пример параллельного проецирования:

1)S - направление проецирования (S – удалена в бесконечность);

2)П1 - плоскость проекции;

3)А и В – геометрические образы.

6

При параллельном проецировании проецирующие линии (лучи) составляют с плоскостью проекций один и тот же угол. Если направление S и, следовательно, проецирующие линии перпендикулярны плоскости проекции, то способ проецирования называется прямоугольным, а полученные проекции прямоугольными или ортогональными.

В А

S

α

В1 α

А1

П1

Рисунок 2 - Параллельное проецирование

Одна проекция объекта проецирования (точки, прямой, плоскости или поверхности) не определяет его положения в пространстве, для определения положения объекта необходимо иметь не менее двух его проекций. С этой целью строят прямоугольные проекции геометрических образов на две или три взаимно перпендикулярные плоскости проекций. Прямоугольный метод проецирования на две или три взаимно перпендикулярные плоскости является основным методом начертательной геометрии. По этому методу изготовляются все технические чертежи.

7

2 Инвариантные свойства ортогонального (прямоугольного) проецирования

При параллельном ортогональном проецировании, в общем случае, нарушается метрическое равенство между оригиналом и его проекцией, хотя проекция сохраняет некоторые свойства оригинала, которые называются инвариантными (неизменяемыми):

1. Проекция точки есть точка:

А→Ап

2.Проекция прямой на плоскость есть прямая:

L(AB)→Lп(AпBп)

3.Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии:

А L Aп Lп

4.Проекции взаимно прямых также взаимно , а отношение отрезков таких прямых равно отношению их проекций.

II L IABII ICDI		ICDI IC D I
MIIL M n n			=	n	n
				n	n

5.Точка пересечения, проекций пересекающихся прямых является проекцией точки пересечения этих прямых:

а∩b=M aп∩bп=Мп

6.Плоская фигура, параллельная плоскости проекции проецируется на эту плоскость без искажений.

7.Плоский прямоугольник в общем случае проецируется в многоугольник с тем же числом вершин. Если плоскость многоугольника параллельна направлению проецирования, то она проецируется в прямую линию.

8.Параллельный перенос оригинала или плоскости проекций не изменяет вида и размеров проекций оригинала.

8

9.Если хотя бы одна из сторон прямого угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол проецируется без искажений.

3 Точка

Прямоугольной проекцией точки на плоскость называется основание перпендикуляра, опущенного из точки на плоскость проекции.

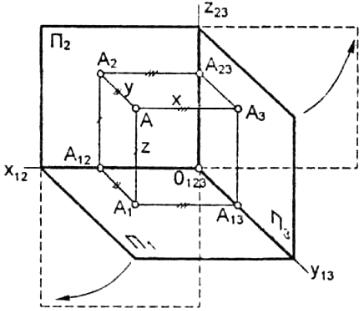
В качестве плоскостей проекций возьмем три взаимно перпендикулярные плоскости П1, П2, П3 (Рисунок 3).

Плоскость П1, называется горизонтальной плоскостью проекций; плоскость П2 – фронтальной плоскостью проекций; плоскость П3 – профильной плоскостью проекций.

X, Y, Z – оси проекций; О – начало координат. Проецирующие линии: АА1 П1, АА2 П2, АА3 П3.

Рисунок 3 – Проецирование точки А на 3 плоскости проекций

9

Остальные линии чертежа называются линиями связей проекций. Название проекций точки А: А1 – горизонтальная проекция; А2 –

фронтальная проекция; А3 – профильная проекция.

Для получения комплексного чертежа следует совместить плоскости П1 и П3 с плоскостью П2, вращая их вокруг соответствующих осей. При этом следует убрать из пространственной модели точку А и проецирующие лучи, а оставить только линии связи.

	Z23
П2			П3
А2	А23	А3
А12	О12	А13	У3
Х12
		А0
А1
	А13
П1	У1		К0
Рисунок 4 - Комплексный чертеж точки

Комплексным чертежом (рисунок 4) называется чертеж, составленный из комплекса проекций точки, связанных между собой. Для удобства решения задач в дальнейшем поля проекций П1, П2, П3 ограничиваться не будут.

Ось X на комплексном чертеже обозначается X12, так как она принадлежит одновременно двум плоскостям проекции: П1 и П2. Ось Z обозначается Z23, т.к. она принадлежит П2 и П3. Ось Y на П1 обозначается Y1, на П3 – Y3. Центр координат на комплексном чертеже обозначается О123.

10