1.2.2. Геометрическое определение вероятности

Если пространство элементарных событий содержит бесконечное число элементарных событий, то классическое определение вероятности неприменимо. В тех случаях, когда пространство элементарных событий может быть представлено некоторой областью на прямой, плоскости или в пространстве, то, учитывая равную возможность исходов эксперимента, можно построить геометрическое определение вероятности события. Допустим, что пространство элементарных событий можно геометрически представить на плоскости некоторой областью , а любое событие A – подмножеством этой области . Обозначим S() меру области , S(A) – мера области A. Тогда вероятность события A можно определить как отношение соответствующей меры S(A) к мере всей области :

p(A) = . (1.2)

В этом случае выполняются все аксиомы теории вероятности. Следует заметить, что событиями в этом примере считаются множества, для которых может быть определена их площадь.

Пример 1.9. Производится один выстрел по круглой мишени радиуса R. Предполагается, что каждая точка мишени может быть поражена с одинаковой вероятностью. Найти вероятность того, что расстояние от точки попадания до центра мишени меньше r (r<R).

Решение. Обозначим событие A ={точка попадания лежит в заданном круге радиуса r}.Тогда вероятность этого события по формуле (1.2) будет равна

p(A) = .

3. Вычисление вероятности события через элементы комбинаторного анализа

Использование методов комбинаторного анализа широко описано в учебном пособии по теории вероятностей. В данной работе рассмотрим гипергеометрический способ вычисления вероятности события.

Пример 1.10. В урне имеется N шаров, из них M белых и N-M черных. Наудачу из урны извлекают n шаров. Найти вероятность того, что среди них будет ровно m белых шаров.

Решение. Обозначим искомое событие A: A= {выбрано ровно m белых шаров}. Из генеральной совокупности N шаров выбирают без учета порядка следования n шаров. Следовательно, число различных выборок будет равно числу сочетаний из N по n -- . Теперь найдем число выборок объемаn, в которых ровно m белых шаров. Для этого будем выбирать из всех M белых шаров ровно m шаров. Всего число таких различных выборок объема m будет равно числу сочетаний из M по m - . Аналогично, число различных выборок из всех черных шаров поn-m шаров, будет равно числу сочетаний из N-M по (n – m), т.е. . Объединяя каждую выборку изm белых шаров с каждой выборкой из (n – m) черных шаров, получаем искомое число выборок объема n, в которых будет ровно m белых, - . Из классического определения вероятности следует, что

Р(A)= ,

где С_r^k - число сочетаний из r по k, вычисляемое по формуле

, k! = и 0! = 1.

Пример 1.11. Среди десяти изделий находится три бракованных. Выбирают наугад четыре изделия. Определить вероятности следующих событий:

A = {среди выбранных изделий нет бракованных };

B = {из выбранных изделий ровно два бракованных}.

Решение. Определим общее число способов выбора четырех деталей из десяти.

.

Число выборок, благоприятствующих событию A, будет равно

.

Тогда вероятность события A будет равна

p(A)= .

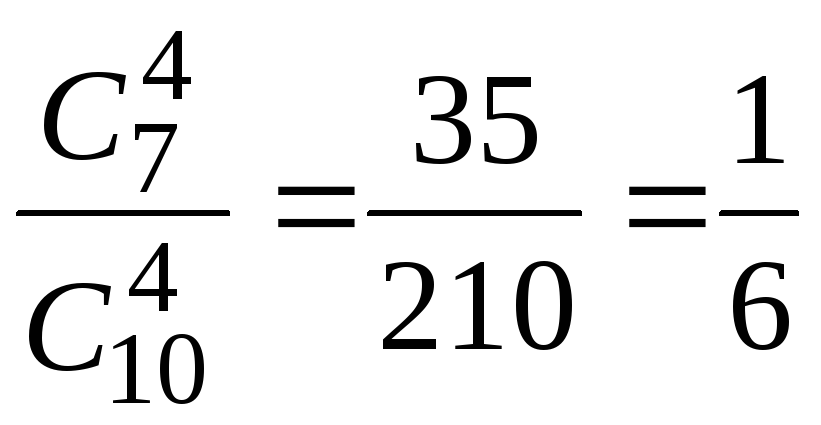Для вычисления вероятности события В применим гипергеометрическое определение. Будем считать изделия шарами, бракованные изделия - белыми шарами, а небракованные изделия - черными шарами. Тогда найти вероятность события B означает найти вероятность того, что среди 4 наугад выбранных шаров будет два белых:

p(B)= =.