2.2.2. Дисперсия случайной величины

Из определения математического ожидания следует, что оно определяет среднее значение случайной величины. Дисперсия характеризует среднюю величину отклонения значений случайной величины от математического ожидания.

Пусть  обозначает дискретную или абсолютно непрерывную случайную величину.

Определение. Моментом второго порядка случайной величины  называется математическое ожидание квадрата этой случайной величины, т. е. число M(²).

Пусть в формулах (2.18) и (2.19) функция g(x)=x². Тогда для моментов второго порядка случайной величины  имеют место формулы

, (2.21)

. (2.22)

Величина -M() определяет отклонение случайной величины  от математического ожидания M().

Определение. Дисперсией случайной величины  называется момент второго порядка случайной величины ( - M()). Дисперсию обозначают D(). Таким образом, дисперсия случайной величины  определяется формулой

D()=M[(- M())²] . (2.23)

Стандартным или средним квадратическим отклонением называют величину, равную квадратному корню из дисперсии и обозначают :=.

Из равенств (2.18), (2.19) для моментов второго порядка следуют формулы для вычисления дисперсии дискретной и абсолютно непрерывной случайных величин соответственно

(2.24)

(2.25)

Дисперсия не существует, если ряд (2.24) или несобственный интеграл (2.25) расходятся.

Свойства дисперсии

1. Для любой случайной величины  выполняется неравенство D() ≥ 0.

2. При умножении случайной величины  на постоянное число С дисперсия умножается на квадрат этого числа, т.е. справедливо равенство

D(C)=C²D().

3. Справедлива следующая формула для вычисления дисперсии

D()=M(²)- M²() , (2.26)

то есть дисперсия случайной величины равна разности второго момента этой величины и квадрата математического ожидания этой же величины.

4. Если случайные величины  и  независимы, дисперсия их алгебраической суммы равна сумме дисперсий, т.е.

D(+)=D()+D(). (2.27)

5. Дисперсия постоянной величины С равна нулю.

Пусть  обозначает дискретную случайную величину с рядом распределения

x_i x₁ x₂ , …, x_n…

p_i p₁ p₂ , …, p_n… .

В этом случае согласно свойству 3 дисперсия вычисляется по формуле

D()=.(2.28)

2.2.3. Нормальное распределение случайной величины

Нормальное распределение часто используется для описания случайных явлений, в которых на результат измерения влияет большое число независимых случайных факторов.

Определение. Случайная величина ξ имеет нормальное или гауссовское распределение, если ее плотность распределения вероятностей при всех x задается равенством 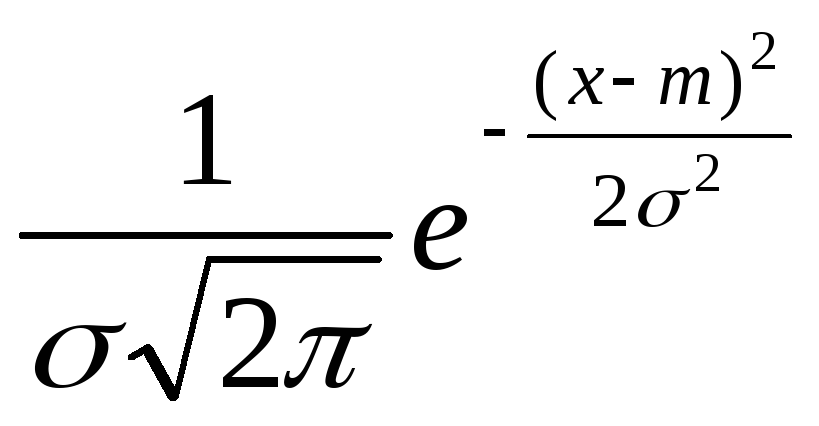. (2.29)

Числаm и σ называются параметрами распределения: параметр m может быть любым действительным числом: -∞ < m < +∞, а параметр σ – положительным: σ>0. Символическая запись означает, что cлучайная величина ξ имеет нормальное распределение с параметрамиm и σ².

y

F(x)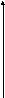

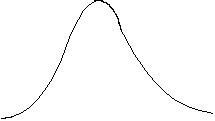
Отметим некоторые свойства графика этой функции (кривой нормального распределения).

Во-первых, функция принимает максимальное значениеприx=m.

Во-вторых, функция симметрична относительно вертикальной прямойx=m.

В-третьих, асимптотой кривой нормального распределения является ось Ох. Особую роль играет нормальное распределение с параметрами m=0, σ=1, которое часто называют стандартным (или нормированным) нормальным распределением.

Плотность стандартного нормального распределения имеет вид

,(2.30)Ниже приведен график y = f₀(x).

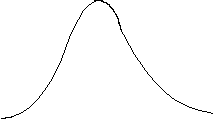
Функция распределения случайной величины, имеющей нормальный закон, может быть представлена в виде несобственного интеграла

F(x) =. (2.31)

Функцию распределения стандартного нормальногозакона

Ф(х) = (2.32)

часто называют функцией Лапласа, для которой имеются таблицы значений, широко используемые в статистических исследованиях. Рассмотрим свойства нормального распределения.

Свойство 1. Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ, т.е. . Тогда математическое ожидание равно параметруm, а дисперсия равна σ² , т.е.

M(ξ)=m; D(ξ)= σ².

Свойство 2. Между функциями распределения F(x) и имеет место следующее соотношение

. (2.33)

Таблицы значений функции не содержат значений при x<0. В таких случаях можно использовать следующее свойство.

Свойство 3. При любых значениях x имеет место равенство

. (2.34)

Следующее свойство позволяет вычислить вероятность попадания случайной величины в интервал, используя таблицы значений функции .

Свойство 4. Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ, т.е. . Тогда вероятность попадания случайной величиныξ в интервал [a,b] можно найти по формуле

. (2.35)

В частности, для симметричного интервала относительно m имеет место формула для любого :

. (2.36)

Формула (2.36) непосредственно следует из (2.35), в которой надо положить и использовать свойство, что .Тогда получим

.

Свойство 5 (закон трех сигм). Пусть случайная величина ξ имеет нормальное распределение с параметрами m и σ, т.е. . Тогда с вероятностью больше 0,99 значения случайной величины содержатся в интервале

Действительно, по свойству 4, . Из таблицы функцийнаходим значение=0,9987. Отсюда следует, что