гидравлика 24-28
.pdf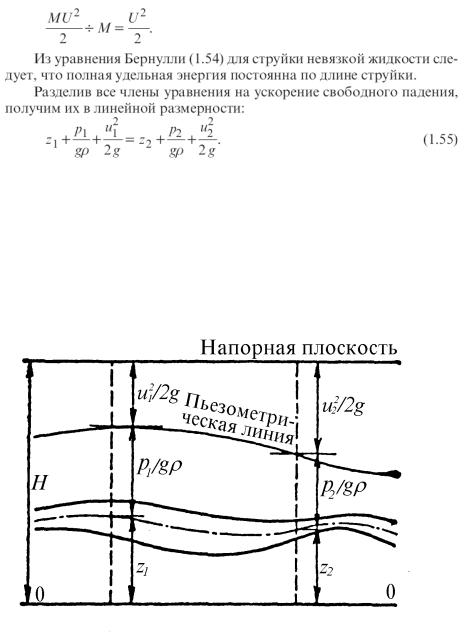
24. Пьезометр и пьезометрическая высота. Трубка Пито.
Интерпретация уравнения Бернулли для установившегося движения
Уравнение Бернулли можно интерпретировать с различных позиций: с геометрической и энергетической.
Положение рассматриваемой частицы жидкости определяется вертикальной координатой z. Величина gz выражает потенциальную энергию жидкости массой M = 1, поднятой от плоскости 00 на высоту z, т.е. gz - удельная (отнесенная к массе) потенциальная энергия положения. Величина p/ρ выражает удельную (отнесенную к массе) потенциальную энергию давления. Энергетический смысл первых двух членов уравнения Бернулли таков же, как и в гидростатике: gz + p/ρ - удельная потенциальная энергия жидкости.
Третий член u2/2 представляет собой кинетическую энергию жидкости массой
M = 1 (удельную кинетическую энергию), так как:
Отметим, что в такой записи члены уравнения (1.55) выражают удельную энергию, отнесенную к весу (Mg = G).
Как и в гидростатике, величину z называют высотой положения, а величину p/gρ - пьезометрической высотой. Сумма первых двух членов уравнения
(1.54) z + p/gρ - пьезометрический напор. Третий член уравнения u2/2g
линейная величина. Как известно, начавшаяся двигаться вертикально со скоростью u при отсутствии сопротивления движению, поднялась бы на высоту u2/2g. Этот член уравнения Бернулли называется скоростной высотой или скоростным напором. Все члены уравнения Бернулли можно изобразить графически (рис.1.25).
Рис. 1.25. Графическое изображение составляющих уравнения Бернулли
Если откладывать вертикально от произвольной горизонтальной плоскости высоты z1 и z2 (до рассматриваемых точек), а затем пьезометрические высоты p1/gρ и p2/gρ, скоростные высоты u12/2g и u22/2 g,
то для невязкой жидкости концы сумм отрезков z1 + p1/gρ + u12 /2g и z2 + p2/gρ + u22/2g расположатся на горизонтальной линии, называемой напорной линией. Концы отрезков z + p/gρ соединены пьезометрической линией.
Пьезометрическим уклоном называется отношение:
где l – расстояние между двумя сечениями.
Сумму трех высот называют гидродинамическим напором Н. Из уравнения Бернулли (1.55) для струйки невязкой жидкости следует, что гидродинамический напор постоянен по длине струйки.
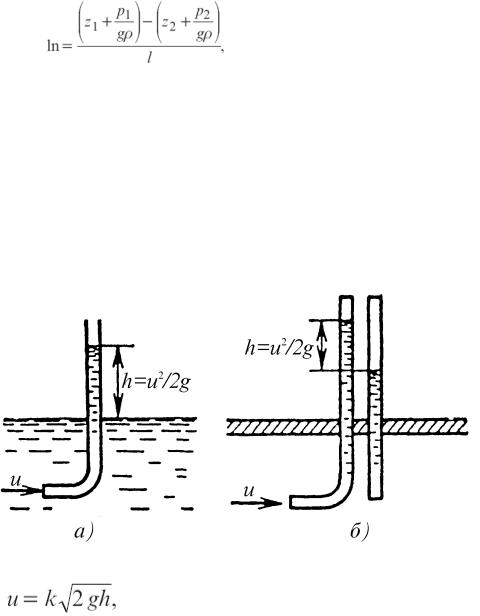
Если при плавно изменяющемся безнапорном движении опустить в поток так называемую трубку Пито–трубку, нижний конец которой изогнут под прямым углом навстречу потоку, то вода в трубке поднимется над свободной поверхностью, где давление равно атмосферному, на высоту h = u2/2g
(рис.1.26а).
При определении местных скоростей в напорном потоке применяется система из двух трубок, одна из которых представляет собой обычный пьезометр, показывающий пьезометрический напор p/g, а другая, только что описанная, измеряет величину напора z + p/gρ + u2 /2g (рис.1.26, б). Разность уровней в обеих трубках h представляет собой скоростной напор u2 /2g.
Рис. 1.26. Трубка Пито Местные скорости определяются с помощью трубки Пито по формуле:
где k - поправочный коэффициент, определяемый для каждой трубки опытным путем.
Уравнение Бернулли для идеальной жидкости
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).
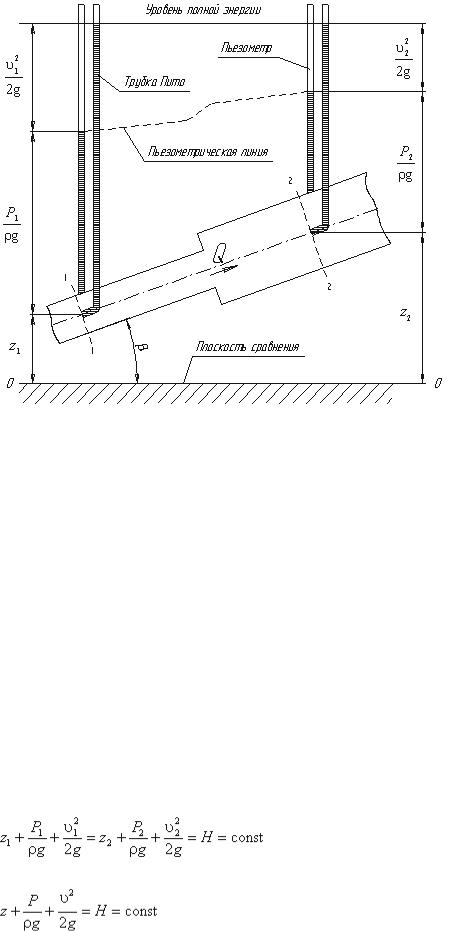
Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры - тонкостенные
стеклянные трубки, в которых жидкость поднимается на высоту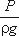 
. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни,
если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
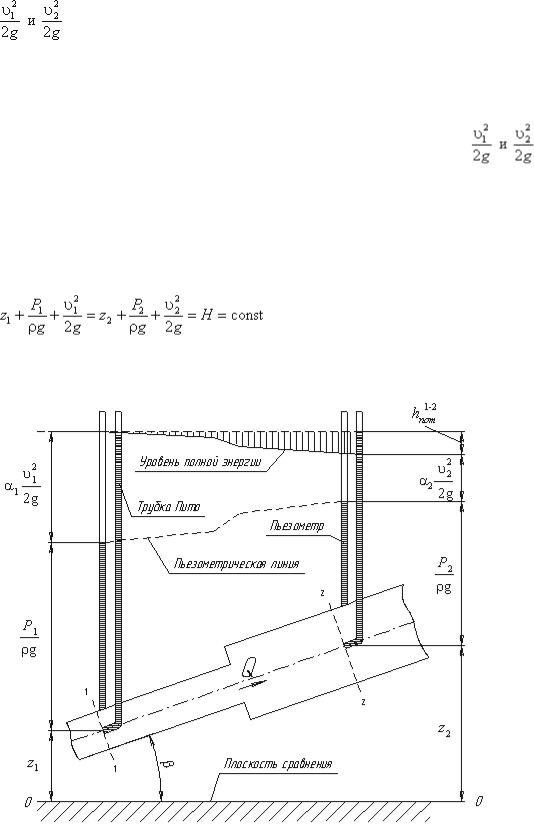
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
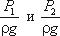- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
- удельные кинетические энергии в тех же сечениях. Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 - геометрические высоты сечений 1-1 и 2-2 над
плоскостью сравнения;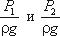 
- пьезометрические высоты; - скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для реальной жидкости
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости
Потерянная энергия или потерянный напор обозначаются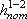 
и имеют также линейную размерность.
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).
Потерянная высота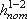 
складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)
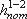= hлин + hмест
С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ1ω 1 = υ2ω2.
25. Основное уравнение равномерного установившегося движения
Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потери напора определяются лишь потерями по длине.
Выделим из потока участок жидкости длиной l и запишем уравнение Бернулли для сечений 1 и 2( рис. 32 )
Рис. 38
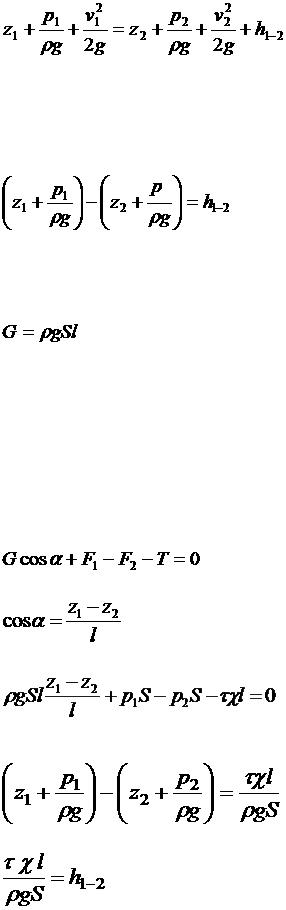
где
z1 , z2 - ординаты центра тяжести сечений 1,2,
p1 , p2 - давление в центрах тяжести этих сечений, v1 , v2 - средние скорости в этих сечениях,
h1-2 - потери напора по длине.
Так как движение равномерное, то v1 =v2 и уравнение можно переписать так:
. |
(1) |
В случае равномерного движения разность удельных потенциальных энергий равна потере напора по длине.
Для вычисления этой разности напишем сумму проекций на ось А-А всех сил, действующих на участке 1-2. Эти силы следующие:
1) сила тяжести жидкости
,
2) силы давления на плоские сечения
, 
, 
,
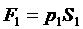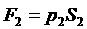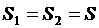3) сила трения
,
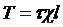где t - сила трения на единицу площади смачиваемой поверхности русла, c - смоченный периметр,
4) силы давления стенок на жидкость ( эти силы не подсчитываем, так как они параллельны оси А-А и, следовательно, их проекции на ось А-А равны нулю ).
Спроектируем все эти силы на ось А-А:
.
Из рисунка
.
Подставим выражение для сил в уравнение
.
Разделим обе части этого равенства на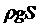 
, имеем
. (2)
Сравнивая выражения (1) и (2), находим
,
откуда
.
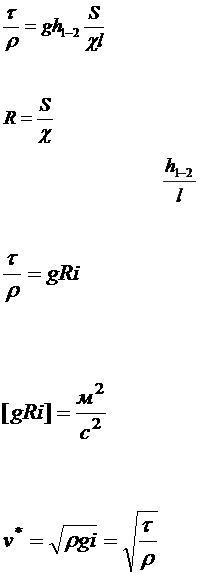
Отношение площади живого сечения S к смоченному периметру c называется
гидравлическим радиусом
.
Величина |
обозначается через i и называется гидравлическим |
уклоном.
Получаем
.
Это уравнение называется основным уравнением равномерного
движения.
Величина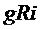 
имеет размерность квадрата скорости
.
Выражение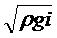
- называется динамической скоростью,
обозначается v*
.
26. Режимы движения жидкости
Ламинарный и турбулентный режимы движения жидкости
Многочисленные экспериментальные исследования гидравлических сопротивлений показывают, что потери удельной энергии при движении существенно зависят от того, какой режим движения наблюдается в потоке - ламинарный или турбулентный. Существование того или иного режима движения определяется поведением частиц жидкости.
Наглядное представление о характерных признаках ламинарного и турбулентного режимов движения можно получить, если провести исследования этих режимов на опытной установке, (установка Рейнольдса)схематически изображенной на рис.1.30.
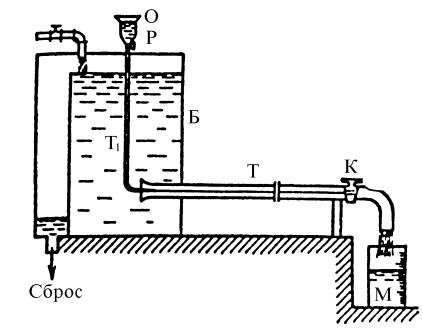
В состав установки входит бак Б, наполненный исследуемой жидкостью, присоединенная в нижней части бака стеклянная (или выполненная из какоголибо другого прозрачного материала) труба Т с плавным входом и размещенный над большим баком маленький бачок О, наполненный окрашенной жидкостью (раствором краски) с плотностью, близкойк плотности жидкостивбаке Б. Отбачка отходит тонкая трубкаT1, входящая в трубу Т. Трубы Т иT1 снабжены для регулирования расхода жидкости и краски кранами К и Р соответственно. Исследуемая жидкость из трубы Т сливается во время опыта в мерный сосуд М.
При неизменном диаметре трубы Т в зависимости от величины средней скорости движения жидкости имеет различные характерные особенности. При малых скоростях струйка краски движется, не смешиваясь с остальными слоями жидкости (рис.1.31а). Если пустить несколько подкрашенных струек, то они также будут двигаться, не перемешиваясь между собой и не смешиваясь с остальной массой жидкости. Линии тока в трубе при этом устойчиво прямолинейны.
При несколько увеличенном расходе и, следовательно, увеличивающейся средней скорости окрашенная струйка искривляется. Струйка начинает пульсировать (колебаться в пространстве), что свидетельствует о наличии непрерывных изменений (пульсаций) скорости во времени в различных точках. При дальнейшем увеличении скорости и увеличении пульсации окрашенная струйка распадается, перемешиваясь с остальной массой жидкости, при этом наблюдаются заметные завихрения по всему сечению трубы (рис.1.31б). Режим движения, при котором отсутствуют пульсации скорости и перемешивание частиц, называется ламинарным (от латинского слова lamina слой) режимом движения.
Режим движения, характерной особенностью которого является перемешивание частиц и пульсации скорости, называется турбулентным (от латинского слова turbulentus беспорядочный) режимом движения.
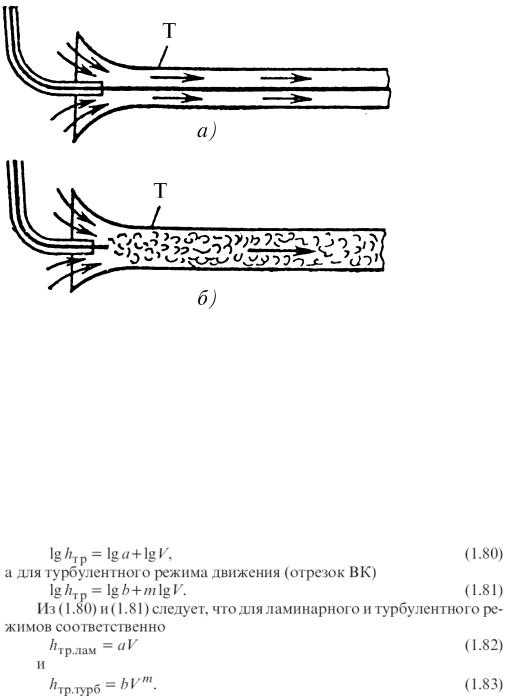
Рис. 1.31. Характерные особенности ламинарного (а) и турбулентного (б) режимов движения жидкости Ламинарный режим движения встречается чаще всего при движении по трубам
жидкостей с большой вязкостью (нефти, нефтепродуктов и т.д.), а также при движении воды в тонких капиллярных трубках и порах грунта.
Турбулентный режим встречается в большинстве случаев гидротехнической и гидромелиоративной практики (движение воды в трубах, каналах, реках и т.п.).
Многочисленные экспериментальные данные подтверждают, что при разных режимах движения жидкости потери энергии по разному зависят от скорости движения.
Если полученные из опытов потери напора hтр и среднюю скорость изобразить на логарифмическом графике (рис.1.32), то для ламинарного режима (отрезок АК) можно записать:
Рис. 1.32. Логарифмический график зависимости потерь напора hтр от средней скорости V для ламинарного и турбулентного режимов движения жидкости
Коэффициент m перед lgV является тангенсом угла наклона данного отрезка по отношению к оси абсцисс. При ламинарном режиме движения m = 1, а при турбулентном режиме движения m = 1,75 - 2,0.
Таким образом, потери удельной энергии (напора) по длине при ламинарном режиме движения пропорциональны средней скорости в первой степени, а при турбулентном режиме средней скорости в степени выше первой, изменяющейся от 1,75 до 2,0.
27. Потери напора по длине. Формула Вейсбаха-Дарси.
Формула Вейсбаха[1] в гидравлике — эмпирическая формула, определяющая потери напора или потери давления при развитом турбулентном течении несжимаемой жидкости на гидравлических сопротивлениях (предложена Юлиусом Вейсбахом в 1855 году):
где
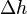— потери напора на гидравлическом сопротивлении;
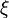— коэффициент местного сопротивления;
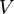— средняя скорость течения жидкости;
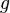— ускорение свободного падения;
величина называется скоростным (или динамическим) напором. Формула Вейсбаха, определяющая потери давления на гидравлических сопротивлениях, имеет вид:
где