2 семестр / ПОСОБИЕ_ВычМат

Министерство образования Республики Беларусь

УО МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРОДОВОЛЬСТВИЯ

Кафедра информатики и вычислительной техники

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА И РАСЧЕТЫ НА ЭВМ

Методическое пособие для студентов специальности

36 09 01 – Машины и аппараты пищевых производств

36 20 01 – Низкотемпературная техника дневной и заочной формы обучения

Могилев 2004

2

УДК 519.61

Рассмотрено и утверждено на заседании кафедры

«Информатика и вычислительная техника» Протокол № 13 от «13» мая 2004 г.

Составители: зав. кафедрой ИВТ, к.ф.-м.н. Г.Н. Воробьев ассистент И.П.Овсянникова

Рецензент

к.ф.-м.н., доцент Гальмак А.М.

© Могилевский государственный университет продовольствия

3
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ......................................................................................................................	5
1 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ ..............................................	6
1.2 Методы отделения корней ........................................................................................	6
1.2.1 Постановка задачи ..................................................................................................	6
1.2.2 Табличный метод отделения корней ....................................................................	6
1.2.3 Графический метод отделения корней.................................................................	7
1.2.4 Метод интервалов отделения корней ...................................................................	7
1.2 Методы уточнения приближенных корней.............................................................	8
1.2.1 Постановка задачи ..................................................................................................	8
1.2.2 Оценка погрешности приближенного корня .......................................................	8
1.2.3 Метод половинного деления .................................................................................	9
1.2.3.1 Алгоритм метода половинного деления..........................................................	10
1.2.4 Метод итераций ....................................................................................................	11
1.2.4.1 Алгоритм метода итераций...............................................................................	15
1.2.5 Метод Ньютона.....................................................................................................	15
1.2.5.1 Алгоритм метода Ньютона ...............................................................................	17
1.2.6 Метод хорд ............................................................................................................	17
1.2.6.1 Алгоритм метода хорд.......................................................................................	18
1.2.7 Комбинированный метод.....................................................................................	19
1.2.7.1 Алгоритм комбинированного метода..............................................................	19
1.2.8 Программы уточнения корней уравнений .........................................................	20
1.2.8.1 Метод половинного деления ............................................................................	20
1.2.8.2 Метод итераций .................................................................................................	21
1.2.8.3 Метод Ньютона..................................................................................................	21
1.2.8.4 Метод хорд .........................................................................................................	22
1.2.8.5 Комбинированный метод..................................................................................	23
1.2.9 Уточнение корней уравнений средствами Excel...............................................	24
1.2.9.1 Метод половинного деления ............................................................................	25
1.2.9.2 Метод итераций .................................................................................................	26
1.2.9.3 Метод Ньютона..................................................................................................	26
1.2.9.4 Метод хорд .........................................................................................................	27
1.2.9.5 Комбинированный метод..................................................................................	28
1.2.9.6 Использование команды "Подбор параметра" ...............................................	29
1.2.10 Решение уравнений средствами MathCAD......................................................	29
2. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ ..............................................	30
2.1 Постановка задачи ...................................................................................................	30
2.2 Метод Гаусса............................................................................................................	30
2.2.1 Алгоритм метода Гаусса ......................................................................................	32
2.2.2 Программа решения системы линейных уравнений методом Гаусса.............	33
2.3 Решение систем линейных уравнений методом простой итерации..................	34
2.3.1 Алгоритм метода итераций..................................................................................	36
2.3.2 Программа решения системы линейных уравнений методом итераций........	37
2.4 Решение систем линейных уравнений средствами Excel....................................	38
2.5 Решение систем линейных уравнений средствами MathCAD ............................	40
3 МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ................................................................	42
3.1 Понятие о приближении функций .........................................................................	42

	4
3.2	Интерполирование функций...................................................................................	42
3.2.1 Интерполяционная формула Лагранжа..............................................................		42
3.2.2 Интерполяционные формулы Ньютона .............................................................		44
3.2.2.1 Алгоритмы интерполирования многочленами Ньютона...............................		47
3.2.3 Интерполирование функций средствами MachCAD ........................................		49
3.3	Аппроксимация функций........................................................................................	51
3.3.1 Оценка точности аппроксимации .......................................................................		52
3.3.2 Алгоритм и программа аппроксимации функции.............................................		53
3.3.2.1 Решение в системе Turbo Pascal.......................................................................		54
4 ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ..............................................................		57
4.1	Вычисление производной по ее определению......................................................	57
4.2	Конечно-разностные аппроксимации производных ............................................	58
4.3	Другие методы вычисления производных первого и второго порядков ...........	59
4.3.1 Алгоритм вычисления первой и второй производной функции......................		60
4.3.2 Программа на языке Turbo Pascal для вычисления первой и второй
производной функции ...................................................................................................		61

4.3.3 Вычисления первой и второй производной функции средствами MS Excel .62

5 ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ........................................................................		63
5.1	Квадратурная формула прямоугольников.............................................................	63
5.2	Квадратурная формула трапеций...........................................................................	64
5.3	Квадратурная формула парабол (Симпсона) ........................................................	65
5.4	Оценка погрешностей квадратурных формул ......................................................	67
5.5	Метод двойного пересчета......................................................................................	68
5.6	Алгоритм вычисления интегралов по формулам прямоугольников, трапеций и
Симпсона ........................................................................................................................		68
5.7	Программа на языке Turbo Pascal для вычисления интегралов по формулам
прямоугольников, трапеций и Симпсона....................................................................		69
5.8	Вычисление интегралов по формулам прямоугольников, трапеций и парабол
средствами MS Excel .....................................................................................................		70
5.9	Вычисление интегралов средствами MachCAD...................................................	71
6 ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ..................		72
6.1 Задача Коши .............................................................................................................		72
6.2	Метод Рунге-Кутта для решения дифференциальных уравнений .....................	72
6.3	Алгоритм решения задачи Коши методом Рунге-Кутта .....................................	73
6.4	Программа на языке Turbo Pascal для решения задачи Коши методом Рунге-
Кутта................................................................................................................................		73
6.5	Решение задачи Коши методом Рунге-Кутта средствами MS Excel..................	74
6.6	Решение задачи Коши средствами MachCAD .....................................................	76
Рекомендуемая литература ...........................................................................................		78
ПРИЛОЖЕНИЕ А..........................................................................................................		79
ПРИЛОЖЕНИЕ Б ..........................................................................................................		80
ПРИЛОЖЕНИЕ В..........................................................................................................		82
ПРИЛОЖЕНИЕ Г ..........................................................................................................		84
ПРИЛОЖЕНИЕ Д..........................................................................................................		85
ПРИЛОЖЕНИЕ Е ..........................................................................................................		86

5

ВВЕДЕНИЕ

Созданные системы компьютерной математики значительно облегчают выполнение различных математических расчетов. Последние версии систем содержат тщательно сбалансированные средства численных и символьных вычислений с графической визуализацией результатов в сочетании с самым современным интерфейсом пользователя, мощной справочной системой, общими пакетами расширения. Все, что они делают за нас – это точно и красиво. Что же остается нам? Нам остается лишь правильно сформулировать проблему и проверить корректность ее решения. Эта, далеко не элементарная задача, требует от инженеров знаний возможностей различных вычислительных систем общего и специального назначения. Рассмотрение примеров без знания теоретических моментов, как правило, не способствует разрешению этих порой весьма непростых вопросов. И здесь на помощь приходит вычислительная математика со стройной системой численных методов. Знание основ вычислительной математики и применение этих знаний к решению различных задач – путь к разрешению поставленных задач.

Это пособие призвано помочь студентам самых различных специальностей освоить классические методы вычислительной математики. Наряду с методами и алгоритмами рассматриваются конкретные их реализации, в частности, в среде программирования Turbo Pascal, в электронной таблице Excel, системе MathCAD. Рассмотрение конкретных методов продиктовано требованиями учебной программы по дисциплине "Вычислительная математика, программирование и расчеты на ЭВМ" для студентов специальностей 36 09 01 – Машины и аппараты пищевых производств, 36 20 01 – Низкотемпературная техника. Пособие включает в себя численные методы решения уравнений, решение систем линейных уравнений, методы приближения функций, численное дифференцирование и интегрирование, численное решение дифференциальных уравнений. Примеры, которые приведены в пособии, окажут существенную помощь студентам в решении различных задач с использованием современных информационных технологий, в частности, с использованием системы программирования Turbo Pascal, электронной таблицы Excel, системы компьютерной математики MathCAD.

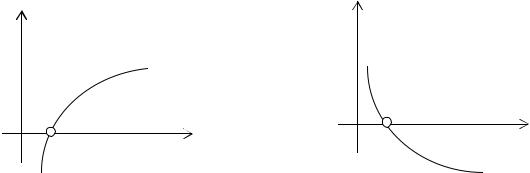
6

1 ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ

1.2Методы отделения корней

1.2.1Постановка задачи

Пусть

f(x)= 0

(1)

– некоторое уравнение. Число x называется корнем или решением данного уравнения, если оно, будучи подставлено в уравнение, обращает его в равенство, т. е. f(x) = 0. Число x называют нулем функции y = f(x).

Выделение из области определения функции f(x) отрезков [ai; bi], в каждом из которых содержится один и только один корень xi уравнения f(x) = 0, называют

отделением корней уравнений.

Достаточные условия существования корней на заданном интервале (a; b) дает следующая теорема.

Теорема 1. Если непрерывная функция f(x) принимает значения разных зна- ков на концах отрезка [a; b], то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x) = 0, т. е. найдется хотя бы одно число x Î (a; b) такое, что f(x) = 0.

Корень x заведомо будет единственным, если производная f ¢(x) существует и сохраняет постоянный знак внутри интервала (a; b) (см. рис. 1).

y

y

α							β
								x
				x	α ξ
	ξ	β
		f ′(x) > 0					f ′(x) < 0
					Рис. 1

1.2.2 Табличный метод отделения корней

Табличный метод отделения корней состоит в том, что составляют таблицу

значений функции y = f(x) в ряде промежуточных точек x = a1, a2, ...,ak, ak+1, ..., an, выбор которых учитывает особенности функции f(x). Если окажется, что

f(ak)×f(ak+1) < 0, то в силу теоремы 1 в интервале (ak; ak+1) имеется корень xk уравнения f(x) = 0. Этот корень единственный, если производная функции сохраняет

знак на интервале (ak; ak+1).

7

1.2.3 Графический метод отделения корней

Графический метод отделения корней состоит в том, что действительные корни уравнения f(x) = 0 приблизительно можно определить как абсциссы точек пересечения графика функции y = f(x) с осью Ох. Если уравнение (1) не имеет близких между собой корней, то этим способом его корни легко отделяются. На практике часто бывает выгодно уравнение (1) заменить равносильным ему уравнением ϕ(x) = ψ(x), где функции ϕ(x) и ψ(x) более простые, чем функция f(x). Тогда, построив графики функций y = ϕ(x) и y = ψ(x), искомые корни получим как абсциссы точек пересечения этих графиков.

Замечание. Графический метод отделения корней, выполненный на компьютере, не гарантирует успешный поиск всех корней на заданном интервале, так как из-за особенностей реализации график не будет соответствовать действительному графику функции f(x).

1.2.4 Метод интервалов отделения корней

Метод интервалов отделения корней состоит в том, чтобы найти интервал [α; β] таким образом, что f(α) и f(β) имеют различные знаки. Как только будет найден такой интервал, величина которого не имеет значения, то согласно теореме 1, там будет содержаться корень уравнения f(x) = 0. Но теорема 1 не гарантирует, что этот корень будет единственным. Корень будет заведомо один, если интервал [α; β] является интервалом знакопостоянства производной, поэтому рекомендуется следующая схема:

−найти производную f ′(x) функции f(x);

−найти критические точки функции f(x);

−составить таблицу знаков функции на границах отрезка [α; β] и в критических точках;

−определить отрезки, на концах которых функция принимает значения противоположных знаков.

Указанная схема достаточна сложна в практической реализации. Обычно ин-

тервал делят на n частей точками α = x0 < x1 < …< xn = β и вычисляют значения

функции yk = f(xk). Если f(x) непрерывна и две смежные точки (xk–1, yk–1), (xk, yk) лежат по различные стороны оси x, то согласно теореме 1, по крайней мере, один

корень лежит на интервале [xk–1, xk]. Но если существует корень, и две смежные точки лежат по одну сторону оси x, то теорема 1 не применима. Это возможно в ситуации близко расположенных корней либо сливающихся корней, т. е. корней, в которых график соприкасается с осью Ox, но не пересекает ее, или корней, сливающихся с вертикальной асимптотой. Ситуация f(xk) ≈ 0 характеризует xk как предварительное приближение корня. Однако график может быть близок к нулю на широком диапазоне значений около точки xk, тогда xk возможно не близка к истинному корню. В связи с этим добавляется требование, чтобы тангенс наклона графика изменял знак вблизи точки (xk, yk). В этом случае xk является приближением к корню. Поэтому рекомендуется следующая схема локализации корня:

вале [xk–1; xk+1].

Замечание. Если f(x) имеет локальный экстремум, чрезвычайно близкий к нулю, то xk в данной схеме будет рассматриваться как приближенное значение корня, когда f(xk) » 0, несмотря на то, что xk возможно и не является приближением к корню. Такие ситуации необходимо рассматривать, когда применяется любой численный алгоритм для нахождения корня.

1.2 Методы уточнения приближенных корней 1.2.1 Постановка задачи

Под уточнением приближенных корней понимают доведение их до заданной степени точности в следующей задаче.

Пусть дано уравнение (1), в котором f(x) – непрерывная функция и задан интервале [a; b] изоляции корня, на концах которого функция f(x) имеет различные знаки, т. е. sgn f(a)×sgn f(b) < 0, где

8

- разбить интервал [a: b] на n частей точками a = x0 < x1 < …< xn = b и вычислить значения функции yk = f(xk) k = 0, 1, …, n;

- если (yk–1)·(yk) = 0, то точка xk–1 или точка xk является нулем функции f(x); - если (yk–1)·(yk) < 0, то корень локализован на интервале [xk–1; xk];

- если (yk–1)·(yk) > 0 и |yk| < e и yk − yk−1 < 0, то корень локализован на интер-

yk +1 - yk

ì 0,если x = 0; sgn x = ïí 1,если x > 0; ïî- 1,если x < 0.

Требуется найти с точностью e приближенное значение корня уравнения (1) на интервале [a; b] изоляции корня.

1.2.2 Оценка погрешности приближенного корня

Оценку погрешности приближенного корня дает следующая теорема.

Теорема 2. Пусть x – точный, а x - приближенный корни уравнения f(x) = 0, находящиеся на одном и том же отрезке [a, b], причем ½f ¢(x )| ³ m1 > 0 при

a £ x £ b. В таком случае справедлива оценка

½ x – x½£			f ( x )			.	(2)
			m
		1

Замечания:

1.В частности, в неравенстве (2) за m1 можно взять наименьшее значение

|f ¢(x)| при a < x < b.

2.Оценка (2) значительно завышена. Каждый из ниже рассматриваемых методов уточнения приближенного корня имеет свою оригинальную оценку.

9

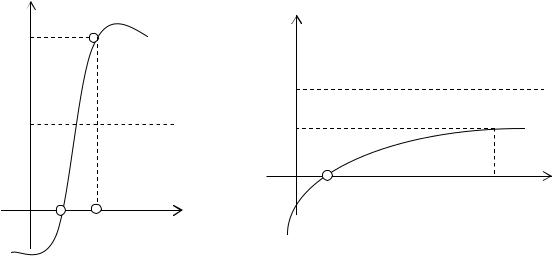
3. Если e>0 – погрешность приближенного корня и |f( x )|< e, то не следует считать, что x является хорошим приближенным точного корня x, и, наоборот, если |f( x )|>e – полагать, что x есть грубое значение точного корня x. Более того, если уравнение f(x) = 0 умножить на произвольное число N ¹ 0, то получается равносильное уравнение Nf(x) = 0, причем число |Nf(x)| можно сделать сколь угодно большим или сколь угодно малым за счет выбора множителя N. На рис. 2 демонстрируется это утверждение.

y				y
				ε
ε
			f ( x )
					ξ				x
							x
ξ			x
	x
|f( x )| >e и |x –			x | < e			|f( x )| < e и |x – x | >e
			Рис. 2

1.2.3 Метод половинного деления

Для нахождения корня уравнения (1), принадлежащего отрезку [a; b], делим этот отрезок пополам. Если

	æ a + b ö
	fç						÷ = 0,
				2
то по определению	è						ø
				æ a + b ö
	x	= ç								÷
							2
является корнем уравнения (1). Если				è						ø
	æ a + b ö
	fç						÷	¹ 0,
				2
то выбираем ту из половин	è						ø
é	a + bù							éa + b
êa;			ú	или				ê
	2									2
ë		û						ë

;bùú ,

û

исходного отрезка, на концах которых функция f(x) имеет противоположные знаки. Новый суженный отрезок [a1; b1] снова делим пополам и проводим то же рас-

10

смотрение. В результате получаем на каком-то этапе или точный корень x уравнения (1) или бесконечную последовательность вложенных друг в друга отрезков

[a1; b1], [a2; b2], ..., [an; bn], ...

таких, что

sgn f(an)× sgn f(bn) < 0

и		1
	bn – an =		(b – a).	(4)
		2n
Число x = liman = limbn является корнем уравнения (1).
n→∞	n→∞

Оценку погрешности на n-м шаге вычисления можно получить из следующих рассуждений: так как и точный корень x и срединная точка xn лежит на интервале [an; bn], то расстояние между ними не может быть больше половины длины этого интервала. Поэтому

|x – xn| £	bn − an			для всех n.
2
Объединив последний результат с результатом (4), получим
|x – xn| £		b − a		для всех n.	(5)
		2n +1
Достоинством метода деления пополам является то, что формула (5)					дает

предопределенную оценку точности вычисляемого решения. Например, если начальная длина интервала изоляции корня равна b – a = 2 и число повторяемых делений пополам равно 31, то в силу (5) ошибка ограничена значением

	2		1	–10
|e31| =		=		» 4,656613×10 .
	232		231

Можно показать, что n повторяемых делений пополам, необходимых для гарантии того, что n-я срединная точка xn является приближением к нулю функции и ошибка приближения меньше, чем наперед заданное значение e, равно

	éln( b - a ) - ln(e )ù
	n = ê		ú	,	(6)
		ln( 2 )
	ë		û

где [ ] – операция взятия целой части числа.

1.2.3.1Алгоритм метода половинного деления

1.Ввести исходные данные: a, b – границы интервала изоляции корня уравнения (1); e – погрешность приближенного корня, . e >0; b > a.

2.Выполнить проверку применимости метода: если sgn f(a)×sgn f(b) > 0, то метод не применим; конец вычислений. Иначе выполнить 3.

3.Выполнить цикл пока b – a > e, т. е. длина отрезка изоляции корня больше заданной точности e.

3.1. Вычислить x = (a + b)/2; x – срединная точка интервала [a;b] есть приближение нуля f(x).