
- •Государственное образовательное учреждение высшего профессионального образования
- •Неопределенный интеграл
- •2 008
- •§ 1. Непосредственное интегрирование
- •Вариант 1.
- •§3. Интегрирование по частям
- •§4. Интегрирование функций, содержащих квадратный трёхчлен
- •§5. Интегрирование рациональных функций с помощью разложения на простейшие дроби. (Метод неопределённых коэффициентов)
- •§ 6 Интегрирования некоторых тригонометрических функций
- •§7. Интегрирование некоторых иррациональных функций
- •Вариант 1
§ 1. Непосредственное интегрирование
Этот метод применяется в тех случаях, когда используются непосредственно табличные интегралы: либо после алгебраических преобразований, либо после применения известных формул сокращенного умножения, либо при использовании тригонометрических преобразований подынтегрального выражения. Поэтому уместно привести некоторые из перечисленных преобразований:
Формулы сокращенного умножения
![]() ;
;
![]() ;
;
![]() .
.
Некоторые тригонометрические преобразования
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Действия со степенями
-
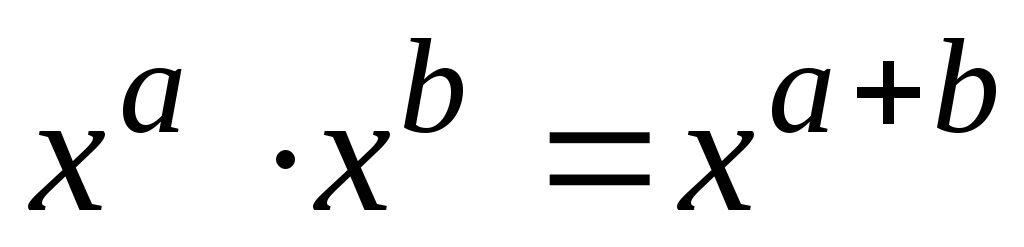 ;
;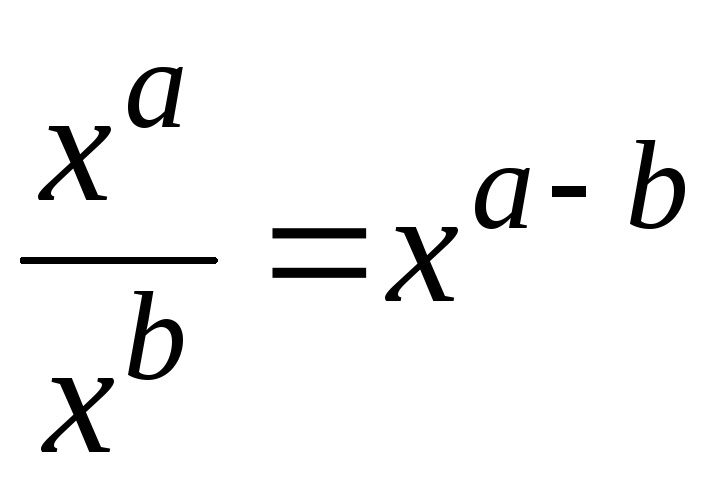 ;
;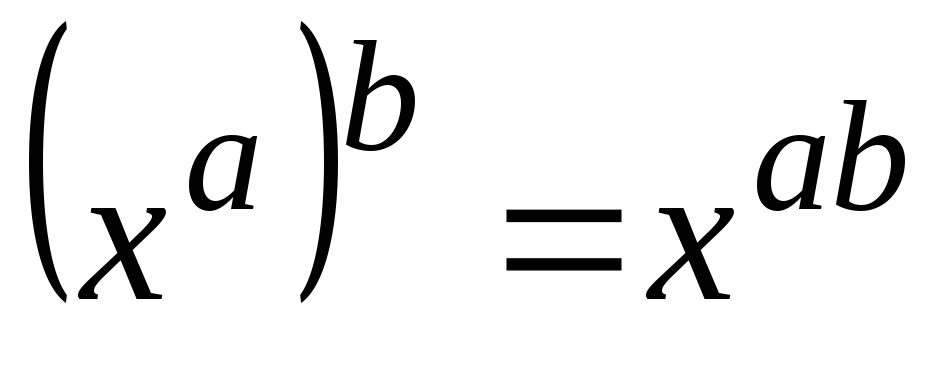 ;
;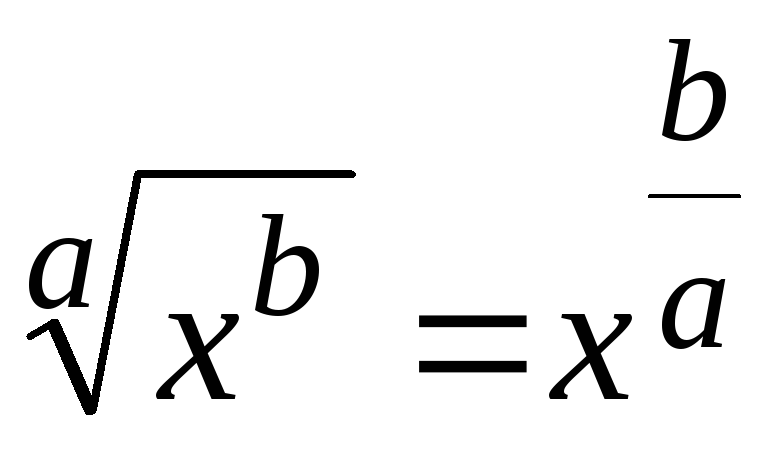 ;
;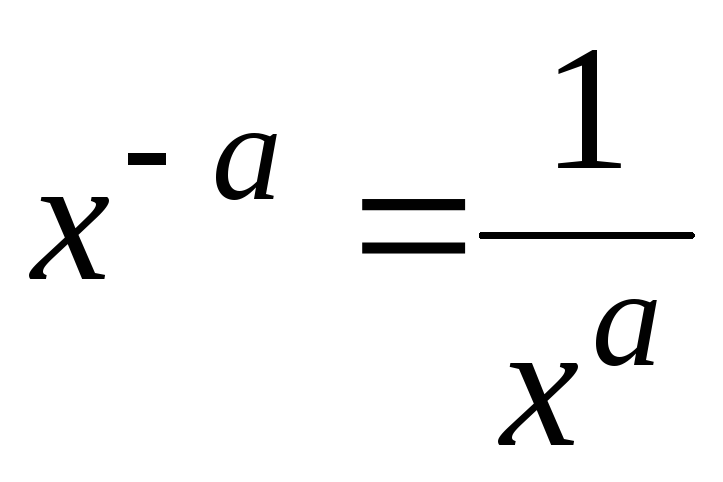 .
.
Пример.
Найти указанные интегралы. В первых двух задачах результаты проверить дифференцированием
Преобразуем подынтегральное выражение, т.е. сначала разделим числитель почленно на знаменатель, а затем применим свойство степеней:
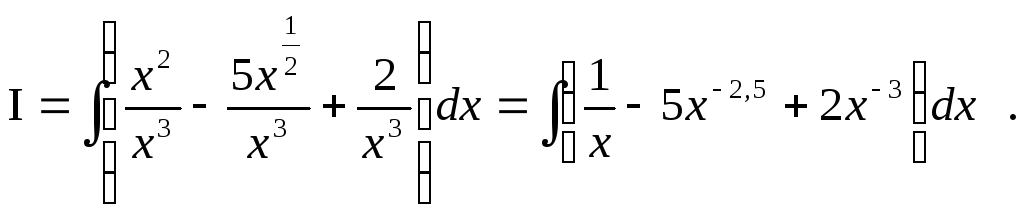
Теперь используя свойства неопределенного интеграла, получим
![]()
Это явно табличные интегралы, которые представлены формулами 2) и 3), следовательно
![]() ,
,
после несложных преобразований получим окончательно
![]() .
.
Проверим данный результат дифференцированием
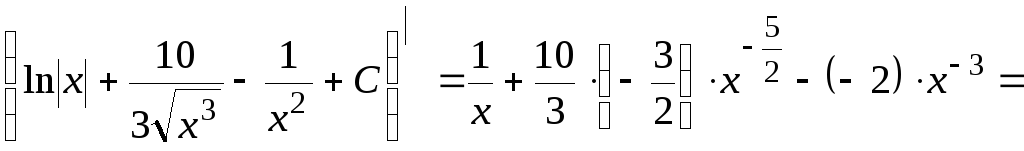
![]()
![]() ,
,
т.е. интегрирование проведено правильно.
Используя формулу возведения в квадрат, получим
![]() ,
,
опять используя свойства интеграла, запишем
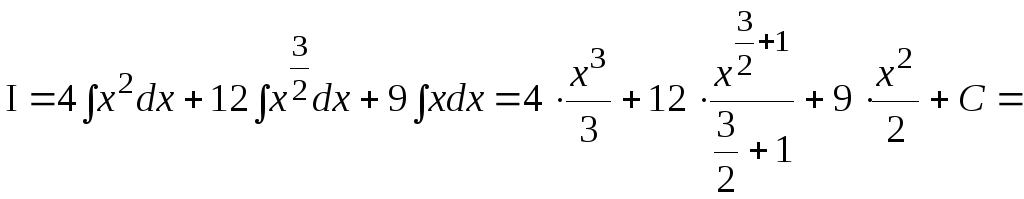
![]()
Проверим результат дифференцированием
![]()
![]()
![]() интегрирование проведено правильно.
интегрирование проведено правильно.
Перемножим многочлены
![]() .
.
Согласно свойствам неопределенного интеграла, получим
![]()
![]() .
.
![]() .
.
![]() .
.
![]()
![]()
 .
.
Задание 1
Найти неопределенные интегралы, применив непосредственное интегрирование. Результат первого интеграла проверить дифференцированием.
Вариант 1.
|
|
|
|
|
|
Вариант 2.
|
|
|
|
|
|
Вариант 3.
|
|
|
|
|
|
Вариант 4.
|
|
|
|
|
|
Вариант 5.
|
|
|
|
|
|
Вариант 6.
|
|
|
|
|
|
Вариант 7.
|
|
|
|
|
|
Вариант 8.
|
|
|
|
|
|
Вариант 9.
|
|
|
|
|
|
Вариант 10.
|
|
|
|
|
|
Вариант 11.
|
|
|
|
|
|
Вариант 12.
|
|
|
|
|
|
Вариант 13.
|
|
|
|
|
|
Вариант 14.
|
|
|
|
|
|
Вариант 15.
|
|
|
|
|
|
Вариант 16.
|
|
|
|
|
|
Вариант 17.
|
|
|
|
|
|
Вариант 18.
|
|
|
|
|
|
Вариант 19.
|
|
|
|
|
|
Вариант 20.
|
|
|
|
|
|
Вариант 21.
|
|
|
|
|
|
Вариант 22.
|
|
|
|
|
|
Вариант 23.
|
|
|
|
|
|
Вариант 24.
|
|
|
|
|
|
Вариант 25.
|
|
|
|
|
|
Вариант 26.
|
|
|
|
|
|
Вариант 27.
|
|
|
|
|
|
|
Вариант 28
|
|
|
|
|
|
|
Вариант 29
|
|
|
|
|
|
|
Вариант 30.
|
|
|
|
|
|
|
§ 2. Интегрирование заменой переменной (подстановкой)
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов
1)
![]() ,
где
,
где![]() - новая переменная.
- новая переменная.
Формула замены переменной при такой подстановке
![]() .
.
2)
![]() ,
где
,
где![]() - монотонная, непрерывно дифференцируемая
функция новой переменной
- монотонная, непрерывно дифференцируемая
функция новой переменной![]() .
Формула замены переменной в этом случае
имеет вид
.
Формула замены переменной в этом случае
имеет вид
![]() .
.
Согласно этим подстановкам интегралы приводятся к табличным.
Примеры.
Найти
![]() .
.
Решение:
примем за новую переменную
![]() тогда, согласно формуле
тогда, согласно формуле![]() получим
получим![]() ;
т.е.
;
т.е.![]() и интеграл примет вид
и интеграл примет вид![]() .
.
Вернем
к старой переменной,
![]() .
.
Найти:
![]()
Решение:
примем за новую переменную
![]() ;
тогда
;
тогда![]() .
.
Отсюда
![]() ;
;![]() ,
подставим в интеграл
,
подставим в интеграл
![]() .
.
Задание 2
Найти интегралы с помощью замены переменной.
Вариант 1
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 2
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 3
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 4
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 5
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 6
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 7
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 8
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 9
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 10
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 11
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 12
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 13
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 14
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 15
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 16
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 17
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 18
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 19
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 20
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)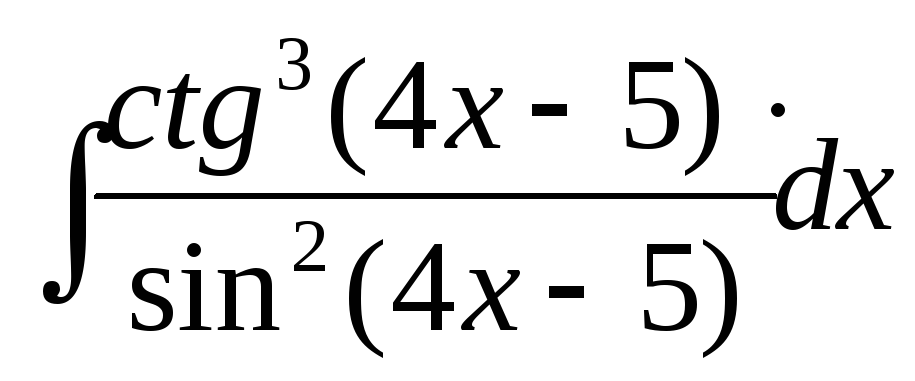
5)
![]() 10)
10)![]()
11)
![]()
Вариант 21
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 22
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 23
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 24
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 25
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 26
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 27
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 28
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 29
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
Вариант 30
1)
![]() 6)
6)![]()
2)
![]() 7)
7)![]()
3)
![]() 8)
8)![]()
![]()
4)
![]() 9)
9)![]()
5)
![]() 10)
10)![]()
11)
![]()
