
- •Государственное образовательное учреждение высшего профессионального образования
- •Неопределенный интеграл
- •2 008
- •§ 1. Непосредственное интегрирование
- •Вариант 1.
- •§3. Интегрирование по частям
- •§4. Интегрирование функций, содержащих квадратный трёхчлен
- •§5. Интегрирование рациональных функций с помощью разложения на простейшие дроби. (Метод неопределённых коэффициентов)
- •§ 6 Интегрирования некоторых тригонометрических функций
- •§7. Интегрирование некоторых иррациональных функций
- •Вариант 1
§4. Интегрирование функций, содержащих квадратный трёхчлен
Рассмотрим
интегралы ![]() или
или ![]() .
В знаменателе находится квадратный
трёхчлен, с отрицательным дискриминантом,
который не имеет корней и на множителе
не раскладывается.
.
В знаменателе находится квадратный
трёхчлен, с отрицательным дискриминантом,
который не имеет корней и на множителе
не раскладывается.
Такие
интегралы с помощью выделения полного
квадрата приводятся к табличным интеграла
вида: ![]() ,
,
![]() ,
,
![]() .
.
Пример.
Найти
интеграл ![]() .
.
Решение: Найдём дискриминант знаменателя
![]()
D=9-4*2*4=-23<0 – следовательно действительных корней нет.
Вынесем 2 за знак интеграла, получим
![]() .
.
Выделим полный квадрат
![]() -
-![]() +
+![]() =
=![]()
![]()
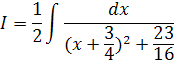
Это
табличный интеграл вида ![]() =
=![]() ∙arctg
∙arctg
![]() + c
+ c
u
=
x
+ ![]() ;
du=dx
;
du=dx
![]()
И согласно формуле (16)
I
=![]() (
(![]() ∙ arctg
∙ arctg
![]() )+С.
)+С.
Ответ:
![]() arctg
arctg![]() + С.
+ С.
Теперь
рассмотрим интегралы вида ![]()
В числителе появился многочлен первой степени, который не является производной знаменателя, а знаменатель по прежнему имеет отрицательный дискриминант.
Вычисление интегралов такого вида рассмотрим на примере.
Пример.
Найти
интеграл ![]() dx
dx
![]() Примем весь квадратный трёхчлен за
новую переменную
Примем весь квадратный трёхчлен за
новую переменную
![]() .
Найдём du=(4x+3)dx.
.
Найдём du=(4x+3)dx.
![]() ,
необходимо, чтобы du=(4x+3)dx.
Но в задании числитель (3x+5),
выделим из (3x+5)→
(4x+3)
следующим образом
,
необходимо, чтобы du=(4x+3)dx.
Но в задании числитель (3x+5),
выделим из (3x+5)→
(4x+3)
следующим образом
(3x+5)=![]() (4x+3)
-
(4x+3)
- ![]() +5=
+5=![]() (4x+3)
+
(4x+3)
+![]() , т.е. числитель получился состоящим из
суммы, которую распишем на два интеграла
, т.е. числитель получился состоящим из
суммы, которую распишем на два интеграла
I
=![]() dx+
dx+![]() =
=![]() +
+ 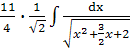
![]()
![]()
Тогда
I
=![]() +
+ ![]()
![]() +c.
+c.
Задание 4
Найти интегралы.
|
Вариант 1
|
Вариант 2 |
|
Вариант 3 |
Вариант 4 |
|
Вариант 5
|
Вариант 6 |
|
Вариант 7
|
Вариант 8 |
|
Вариант 9
|
Вариант 10 |
|
Вариант 11
|
Вариант 12 |
|
Вариант 13
|
Вариант 14 |
|
Вариант 15 |
Вариант 16 |
|
Вариант 17
|
Вариант 18 |
|
Вариант 19
|
Вариант 20 |
|
Вариант 21
|
Вариант 22 |
|
Вариант 23
|
Вариант 24 |
|
Вариант 25
|
Вариант 26 |
|
Вариант 27
|
Вариант 28 |
|
Вариант 29
|
Вариант 30 |
§5. Интегрирование рациональных функций с помощью разложения на простейшие дроби. (Метод неопределённых коэффициентов)
Перед
интегрированием рациональной дроби
![]() нужно
сделать следующее алгебраические
преобразования:
нужно
сделать следующее алгебраические
преобразования:
Если дана неправильная рациональная дробь, то выделить из неё целую часть, т.е.представить в виде:
![]() ,
где М(x)
– многочлен, а
,
где М(x)
– многочлен, а ![]() – правильная рациональная дробь.
– правильная рациональная дробь.
Разложить знаменатель дроби на линейные и квадратичные множители (если это возможно).
3) Правильную рациональную дробь разложить на простейшие дроби с неизвестными коэффициентами А, В, С,… это разложение записывается в зависимости от знаменателя дроби (если знаменатель дроби имеет различные линейные множители):
а)
![]() =
=![]() …;
…;
б)![]() ;
;
в)![]() ;
;
г)![]() .
.
4) Вычислить неопределённые коэффициенты А, В, С,… (Вычисление рассмотрим на конкретных примерах).
В результате интегрирование рациональной дроби сведётся к нахождению интегралов от многочлена и от простейших рациональных дробей.
Пример.
Найти интеграл
![]() .
.
Решение: Рассмотрим подынтегральную функцию.
Так как степень числителя больше степени знаменателя, т.е. дробь неправильная, то выделим из неё целую часть.
![]()
![]()
−![]()
![]()
−
![]()
Итак
получим ![]() ;
;
2) Разложим знаменатель оставшейся правильной дроби на множители, для этого найдём корни; в данном случае воспользуемся методом подбора корней: Например х₁=1
![]() =1-7+6=0
=1-7+6=0
Значит х₁=1 является одним из корней, а (х-1) один из множителей знаменателя. Выполним деление и получим степень знаменателя
![]()
![]()
−
![]()
![]()
![]()
−
![]()
![]()
−
![]()
0
Оставшийся
квадратный трёхчлен имеет корни х₂=2;
и х₃=-3;
т.е. ![]() отсюда получим
отсюда получим
![]()
![]() .
.
![]() и различны (случай (а))
и различны (случай (а))
Представим
теперь дробь ![]() в виде суммы простейших дробей с
неопределёнными коэффициентами
в виде суммы простейших дробей с
неопределёнными коэффициентами
![]()
И рассмотрим один из способов нахождения неопределённых коэффициентов как раз удобный для случая, когда знаменатель имеет неповторяющиеся множители первой степени.
Итак приведём правую часть к общему знаменателю
![]()
Т.к. знаменатели левой и правой частей равны, то приравняем числители
![]()
Далее будем подставлять значения х в получившееся уравнение, желательно, чтобы это были значения, являющиеся действительными корнями знаменателя при х=1 (можно найти А)
15∙1+12∙1=
А(1![]() 2)∙(1+3)+В∙0+С∙0;
2)∙(1+3)+В∙0+С∙0;
27=А∙(![]() 1)
∙4
1)
∙4
![]() 4∙А=27
4∙А=27
![]() А=
А=![]()
При
х
=![]() 3
(можно найти С)
3
(можно найти С)
15∙9+12∙(![]() 3)=А∙0+В∙0+С∙(
3)=А∙0+В∙0+С∙(![]() 3
3![]() 1)
(
1)
(![]() 3
3![]() 2);
2);
135![]() 36=(
36=(![]() 4)∙(
4)∙(![]() 5)∙С
5)∙С
99=20С
С=![]()
При х=2 (найдём В)
15∙4+12∙2=
А∙0+В(2![]() 1)(2+3)+
С∙0
1)(2+3)+
С∙0
84= 5В∙1
В=![]() .
.
Подставим найденные коэффициенты и вычислим интеграл:
![]()
![]()
+![]()
Пример. Найти интеграл
![]()
Решение: Так как подынтегральная функция является правильной рациональной дробью, то целую часть выделять не будем.
Знаменатель
дроби на множители больше не раскладывается,
т.к. квадратный трёхчлен ![]() - не имеет действительных корней (случай
(в)). Приступаем к разложению подынтегральной
дроби на сумму простейших дробей с
неопределёнными коэффициентами:
- не имеет действительных корней (случай
(в)). Приступаем к разложению подынтегральной
дроби на сумму простейших дробей с
неопределёнными коэффициентами:
![]()
В этот раз применим другой способ нахождения неопределённых коэффициентов. Также приведём правую часть к общему знаменателю
![]()
Т.к. знаменатели равны, то приравняем числители
![]()
Раскроем скобки, получим
![]() .
.
Теперь
сгруппируем в правой части члены с
одинаковыми степенями ![]() и вынесем их за скобки,
и вынесем их за скобки, ![]() .
.
Будем приравнивать коэффициенты левой и правой частей при одинаковых степенях х, т.е. получим систему
![]() А+В=1,
А+В=1,
![]() 4А+2В+С=
4А+2В+С=![]() 3,
3,![]()
![]() 5А+2С=2.
5А+2С=2.
из
первого уравнения В=1![]() А;
А;
из
третьего С=![]() ;
;
подставим
во второе уравнение 4А+2![]() 2А+
2А+![]() найдём А
найдём А
2А+![]()
4А+2-5А=![]() 10
10
![]() А=
А=![]() 12
12
![]() А=12.
А=12.
Тогда
В=1![]() 12=
12=![]() 11
11
![]() В=
В=![]() 11,
11,
С
=![]() ,
,
С=![]() 29.
29.
Подставим в подынтегральное выражение и вычислим интегралы
![]() +
+![]() dx
= 12 ln
dx
= 12 ln ![]() -
- ![]() dx.
dx.
Найдём второй интеграл
u=![]() ;
;
du=(2x![]() 4)dx;
4)dx;
11x+29=![]() ;
;
![]() dx=
dx=![]()
=![]()
Окончательно
I
= 12 ln
![]()
Пример.
Найти
интеграл ![]() dx.
dx.
Решение: Дробь правильная, значит целую часть выделять не будем.
Разложим знаменатель на множители,
![]()
Значит подынтегральное выражение примет вид:
![]() (случай (б)). Представим дробь в виде
суммы простейших дробей с неопределёнными
коэффициентами
(случай (б)). Представим дробь в виде
суммы простейших дробей с неопределёнными
коэффициентами
![]() .
.
Здесь можно применить комбинированный способ. Сначала найдём А при х=2
x![]() 5=
5=![]() ;
;
2![]() 5=
A
5=
A![]() ;
;
![]() ;
А
=
;
А
=![]() .
.
При
х=![]() 2
получим
2
получим
![]() ;
;
![]() 7=
7=
![]() 4∙C;
C
=
4∙C;
C
=![]()
Зная А и С будем определять В следующим образом:
х![]() 5=
5=![]() ,
,
подставим х=0
![]() 5=
5=![]() ,
,
![]() 5=
5=![]()
4В=![]()
4В=![]()
![]() В =
В =![]()
Найдём интеграл:
![]() dx
=
dx
=![]() +
+![]() +
+
+![]() .
.
Задание 5
Найти интегралы.
|
Вариант 1 |
Вариант 2
|
|
Вариант 3 |
Вариант 4
|
|
Вариант 5 |
Вариант 6
|
|
Вариант 7 |
Вариант 8
|
|
Вариант 9 |
Вариант 10 |
|
Вариант 11 |
Вариант 12
|
|
Вариант 13 |
Вариант 14
|
|
Вариант 15 |
Вариант 16 |
|
Вариант 17 |
Вариант 18
|
|
Вариант 19 |
Вариант 20
|
|
Вариант 21 |
Вариант 22 |
|
Вариант 23
|
Вариант 24
|
|
Вариант 25
|
Вариант 26
|
|
Вариант 27
|
Вариант 28
|
|
Вариант 29
|
Вариант 30
|
