§7. Интегрирование некоторых иррациональных функций

Рассмотрим следующие интегралы:

а)dx; б);

в)

С помощью определённых подстановок такие интегралы часто удаётся свести к интегралам от рациональных функций или тригонометрических, которые значительно проще вычисляются.

а) Интегралы вида dx,

где - рациональная функция;

целые числа. С помощью подстановки , где S – наименьшее общее кратное чисел указанный интеграл преобразуется в интеграл от рациональной функции.

Пример. Найти интеграл

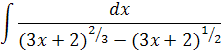
Решение: Здесь n₁=3; n₂=2; значит S=6; применим подстановку , тогда x=и, следовательно,

I==

- t-1

1

=2

Возвращаемся к старой переменной.

Т.к. ,то

I=

б) Интеграл вида .

С помощью подстановки . Этот интеграл приводится к интегралу

, рассмотренному выше в…§4

Пример. Найти интеграл I=

Решение: Применим подстановку x-1=; тогда x=

Получим интеграл

I=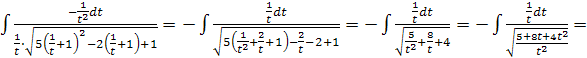

Вернёмся к старой переменной.

Т.к. x1 =; то t= получим

I=

в) Интеграл от дифференциальных биномов где m, n, p- рациональные числа.

Как доказал П. Л. Чебышев, такой интеграл выражается через элементарные функции только в трёх случаях:

1. p - целое число, тогда данный сводится к интегралу от рациональной функции с помощью подстановки x= 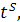где 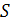– наименьшее общее кратное знаменателей дробей m и n.

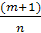2. - целое число, в этом случае данный интеграл рационализируется с помощью подстановки ,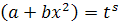

где – знаменатель дроби p .

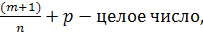3. в этом случае к той же цели ведёт подстановка , где – знаменатель дроби p.

Пример.

1. Найти интеграл:

Решение: Запишем подынтегральную функцию в виде , т.е. p=-8 – целое число. Значит следует применять подстановку x=, тогда dx=4dt и искомый интеграл принимает вид:

I=

=4∙

Вернёмся к старой переменной, т.к. x=, то t= и следовательно

I=

2. Найти интеграл

I=

Решение: Запишем подынтегральную функцию в виде:

т.е. m=3; n=2; p= так как =целое число, то применим подстановку , отсюда -2x dx=2t dt; x dx=-t dt;

Следовательно

Вернёмся к старой переменной, т.к. , то получим:

I=

3. Найти интеграл

Решение: Запишем подынтегральную функцию в виде:

Здесь m=-4; n=2; p= а – целое число.

Поэтому применим подстановку

тогда -2

Преобразуем интеграл:

I=

Следовательно:

I=-

4. Найти интеграл

I=

Решение: Примем

тогда: I=

=

=

Задание 7

Подобрать подстановку и найти интегралы:

Вариант 1

1)

2)

3)

4)

5) а)

Вариант 2

1)

2)

3)

4)

5) а)

Вариант 3

1)

2)

3)

4)

5) а)

Вариант 4

1)

2)

3)

4)

5) а)

Вариант 5

1)

2)

3)

4)

5) а)

Вариант 6

1)

2)

3)

4)

5) а)

Вариант 7

1)

2)

3)

4)

5) а)

Вариант 8

1)

2)

3)

4)

5) а)

Вариант 9

1)

2)

3)

4)

5) а)

Вариант 10

1)

2)

3)

4)

5) а)

Вариант 11

1)

2)

3)

4)

5) а)

Вариант 12

1)

2)

3)

4)

5) а)

Вариант 13

1)

2)

3)

4)

5) а)

Вариант 14

1)

2)

3)

4)

5) а)

Вариант 15

1)

2)

3)

4)

5) а)

Вариант 16

1)

2)

3)

4)

5) а)

Вариант 17

1)

2)

3)

4)

5) а)

Вариант 18

1)

2)

3)

4)

5) а)

Вариант 19

1)

2)

3)

4)

5) а)

Вариант 20

1)

2)

3)

4)

5) а)

Вариант 21

1)

2)

3)

4)

5) а)

Вариант 22

1)

2)

3)

4)

5) а)

Вариант 23

1)

2)

3)

4)

5) а)

Вариант 24

1)

2)

3)

4)

5) а)

Вариант 25

1)

2)

3)

4)

5) а)

Вариант 26

1)

2)

3)

4)

5) а)

Вариант 27

1)

2)

3)

4)

5) а)

Вариант 28

1)

2)

3)

4)

5) а)

Вариант 29

1)

2)

3)

4)

5) а)

Вариант 30

1)

2)

3)

4)

5) а)

83