metod07

Вычислительная математика Практическая работа 7

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Составитель С.Ю. Кириллова

ЗАДАНИЕ НА РАБОТУ:

1) изучить примеры 7.1-7.5;

3) решить в средеMathCAD (или составить программу решения на любом языке про- граммирования) задачи 7.1 – 7.5.

ПРИМЕРЫ

Пример 7.1. Локализация корней.

Пример 7.2. Решение уравнения методом бисекции. Пример 7.3. Решение уравнения методом Ньютона.

Пример 7.4. Чувствительность метода Ньютона к выбору начального приближения. Пример 7.5. Приведение уравнения к виду, удобному для итераций.

Решение примеров в среде пакета MathCAD: файлы R7_ex1.mcd – R7_ex5.mcd.

ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ

Метод простой итерации (последовательных приближений)

Для применения метода простой итерации следует исходное уравнение f (x) = 0

преобразовать к виду, удобному для итерацииx = ϕ(x). Это преобразование можно выпол-

нить различными способами. Функцияϕ(x) называется итерационной функцией. Расчетная

формула метода простой итерации имеет вид:

x(n+1)= ϕ(x(n)).

Теорема о сходимости метода простой итерации. Пусть в некоторой δ- окрестности корня x функция ϕ(x) дифференцируема и удовлетворяет неравенству ϕ′(x) ≤ q , где 0 ≤ q <1 – постоянная. Тогда независимо от выбора начального приближения из указанной

δ–окрестностиитерационная последовательность не выходит из этой окрестности, метод

сходится со скоростью геометрической последовательности и справедлива оценка погрешности:

x(n)− x ≤ 1−qq x(n)− x(n−1).

Критерий окончания итерационного процесса. При заданной точности ε > 0 вычис-

ления следует вести до тех пор пока не окажется выполненным неравенство

	x(n)− x(n−1)		<	1−q		δ. Если величина0 < q ≤ 0.5 , то можно использовать более простой
					q
								x(n)− x(n−1)		< ε.
критерий окончания итераций:

Ключевой момент в применении метода простой итерации состоит в эквивалентном преобразовании уравнения. Способ, при котором выполнено условие сходимости метода простой итерации, состоит в следующем: исходное уравнение приводится к виду

x = x − αf (x) , гдеα – итерационный параметр. Предположим дополнительно, что произ- воднаяf ′ знакопостоянна иm ≤ f ′(x) ≤ M на отрезке[a,b]. Тогда при выборе итераци-

онного параметра α =	2	метод сходится и q =		M − m		< 1.
	m + M			M + m

Метод последовательных приближений обладает локальной сходимостью со скоро- стьюпервого порядка (линейной), то есть областью его сходимости является малая окрест- ность корняx . Достоинство метода заключается в том, что не накапливаются ошибки вы- числений. Ошибка вычислений эквивалентна ухудшению очередного приближения, что мо- жет отразиться только на числе итераций, но не на точности результата. Метод устойчив да- же по отношению к грубым ошибкам.

Метод Ньютона (касательных)

Одним из популярнейших итерационных методов решения нелинейных уравнений, что связано с его идейной простотой и быстрой сходимостью, являетсяметод Ньютона (в зарубежной литературе– метод Ньютона-Рафсона). Расчетная формула метода Ньютона имеет вид:

x(n+1)= x(n)− f (x(n) ).

f ′(x(n) )

Геометрически метод Ньютона означает, что следующее приближение к корню есть точка пересечения с осьюОx касательной, проведенной к графику функцииy =

x(n+1)

f (x)

в точке (x(n) , f (x(n) )).

Теорема о сходимости метода Ньютона. Пусть x – простой корень уравнения f (x) = 0 , в некоторой окрестности которого функция дважды непрерывно дифференцируе-

ма. Тогда найдется такая малаяδ - окрестность корняx , что при произвольном выборе на-

чального приближения x(0) из этой окрестности итерационная последовательность метода

Ньютона не выходит за пределы окрестности и справедлива оценка

x(n+1)− x		≤	1			x(n+1)− x		2 .
			δ

Критерий окончания итерационного процесса. При заданной точности ε > 0 вычис-

ления следует вести до тех пор, пока не окажется выполненным неравенство

x(n)− x(n−1)< ε .

Упрощенный метод Ньютона: x	= x −	f (xn )	, n=0,1,…
n+1	n	f ′(x0 )

Метод Ньютона обладает высокой скоростью сходимости – второго порядка (квадратичной), но сходимость являетсялокальной. Неудачный выбор начального приближения может дать расходящуюся итерационную последовательность. Поэтому методу Ньютона часто предшествуеткакой-либонадежно сходящийся алгоритм(например, метод половинно- го деления), а метод Ньютона используют на завершающей стадии решения уравнения.

Модификации метода Ньютона. Метод секущих

Трудностью метода Ньютона является необходимость вычисления производной на каждом итерационном шаге. Далеко не всегда бывает удобно находить аналитическое выра- жение для производной функции. Однако, в этом и нет особой необходимости: поскольку на каждом шаге мы получаемприближенное значение корня, можно для его вычисления ис- пользоватьприближенное значение производной:

	′	f (x +x) −f (x)		f (x +x) −f (x)
	f (x) = lim		≈		.
		x		x
	x→0

В качестве малой величины x можно взять, например, заданную точность вычисленийε ,

тогда расчетная формула примет вид

	xk+1	= xk −	f (xk )ε
			f (xk + ε ) −f (xk ),		(7.1)

что составляет основу разностного метода Ньютона.

С другой стороны, для вычисления производной можно воспользоваться значениями функции, полученными на двух предыдущих шагах,

	xk+1 = xk−	f (xk )(xk−1 −xk )	,	(7.2)
		f (xk−1) −f (xk )

где k = 1,2,3,..., аx0 иx1 должны задаваться. В таком виде метод называетсяметодом секущих (secant method). При этом, однако, возникает проблема с вычислением первого

приближения. Обычно полагают, чтоx1 = x0 + ε , то есть первый шаг вычислений прово-

дится с использованием формулы (7.1), а все последующие– с использованием формулы

(7.2).

Формула (7.2) определяет новый метод какдвухшаговый. Его геометрическая интер- претация: xk +1 есть абсцисса точки пересечения с осьюOx прямой, проведенной через точ-

ки (xk−1; f (xk−1)) и(xk ; f (xk )), т.е. секущей.

Используя метод секущих, мы не можем гарантировать, что корень находится между двумя последними приближениями. Метод секущих и метод хорд определяются однотипны- ми формулами, но порождающие их идеологии различны, что сказывается на свойствах и скорости сходимости генерируемой ими последовательности приближений. Метод секущих обладает квадратичной сходимостью.

Высокий порядок скорости сходимости метода секущих в сочетании с минимальными вычислительными затратами – одно вычисление функции на один итерационный шаг– вы- водит этот метод на первое место по эффективности решения скалярных нелинейных урав- нений среди прочих итерационных методов. Именно эта вычислительная схема реализована во встроенной функцииroot пакетаMathcad.

ПОИСК КОРНЕЙ УРАВНЕНИЙ В MATHCAD

Найдем нули функции f( x)			cos( x)						на интервале x=[–2,7], используяMathcad.
			( x				5)2

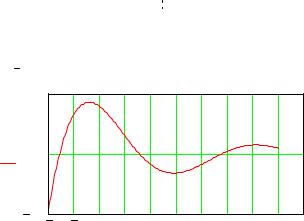
Изобразим сначала функцию на графике.

x 2,

f( x)

1.95.. 7
0.05
0
0.05	2	1	0	1	2	3	4	5	6	7	8
						x

На заданном интервале функция три раза обращается в ноль. Определим нули функ- ции, используя встроенную функциюroot(f(x),x). Первый аргумент– функция, нуль которой необходимо найти, второй– переменная, которую необходимо варьировать. (Вообще говоря,

r( x)

root( f( x) , x)

функция f может быть функцией многих переменных и необходимо указывать, по какой именно переменной мы ищем нуль функции.) Кроме того, необходимо задать начальное приближение поиска. Точность вычислений(условие прекращения итераций численным ал- горитмом) задается встроенной переменнойTOL. По умолчанию ее значение равно0,001. Это значение можно изменить либо через менюMath/Built–In Variables или непосредствен-

но в тексте документа: TOL 10 9

Задаем начальное приближение: x 1

И вычисляем корень: root( f( x) , x) = 1.570796327

Если требуется найти несколько корней, как в нашей задаче, то имеет смысл опреде-

лить новую функцию:

Функция r(x) возвращает значение корня ближайшее кx1, то есть начальное прибли- жение мы задаем через аргумент функции. Задаем вектор начальных приближенийx и нахо- дим соответствующие им корниX:

xi

i		0.. 2		X		r x	Xi
			1	i		i	1.570796327
			1
							1.570796327
			4
							4.712388981

Для данного примера корни легко могут быть найдены аналитически. Они равны на заданном интервале −π/2, π/2 и 3π/2. Полученный численный результат с заданной точно- стью совпадает с точным решением.

Определение новой функции целесообразно и в том случае, когда мы хотим исследо- вать зависимость решения от параметра. Пусть функция зависит от параметраa

z( a, x)		root		cos( a.x)					, x
				( x				5)2

Первый аргумент функции z задает значение параметра, второй– начальное прибли- жение. Найдем корни уравнения при значениях параметра1 и2.

z( 1, 1) = 1.571

z( 2, 1) = 0.785

Если мы хотим получить комплексный корень, то начальное приближение следует за-

давать комплексным:

z(i

, i ) =

7.459 10

9 +1.571i

Нахождение корней полиномов

Для нахождения

корней полиномов имеется встроенная

функция

polyroots(a).

Аргументом функции является вектор коэффициентов полинома

a + a x+ a x2

+ + a xn

,

0

1

2

n

то есть для уравнения 3x2 + 2x +1 = 0 вектор а имеет вид

i

0.. 2

ai

polyroots ( a) =

0.333

0.471i

1

0.333+ 0.471i

2

3

Если в полиноме отсутствуют некоторые степени, то на соответствующих местах сле- дует писать0. Пусть требуется найти корни полиномаp(x) = x3 + 2x2 −1

1 К сожалению, это не всегда так. Если начальное приближение выбрано неудачно и значение производной в этой точке близко к нулю, то, вообще говоря, найденный корень может быть не ближайшим к начальному приближению. В качестве примера решите самостоятельно

задачу поиска корня уравнения sin(x) = 0 , выбрав в качестве начального приближения число близкое кπ2 . Чем ближе кπ2 будет вы- бранное значение, тем более далекий от0 корень мы будем получать.

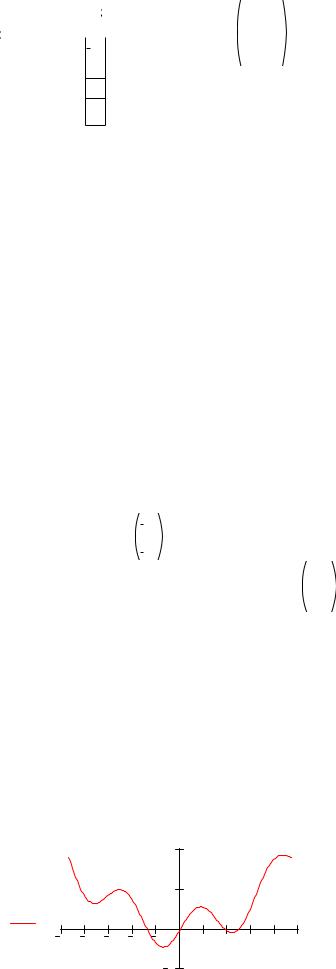
			ai					1.618
i		0.. 3				polyroots ( a ) =		1
			1
					0.618
			0

2

1

Коэффициенты полинома могут быть и комплексными.

Иногда исходный полином имеется не в развернутом виде, а, например, как произве- дение нескольких полиномов. В этом случае определить все его коэффициенты можно, вы- делив его и выбрав в менюSymbolics (Символика) пунктExpand (Разложить). В результа- те символьный процессорMathcad сам преобразует полином в нужную форму, пользовате- лю нужно будет корректно ввести аргументы функцииpolyroots.

Нахождение корней уравнений путем символических преобразований.

Во многих случаях Mathcad позволяет найти аналитическое решение уравнения. Для этого необходимо воспользоваться пунктомSolve for Variable из пункта менюSymbolics. Для того чтобы найти решение уравнения необходимо записать выражение и выделить в нем пе- ременную(поставить указатель курсора возле переменной). Это необходимо для того, чтобы показать, какая именно величина является переменной, а какая– фиксированным парамет- ром. После этого выбираем из пункта менюSymbolic подпунктSolve for Variable

cos(a.x)					1		.	π
					решение готово ––>
						2		a
(x				5)2

Обратите внимание! В данном случае был найден только один корень, хотя, оче- видно, их бесконечно много.

В случае полинома Mathcad, а точнее– встроенный символический процессорMa-

ple – находит все корни.									1
x2				2.x				1 –>		Для этого примера найдено 2 корня, хотя они и вырожде-
									1

ны. Пример с комплексными корнями: x2			1 ––>		i
					i .

Mathcad 2000 представляет ряд дополнительных возможностей для поиска корней уравнений. Функцияroot(f(var1, var2, ...),var1, [a, b]) имеет теперь два необязательных аргу- ментаa иb, которые определяют границы интервала, на котором следует искать корень. На концах интервала[a,b] функцияf должна менять знак(f(a)f(b)<0). Задавать начальное при- ближение для корня не нужно. В данном варианте функцияroot использует алгоритм Ридде- ра или Брента. Продемонстрируем использование расширенного варианта поиска корней на

примере функции

f(x) := 0.04× x2 + sin(x)

Для оценки местоположения корней построим график этой функции

x:=-3 ×p,-3 × p +0.1..3 × p
					4
					2
f(x)
10	8	6	4	2	0	2	4	6	8	10
					2
					x

root(f(x) , x, −1, 8) = 0

root(f(x), x, −10, −0.1) = −2.818

На интервале [1,8] функция имеет два корня. Mathcad 2000 смог найти только один из

них.

Дополнительные возможности появились и для нахождения корней полиномов. Функцияpolyroots может использовать два различных алгоритма поиска корней– метод Ла- герра(LaGuerre) и метод сопровождающей матрицы(Companion Matrix). Переключение ме- тодов осуществляется в контекстном меню, которое вызывается нажатием правой кнопки мыши, когда указатель установлен на имя функции. Для того, чтобы оставить заMathcad вы- бор метода решения, установите флажокAutoSelect (Автоматический выбор).

Решение систем уравнений

Системы линейных и нелинейных уравнений и неравенств позволяет решать на Mathcad блокGiven в сочетании с функциейFind.

Система уравнений и/или неравенств должна быть записана после или правее слова

Given.

При записи уравнений и/или неравенств следует пользоваться панелью инструментовBoolean (Булевы операторы) При вводе с клавиатуры вместо знака= следует набирать

Ctrl+=.

Перед словом Given необходимо указывать начальные приближения для всех пере- менных, т.к. данный вычислительный блок использует для поиска решения итерационные методы.

Блок Given не пригоден для поиска индексированных переменных.

Если мы хотим найти комплексный корень, следует задавать комплексное начальное приближение.

Признаком окончания системы служит функция Find, если мы хотим найти точное решение системы, либо функцияMinerr, если система не может быть решена точно, и мы хотим найти наилучшее приближение, обеспечивающее минимальную погрешность.

Аргументами функций Minerr иFind являются неизвестные, относительно которых решается система. ФункцииMinerr иFind должны иметь столько же или меньше аргумен- тов, сколько уравнений и неравенств содержит блокGiven. Если окажется, что блок содер- жит слишком мало уравнений или неравенств, то его можно дополнить тождествами или по- вторяющимися выражениями.

В том случае, если решение не может быть найдено при заданном выборе начального приближения, появится сообщение в красной рамкеDid not find solution – решение не най- дено.

Вычислительный блок использует константу CTOL в качестве погрешности выпол- нения уравнений, введенных после ключевого словаGiven. Например, еслиCTOL=0.001, то уравнениеx=10 будет считаться выполненным и приx=10.001, и приx=9.999. По умол- чанию значениеCTOL равно0,001. Это значение можно изменить либо через меню

Math/Built–In Variables или непосредственно в тексте документа: СTOL 10 9.

Функция Find реализует градиентные численные методы. Можно выбрать в контек- стном меню в категорииNonlinear, появляющемся после щелчка правой клавишей мыши на словеFind, один из трех методов: Conjugate Gradient (Сопряженных градиентов), QuasiNewton (Квази-Ньютоновский) илиLevenberg-Marquardt (Левеннберга-Маркардта).

Зададим начальные приближения и решим систему нелинейных уравнений.

x		1	y			1							Find(x, y ) = 5
given			x2				y		23	x2 . y		50
													2

Если необходимо найти решение при различных начальных приближениях, имеет

смысл определить новую функцию

given x2		y		23	x2.y		50	f( x, y )		Find( x, y )

Обратите внимание! В этом случае не нужно задавать начальные приближения пе- ред началом блокаGiven – Find. Начальные приближения задаются в качестве аргументов функцииf(x,y)

f( 1, 1) =	5		f(	1, 1) =				5
						2
	2
f( i , 1) =	1.414i						1.414i
			f(	i , 1) =
		25					25

Подобным же образом можно решать системы, зависящие от параметра.

given x2

y2

R2

y

x

g( x, y , R)

Find( x, y )

g( 1, 1, 1) =

0.707

g(

1,

1, 1) =

0.707

0.707

0.707

ЗАДАЧИ

Задача 7.1. Даны два уравнения f(x)=0 иg(x)=0. Найти с точностьюε =10−10 все корни уравнений, содержащиеся на отрезке[a, b]. Для решения задачи использовать метод бисекции. Найти корни с помощью встроенной функции root пакетаMATHCAD.

	ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:
1.	Найти аналитическое решение уравнения f(x)=0.
2.	Используя пакет MATHCAD, локализовать корниf(x)=0 графически.
3.	Используя программу bisec (см. пример 7.2), найти корни уравненияf(x)=0 с
точностью ε с помощью метода бисекции.
4. Используя		встроенную функции root пакета MATHCAD, найти корни уравнения
f(x)=0 с точностьюε .
5.	Аналогично п. 1-4 попытаться найти корни уравненияg(x)=0. Объяснить получен-
ные результаты.
Фрагмент решения задачи в среде пакета MathCAD: файл R7_z1.mcd.
Задача 7.2.		Найти указанный в варианте корень уравнения f(x)=0 с точностью

ε =10−6 , двумя способами.

а) Использовать метод бисекции. Предварительно определить отрезок локализации

[a, b].

b) Использовать метод Ньютона. В качестве начального приближения для метода Ньютона взять середину отрезка локализации из п. а).

Сравнить число итераций в п. a), b).

Задача 7.3. Локализовать корни уравнения f(x)=0 и найти их с точностьюε =10−5 , используя метод простой итерации. К видуx=ϕ(x), удобному для итераций, уравнениеf(x)=0

привести двумя способами.

x=x-αf(x),

где α=2/(M+m),

a)

Преобразовать

уравнение к

виду

0 < m ≤ f '(x) ≤ M , аx принадлежит отрезку

локализации [a, b].

b) Любым

другим

преобразованием уравнения. Проверить достаточное условие

сходимости метода.

Использовать

критерий

окончания

итерационного

процесса

вида

| x

(n)

− x

(n−1)

|<

1−q

ε , где в п. a)

q=(M-m)/(M+m),в п. b)q = max

′

.

q

ϕ (x)

x [a,b]

Сравнить число итераций и значения величины q в п. a), b).

Задача 7.4. Локализовать корни уравнения f(x)=0. Найти их с точностьюε =10−8 , используя методы простой итерации и Ньютона. Сравнить скорость сходимости методов(по числу итераций). Найти корни, используя встроенную функциюpolyroots.

Задача 7.5. Локализовать корни уравнения f(x)=0. Найти их с точностьюε =10−5 и

ε =10−12 , используя метод Ньютона, упрощенный метод Ньютона и метод секущих. Срав- нить скорость сходимости методов(по числу итераций) для каждого значенияε .

Задача 7.6. Найти с точностью ε =10−6 все корни системы нелинейных уравнений

f1(x1,x2 )= 0,

f2 (x1,x2)= 0,

используя метод Ньютона для системы нелинейных уравнений. Найти корни с помощью встроенного блока решения уравнений Given Find пакетаMATHCAD.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1.Используя пакет MATHCAD, локализовать корни системы уравнений графически.

2.Составить программу-функцию, вычисляющую корень системы двух нелинейных

уравнений по методу Ньютона с точностью ε. Предусмотреть подсчет количества итераций.

Для решения соответствующей системы линейных алгебраических уравнений использовать встроенную функцию lsolve пакета MATHCAD.

3.Используя составленную программу, вычислить все корни заданной системы с точ- ностью ε.

4.Используя встроенный блок Given Find пакета MATHCAD, найти все корни сис-

темы с точностью ε. Сравнить с результатами, полученными в п. 3.

УКАЗАНИЕ. В п. 1 привеcти уравнения системы к видуx2 = gi (x1) (либоx1 = gi (x2 ) ), i=1, 2, можно с помощью пункта меню Symbolic пакетаMATHCAD следую- щим образом:

1)набрать уравнение (знак равенства набирается с помощью комбинации клавиш

[CTRL] и[=]);

2)выделить переменную, относительно которой нужно разрешить уравнение, щелк- нув на ней мышью;

3)Выполнить команду Symbolic / Solve for Variable.

Фрагмент решения задачи в среде пакета MathCAD: файл R7_z1.mcd.

Варианты заданий даны в ПРИЛОЖЕНИИ 7.A.

Вариант выбирается в соответствии с номером студента в журнале группы, при необходимости по модулю количества вариантов в таблице.

ПРИЛОЖЕНИЕ 7.A.

Таблица к задаче 7.1

N						f(x)													g(x)								[a, b]
1.	(sinx)			2		5				1						(sinx)			2			1					[0,1]
					− 6 sinx +					6										− sinx +		4
2.	(sinx)		2			7				1						(sinx)		2			2		1				[−1,0]
				+					sin x +										+		3 sinx +		9
							12				12
3.	(sinx)	2				1				1						(sinx)	2				2		1				[−0.5,0.5]
				−				sin x −											−		5 sinx +
						30				30													25
4.	(cosx)	2				2				1						(cosx)	2				2		1				[0,2]
				+				cos x −											−		7 cosx +
						35						35												49

5.	(cosx)	2				æ				1													1					ö																			1					(cosx)	2				-				2			cos x +									1					[0,1.5]
			-			ç										+													÷cosx +																																												2
																							4																																							2
						è					2																	ø							4												2
6.	(cosx)								2											1															1																	(cosx)		2							1										1							[0,2]
											+									2 cosx +																																						+			3 cosx					+
																																	18																																						36
7.		(lnx)									2			- 5lnx + 6																																						(lnx)				2			- 4lnx + 4																			[5,25]
8.			(lnx)										2						- ln x -2																																	(lnx)					2		+ 2lnx +1																			[0.1,10]
9.		(lnx)2 -																				3 lnx +										1																				(lnx)2 - lnx +														1												[0.1,2]
																				4												8																																		4
10.	(tgx)				2																																															(tgx)					2																					[-1.2,1]
						+ ( 3-1)tgx -																													3																								- 2tgx+1
11.		(tgx)							2		-									28							tgx +					1																				(tgx)				2			- 6tgx +9																			[0,1.5]
																				9												3
12.									2							53																3																						2					1									1									[	-
		(tgx)										- 6 tgx -2																																								(tgx)						- 3tgx+																				0.5,1.5]
																																																																			36
13.						x4- 7x2+10																																														x4- 4x2+ 4																										[0,3]
14.					x		4			-				10									x				2				+1																					x4- 6x2+ 9																										[0,2]
																3
15.					x		4		-					13									x				2			+ 3																						x		4				- x				2	+		1													[0,3]
																2																																																	4
16.																				5													1																												2										1							[ 1,0]
	(sinx)									2																																										(sinx)			2																							-
														+								6 sinx +											6																										+		3 sinx +										9
17.	(sinx)							2												7															1																	(sinx)		2							1										1							[0,1]
															-											sin x +																																-			2 sinx					+
																			12															12																																				16
18.								2												1															1																			2							1										1						[	-
	(sinx)														+											sin x -																										(sin x)						+ 3sinx +																				0.5,0.5]
																	30																	30																																			36
19.	(cosx)							2								2																			1																	(cos x)		2							2										1							[0,3]
											-															cos x -																																- 5 cosx								+
																	35																		35																																				25
20.	(cosx)	2				æ				1													1					ö																			1					(cosx)		2				-			1	cos x				+					1							[0,2]
				+ ç														-											÷cosx -
																							4																																						2										16
						è					2																	ø							4												2
21.	(cosx)2 -																			1 cos x +															1																	(cos x)2 -									2 cosx +										1							[0,2]
																																	18																																						9
																				2																																									3
22.		(lgx)2 +																				5 lg x -										2																				(lgx)2 -									2 lg x +							1										[0.001,3]
																				3												3																													3							9
23.			(lg x)2 - lgx - 3																																																	(lgx)2 - 3lgx +																9										[0.1,35]
																															4																																					4
24.		(lgx)								2										3												1																				(lgx)					2		+ 2lg x +1																			[0.01,3]
														+								4 lg x -										4
25.	(tgx)			2		- (1+																	1						)tgx			+			1																	(tgx)					2		- 2tgx+1																			[0,1]
																										3													3

26.			(tgx)2 -									7 tgx-					1				(tgx)2 +					1 tgx+						1			[-0.5,1.5]
																	2														16
												4														2
27.			(tgx)					2		+		37		tgx +1							(tgx)2 +12tgx+ 36														[-1.5,0]
												6
28.					x4-11x2+ 24																	x4- 6x2+ 9													[1,3]
29.					x	4		-		26			x	2	+1							x4-10x2+ 25													[0,3]
										5
30.					x	4		-		21			x	2	+ 5								x	4	- x		2		+	1					[0,5]
										2																				4
			Таблица										к задаче 7.2												Таблица к задаче 7.3
N			f(x)														Найти корень							N										f(x)
1.	e−x -2 +x2															отрицательный						1.							sin x + 2x2 + 4x
2.	xex - x-1															положительный						2.							e−x - lg(1- x2)- 2
3.																положительный						3.							sin(x + 2)- x2 + 2x -1
	ex +1-9 -x2
4.	(x +1)× e			x+1			- x -						2			наибольший по						4.							(x −1)sh(x +1) −x
																модулю
5.			- cosx													все корни						5.							x - e−x2
		x
																Таблица			к задаче 7.4
					f(x) º P(x) = x5 + a x4														+ a x3 + a x2							+ a x+ a
												5					4		3			2							1		0
N			a4											a3					a2										a1						a0
1.	4.545004									-3.055105								-18.06895					4.002429											4.722482
2.	-2.656764									-3.406111								10.89372					-1.752935											-3.423612
3.	-4.556062									2.93309								9.274868					-10.32081											0.422098
4.	7.809249									16.28542								-2.771356					-27.95304											-11.33921
5.	-13.0072									60.24546								-122.0716					105.6798											-30.19201

Таблица

к задаче 7.5

N

f(x)

N

f(x)

1.

ex- 3

6.

xln x- x2 + 3x-1

x

2.

7.

x3 - 0.9x 2 -x - 0.1

2 -x2 -ex

3.

ln x − 2cosx

8.

e

−x

- 5x

2

+10x

4.

9.

ln(2x - x2 )+ 2-

xecosx -1

x

5.

e−(x+1)+ x2+ 2x -1

10.

+ x2 -10

x