3126 Моделирование контрольная

3126	МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
	ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»

Кафедра «Автоматика, телемеханика и связь на железнодорожном транспорте»

РЕШЕНИЕ МАТЕМАТИЧЕСКИХ И ПРИКЛАДНЫХ ЗАДАЧ СРЕДСТВАМИ MATHCAD И DELPHI

Методические указания к выполнению контрольных работ по дисциплине «Математическое моделирование систем и процессов»

для студентов специальности 190901 «Системы обеспечения движения поездов» очной и заочной форм обучения

Составители: Ф.Р. Ахмадуллин В.Г. Волик В.Б. Гуменников

Самара

2012

1

УДК 656.254.16

Решение математических и прикладных задач средствами Mathcad и Delphi :

методические указания к выполнению контрольных работ по дисциплине «Математическое моделирование процессов и систем» специальности 190901 «Системы обеспечения движения поездов» для студентов очной и заочной форм обучения / составители : Ф.Р. Ахмадуллин, В.Г. Волик, В.Б. Гуменников. – Самара : СамГУПС, 2012. – 36 с.

В методических указаниях приводится решение задачи формирования гармонических сигналов методами цифрового синтеза, задачи моделирования рельсовых цепей, а также рассматриваются вопросы алгоритмизации сложных информационнологических задач, связанных с необходимостью выбора оптимальной стратегии и перебором большого количества вариантов.

К числу таких задач относятся, в частности, нахождение кратчайшего пути в транспортных или информационных сетях, поиск пути выхода из лабиринта, поиск вершин дерева, обладающих заданным свойством (на примере задачи обхода всех полей шахматной доски).

Рассмотрен один из численных методов решения краевой задачи Дирихле для уравнения Лапласа, приведена программа построения картины стационарного плоского поля в прямоугольной области. В качестве инструментальных средств использованы система Delphi и математический пакет Mathcad.

Указания предназначены для выполнения контрольных работ по дисциплине «Математическое моделирование систем и процессов» специальности 190901 «Системы обеспечения движения поездов» студентов очной и заочной форм обучения.

Утверждены на заседании кафедры «16» октября 2012 г., протокол № 2. Печатаются по решению редакционно-издательского совета университета.

Составители: Ахмадуллин Ф.Р. Волик В.Г. Гуменников В.Б.

Рецензенты: д.т.н., проф., заведующий кафедрой «МАП» СамГУПС О.А. Кацюба; к.т.н., проф. кафедры «АТС » СамГУПС В. Б. Леушин.

Под редакцией авторов Компьютерная верстка: Е.А. Самсонова

Подписано в печать 21.12.2012. Формат 60×90 1/16. Усл. печ. л. 2,25. Заказ 301.

© Самарский государственный университет путей сообщения, 2012

2

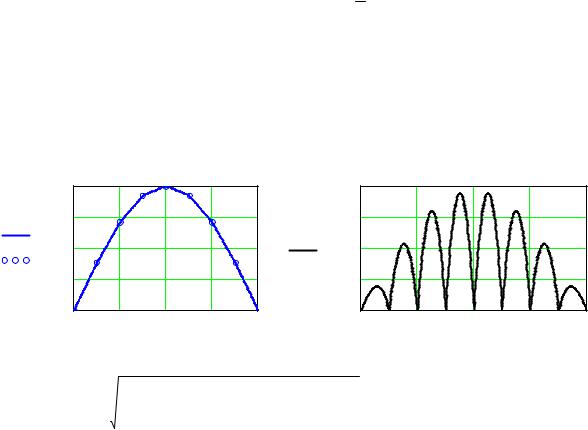
Работа 1. Аппроксимирующие методы формирования гармонических сигналов
				средствами математического пакета Mathcad
Задание 1. Осуществить кусочно-линейную интерполяцию функции													y = sin( π*x)					на отрезке
0 < x < 1 с помощью встроенной функции linterp(X,Y,x):
Задание интервала и числа участков:								time_range := 1							N := 8		j := 0.. N
Дискретизация аргумента и функции:								T	j	:=	j		U	j	:= sin(π T )
											N							j
Получение интерполяцирующей функции:								FKL1(t) := linterp(T , U , t)
Оценка погрешности интерполяции:								ERK(t) := sin(π t) − FKL1(t)
					Значения элементов векторов					T и U:
stack(T	T	T	0.0000		0.1250	0.2500	0.3750	0.5000		0.6250		0.7500				0.8750		1.0000
		, U )	=	0.0000	0.3827	0.7071	0.9239	1.0000		0.9239		0.7071				0.3827		0.0000
		Кусочно-линейная интерполяция								Абсолютная погрешность интерполяции
		1							0.02
FKL1(t)0.75								0.015
U		0.5						ERK(t)	0.01
		0.25						0.005
		0	0	0.25	0.5	0.75	1			0	0		0.25			0.5		0.75		1
					t, T											t
					Среднеквадратическая погрешность аппроксимации:

1			⌠1	(	(		))2		− 3
						π t		dt = 9.9207 × 10
time_range			⌡		FKL1(t) − sin
			0

Задание 2. Реализовать функции sin( π*x) и cos(2*π*x) на отрезке x = 0..0.5 методом интегрирования кусочно-линейной интерполирующей функции, заданной координатами пяти узловых точек. Вычислить среднеквадратическую погрешность аппроксимации.

Задание координат точек сопряжения ломаной			XY :=	0.0		0.125		0.25		0.375	0.5	T
линии, аппроксимирующей исходную функцию:						0.7071		1.0		0.7071	0.0
				0.0
Уравнение прямой,	FLine(x, x1	, y1	, x2, y2)	:=		a ←	y2 − y1
проходящей через две точки:
							x2 − x1
						b ← y1 − a x1
						a x + b

Уравнение кусочно-линейной функции, узлами которой является множество заданных точек:

FKL2(x, XY) :=				X ← XY 0
				Y ← XY 1
				N ← rows(XY) − 1
				return	Y0	if	x < X0
				return	YN	if	x ≥ XN
				for k 1.. N
				return FLine(x, Xk−1 , Yk−1 , Xk , Yk) if x < Xk

3

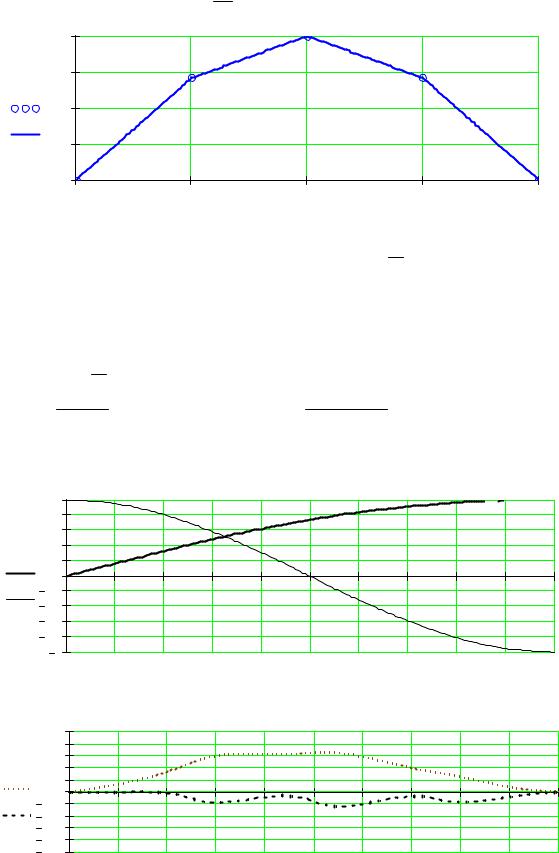
Формирование массива значений кусочно-ломаной аппроксимирующей функции:

n := 200

i := 0.. n

x := 0.5

Xi :=

x i

Yi := FKL2(Xi, XY)

n

1

1 0.75

XY

0.5

Y

0.25

0

0.13

0.25

0.38

0.5

XY 0 , X

n

Yj

n

Вычисление нормирующих множителей:

sn :=

cn :=

∑

∑

j

Yj

sn = 1.7367

cn = 120.7100

j = 0

j = 0

Формирование массивов аппроксимирующих функций:

S = sin(π*x);

C = cos(2*

π*x);

x = 0..0.5;

i

Yjj

i

∑

2

∑ Yj

Si :=

j = 0

Ci := 1 −

j = 0

sn

cn

Оценка погрешности аппроксимации:

ERSi := Si − sin(π Xi)

ERCi := Ci − cos(2 π Xi)

Графики аппроксимирующих функций:

1

0.8

0.6

S

0.4

0.2

C

0.2

0

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.4

0.6

0.8

1

X, X

Графики функций абсолютной погрешности аппроксимации:

0.05

0.04

0.03 ERS 0.02 0.01

ERC	0.01	0	0.05	0.1	0.15	0.2	0.25	0.3	0.35	0.4	0.45	0.5
	0.02
	0.03
	0.04
	0.05
							X, X
Среднеквадратическая									Stdev(ERC) = 3.5725 × 10− 3
погрешности аппроксимации:					Stdev(ERS) = 0.0117

4

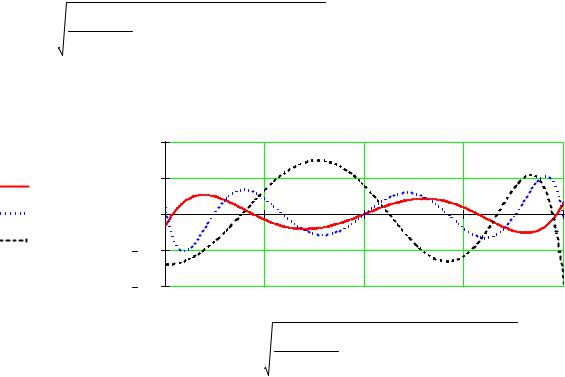
Задание 3. Аппроксимировать гармоническую функцию cos( π*x) в интервале x = 0 .. 1 с помощью полиномиальной регрессии и полиномиальным рядом Чебышева.

Вычислить среднеквадратическую погрешность аппроксимации.

	Число участков аппроксимации:							n := 12		j := 0.. n				j		Uj := cos(π Tj)
	Формирование массивов значений аргумента									и функции:		Tj :=
														n
	Значения координат узловых точек:
		( T	T)
	stack			=		0	1	2	3	4	5	6	7			8
					0	0.000	0.083	0.167	0.250	0.333	0.417	0.500	0.583			0.667
		T	, U
					1	1.000	0.966	0.866	0.707	0.500	0.259	0.000	-0.259			-0.500

Вычисление коэффициентов линейной регрессии с помощью встроенных функций: a := intercept(T , U) b := slope(T , U) a = 1.1653 b = −2.3306

Вычисление коэффициентов полиномиальной регрессии: FR(k) := regress(T , U , k) Формирование матрицы коэффициентов (для визуализации):

FRK(k) := submatrix(FR(k) , 3 , k + 3 , 0 , 0)

Получение аппроксимирующей функции: FUT(t , k) := interp(FR(k) , T , U , t)

Значения коэффициентов аппроксимирующего многочлена в зависимости от его степени.

	0.0000		0.0000	0.0000	0.0000
	1.1653		−2.3306	0.0000	0.0000
T		1.1653	−2.3306	0.0000	0.0000
CK	=	0.9965	0.2164	−6.6285	4.4190
		0.9965	0.2164	−6.6285	4.4190
		1.0000	−6.3025 × 10− 3	−4.8305	−0.6152

CK :=				Y0 , 0 ← mean(U)
				for		j 1.. 5
					X ← FRK(j)
						for i 0.. 6
									Yi, j ← Xi if i ≤ j
									Yi, j ← 0		otherwise
				Y
0.0000										0.0000	0.0000
0.0000										0.0000	0.0000
0.0000										0.0000	0.0000
0.0000										0.0000	0.0000
5.0704 × 10						− 15				0.0000	0.0000
5.7534										−2.3013	0.0000

	1	⌠1		Среднеквадратическая погрешность аппроксимации
FEP(k) :=				FEP(3) = 3.2853 × 10− 3		FEP(5) = 5.2383 × 10− 5
		(FUT(t , k) − cos(π t))2 dt
	time_range	⌡
		0
		Аппроксимация полиномиальным рядом Чебышева:				3
	A := ( 0.99858 0		−4.88779 0 3.81908 0		−0.93183 )T	FCH(x) := ∑ A2 i x2i
			Абсолютная погрешность аппроксимации			i = 0
		0.02
FUT(t, 4)−cos(π t)		0.01
(FUT(t, 6)−cos(π t))100
(FCH(t)−cos(π t))10		0	0.25	0.5	0.75	1
		0.01
		0.02
				t
Среднеквадратическая погрешность			1	⌠1
аппроксимации полиномиальным				(FCH(t) − cos(π t))2 dt = 9.7729 × 10− 4
	рядом Чебышева:		time_range	⌡
				0

5

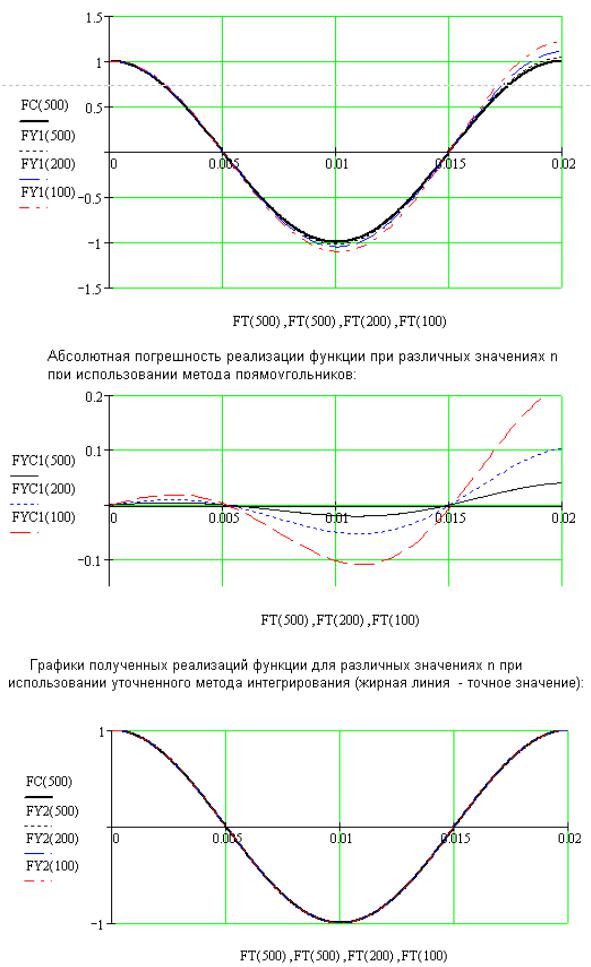
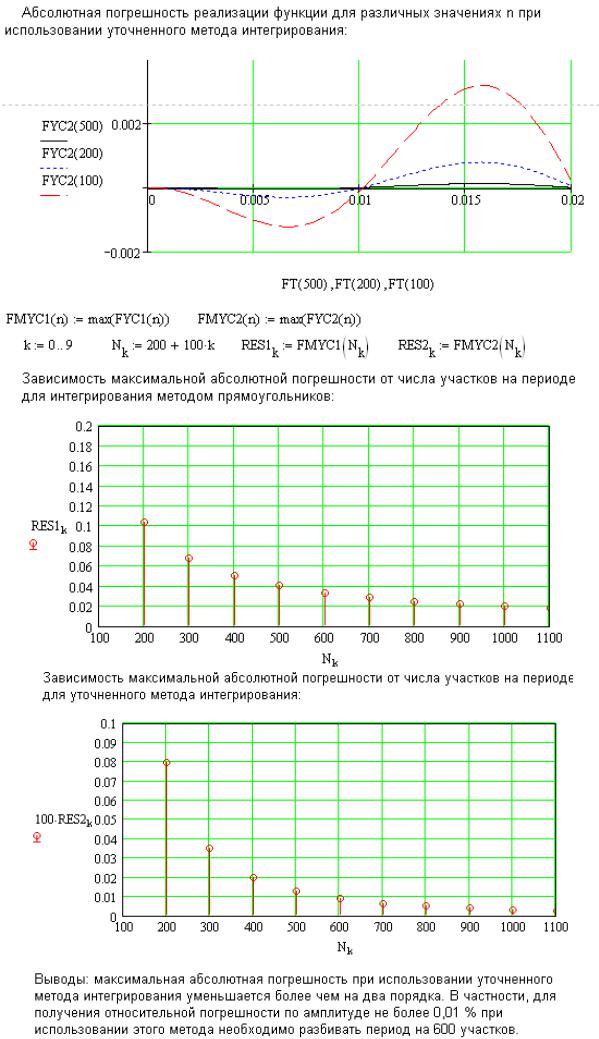
Работа 2. Получение гармонического сигнала методом численного интегрирования

Исходное дифференциальное уравнение:

∂2 y + y = 0 . ∂x2

Начальные условия:

y(0) = A٠cos(ψ); y’(0) = А· sin(ψ).

6

7

8

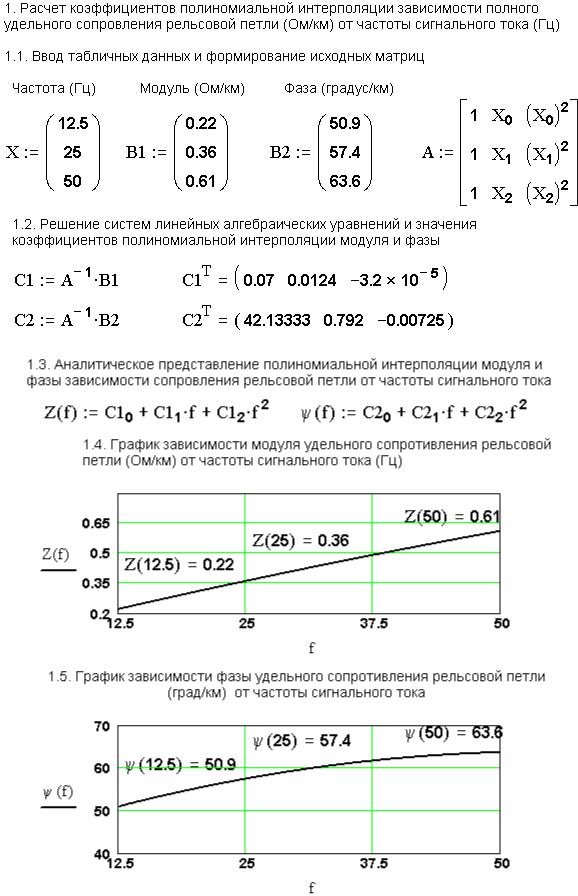
Работа 3. Программа расчета амплитуды сигнального тока на питающем конце рельсовой линии и параметрической чувствительности датчика координаты

взависимости от частоты напряжения, положения шунта и проводимости изоляции средствами пакета Mathcad

9

Исходные данные:

Максимальная длина рельсовой линииxm := 3.0 км	E := 4 В
Амплитуда напряжения источника сигнального тока		ke := 0.02
Коэффициент сопротивления подводящих проводов	кe( = ze/z0)

2. Функция расчета комплексной амплитуды сигнального тока на питающем конце рельсовой линии в зависимости от положения шунта x, удельной проводимости изоляции g0, частоты питающего напряжения f и коэффициента сопротивления шунта kh

										π
I2a(x, g0, f , kh) :=	z0 ←				Z(f) exp j ψ (f)
										180
	ze ← ke z0
	zh ← kh z0
	zv ←							z0
								g0
	γ ←					z0 g0
	z ←			cosh(γ x) zh + zv sinh(γ x)
						sinh(γ x)			zh + cosh(γ x)
								zv
			E
			ze + z

3.Результаты расчетов.

3.1.График амплитуды сигнального тока на питающем конце рельсовой линии в зависимости от положения шунта x ( на интервале от 2 до 3 км) при

фиксированных значенияхчастоты питающего тока ( f = 12, 25, 37 Гц )

иследующих значенияхпараметров рельсовой цепи:

-удельная проводимость изоляции ( g0 =1 Сим/км ),

-коэффициент сопротивления шунта ( кh = zh/z0 = 0.05 )

				12
I2a(x, 1 , 12 , 0.05)				10
I2a(x, 1 , 25 , 0.05)				8
I2a(x, 1 , 37 , 0.05)
				6
				4
					2		2.2		2.4		2.6		2.8								3
											x

10