
1579-Зубарев,Кайдалова
.pdf
1579
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПУТЕЙ СООБЩЕНИЯ
|
|
|
САМАРСКАЯ |
ГОСУДАРСТВЕННАЯ |
|
СамГАПС |
|||
|
АКАДЕМИЯ |
ПУТЕЙ СООБЩЕНИЯ |
||
|
|
|
|
|
|
|
|
|
|
К а ф е д р а в ы с ш е й м а т е м а т и к и
В Ы С Ш А Я МАТЕМАТИКА
Т Р Е Н И Р О В О Ч Н Ы Е Т Е С Т Ы
Д Л Я С Т У Д Е Н Т О В и н ж е н е р н о - т е х н и ч е с к и х и
э к о н о м и ч е с к и х с п е ц и а л ь н о с т е й
|
y |
|
|
B2 |
M(x, y) |
b |
|
|
|
|
|
F1(–c, 0) A1 |
O |
A2 F2(c, 0) x |
|
B1 |
a |
Cамара – 2005
УДК 519.7
Высшая математика. Тренировочные тесты для студентов инженер- но-технических и экономических специальностей / А.П. Зубарев, Л.В. Кайдалова; Самара: СамГАПС, 2005. 28 с.
Утверждена на заседании кафедры, протокол № 10 от 27.06.05.
Печатается по решению редакционно-издательского совета академии
Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике для технических и экономических специальностей и охватывают основные разделы курса высшей математики.
В методических указаниях приведены примеры решения тестовых задач, а также тест для самопроверки.
Предназначены для студентов инженерно-технических и экономических специальностей дневной формы обучения.
Ил. 25. Табл. 3. Библиогр.: 6 назв.
Составители: |
А.П. Зубарев, к. ф.-м. н., доцент, |
|
|
Л.В. Кайдалова, к. ф.-м. н., доцент, |
|
Рецензенты: к. т. н., доц. СамГТУ |
Егорова Г.Ф., |
|
|
к. т. н., проф. СамГАПС |
Герасимов В.А. |
Зубарев А.П., Кайдалова Л.В.
Самарская государственная академия путей сообщения, 2005
2

В В Е Д Е Н И Е
Тесты предназначены для использования в процедурах подготовки и самопроверки студентов с целью оценки уровня остаточных знаний по курсу «Математика».
Уровень сложности заданий и их содержание соответствует требованиям ГОС по математике для студентов инженерно-технических и экономических специальностей.
Т Р Е Н И Р О В О Ч Н Ы Й Т Е С Т |
С Р Е Ш Е Н И Я М И П О |
К У Р С У « М А Т Е М А Т И К А » |
|
№ |
З А Д А Н И Е |
Р Е Ш Е Н И Е |
|
|
|
|
|
|
|
Вычислим определитель разложением |
|||||||||||
|
|
|
|
|
|
|
по элементам второго столбца и далее по |
|||||||||||
|
|
|
|
|
|
|
элементам третьего столбца |
|
|
|
|
|||||||
|
Вычислить |
определи- |
|
1 |
0 |
4 |
3 |
|
1 |
4 |
3 |
|
|
|
||||
|
|
|
|
|
||||||||||||||
|
|
1 0 4 3 |
|
|
2 3 5 1 |
= 3 |
1 2 0 |
|
|
|
||||||||
1. |
тель |
2 |
3 |
5 |
1 |
. |
|
1 |
0 |
2 |
0 |
|
3 |
5 |
0 |
|
|
|
|
|
1 |
0 |
2 |
0 |
|
|
3 |
0 |
5 |
0 |
|
|
|
|
|
|
|
|
|
3 |
0 |
5 |
0 |
|
|
|
= 9(1 5 3 2) 9 . |
|
||||||||
|
|
|
|
|
|
|
Замечание. Разложение надо осущест- |
|||||||||||
|
|
|
|
|
|
|
влять по строке (столбцу), содержащей |
|||||||||||
|
|
|
|
|
|
|
наибольшее количество нулей. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
Найдем решение системы. Для этого из |
|||||||||||
|
|
|
|
|
|
|
второго уравнения отнимем первое, по- |
|||||||||||
|
Найти x0 – y0, если (x0, |
лучим уравнение относительно х и ре- |
||||||||||||||||
|
y0) – решение системы |
шим его: |
|
2x 8 x 4 . |
Подставим |
|||||||||||||
2. |
линейных уравнений |
полученное значение в первое уравнение |
||||||||||||||||
|
|
x 2y 3; |
системы |
и |
получим: |
|
4 2y 3 |
|
||||||||||
|
|
|
|
|
|
|
y 3,5 . Таким образом, x0 = 4, у0 = –3,5 |
|||||||||||
|
|
3x 2y 5. |
||||||||||||||||
|
|
|
|
|
|
|
x0 – y0 = 7,5. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |

№ |
|
З А Д А Н И Е |
|
|
|
|
|
|
|
|
|
|
|
|
Р Е Ш Е Н И Е |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
4 |
|||||||
|
|
Если |
|
A |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
Найдем сначала 2А: 2А = |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
8 |
|
|
|
. |
|||||||||||||||||||||||||||||
3. |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
3 |
||||||||||||||
|
B |
|
|
|
|
|
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Далее вычислим С = 2А + В = |
8 |
|
|
|
. |
||||||||||||||||||||||||||||||||||||
|
С = 2А + В имеет вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Протранспонируем матрицу А, т. е. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строки |
заменим |
столбцами |
(с |
теми |
|
же |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
номерами) |
|
|
|
|
|
|
|
|
|
|
Умножение |
||||||||||||||||||||||||
|
Вычислить D |
= A |
C, |
где |
A |
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
возможно, |
поскольку |
|
число |
столбцов |
||||||||||||||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. |
|
2 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
первой матрицы равно числу строк вто- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|
рой; в результате умножения получается |
|||||||||||||||||||||||||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
1 |
2 |
|||||||
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
матрица порядка 2 2 A C |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
1 |
|
5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
5 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Уравнение |
линии |
на |
|
|
|
|
Уравнение прямой, проходящей через |
||||||||||||||||||||||||||||||||||||||||||||||||
|
рисунке имеет вид… |
|
|
|
две точки (х1, |
у1) и (х2, у2), имеет вид |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
x x1 |
|
|
y y1 |
|
|
x 1 |
|
y 0 |
|
|
y = |
||||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 y1 |
|
|
|
0 1 |
|
|
|
2 0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2x + 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
– |
|
1 |
0 |
|
x |
|
|
|
|
|
|
|
|
|
Замечание. Можно проверить, какому |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
уравнению |
из |
ответов |
|
|
удовлетворяют |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
координаты точек (–1, 0) и (0, 2). |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
Найти |
|
|
координаты |
|
и |
|
|
|
|
|
|
|
|
|
|
|
= 4, |
5, 3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
6. |
|
|
|
|
|
|
A1A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A1A2 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
длину вектора |
A1A2 , если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
4 2 52 |
3 2 |
|
|
|
|
|
5 |
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||||||||||||||
|
А1(4, 2, 5), А2(0, 7, 2). |
|
|
|
|
|
|
|
50 |
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2i 6 j 3k |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 ( 6)2 32 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
a |
|
|
49 7 . |
|
|
||||||||||||||||||||||||||||||||||||||||||
то |
|
|
|
=... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Векторы |
|
|
|
|
= (3, 2k, 5) |
|
|
|
|
Условие |
|
|
|
|
перпендикулярности |
||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
0 |
|
|
axbx ayby |
azbz 0 |
|
3(– |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
b |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
8. |
|
|
a |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
и b = (–3, 1, 2) перпенди- |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
3) + 2k + 5 2 = 0 k = –0,5. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
кулярны, если k = … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
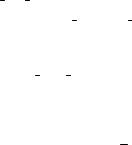
№ |
|
|
|
З А Д А Н И Е |
|
|
|
|
|
|
|
|
|
|
Р Е Ш Е Н И Е |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Векторы |
|
|
|
|
(3, 2 , 5) |
|
|
|
Условие |
|
|
|
|
|
|
|
|
|
|
|
|
коллинеарности |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
ax |
|
|
ay |
|
|
|
az |
|
|
3 |
|
|
2 |
|
|
5 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
и b (–3, 1, ) |
коллине- |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
bx |
by |
|
|
bz |
3 |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
арны, если = …, = … |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
= –0,5; = –5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
2 |
1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
2, 3, 1 ; |
|
0, 1, 5 . |
a b |
2 3 |
1 |
i |
|
|
|
j |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
b |
1 |
|
|
5 |
|
|
|
0 |
|
|
|
5 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
10. |
Векторное |
произведение |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
векторов |
a |
|
b |
|
равно … |
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
k |
|
|
|
16i 10 j 2k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальный вектор плоскости |
|
|
име- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
Нормальный |
вектор |
|
|
|
n |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ет координатами коэффициенты при x, y, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
11. |
плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z в уравнении плоскости |
n |
(A, B,C) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
х + 2у + z – 15 = 0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
имеет координаты… |
|
|
(1, 2, 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
Из уравнений а) 2x – |
|
|
|
Уравнение |
|
|
плоскости, параллельной |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3y + z + 1 = 0; б) x + 2y – 6 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
12. |
= 0; в) x + 3y = 0 выбе- |
оси Oz, имеет коэффициент при z равный |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
рите те, которые опреде- |
0 C 0 Ax By D 0 |
случаи |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ляют плоскость, парал- |
б) и в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
лельную оси Oz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Угловой |
коэффициент |
|
|
|
В уравнении прямой |
|
y kx b |
|
k – уг- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
k и величина |
|
|
отрезка b, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ловой коэффициент, b – величина отрез- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
13. |
отсекаемого |
|
|
|
|
|
|
|
|
прямой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ка, отсекаемого прямой на оси Oy. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x 2 y 6 0 |
на оси Oy, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
равны… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x / 2 3 |
|
k = –0,5; b = –3. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Если уравнение гипер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
болы имеет вид |
|
|
|
|
|
x2 |
|
|
y2 |
|
|
|
(a 0, b 0) |
|
|
– уравнение |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 |
|
y2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
14. |
|
|
|
|
|
|
|
|
1 , |
|
|
|
|
a2 |
b2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
гиперболы, где а – действительная полу- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
то длина ее действитель- |
ось, b – мнимая полуось а = 2. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ной полуоси равна… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
Уравнение |
|
|
|
|
|
|
|
Дополним уравнение до полного квад- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
рата 2(x |
2 |
|
+ x / 2 + 1 / 16) + 2y |
2 |
= 1 / 8 2(x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2x |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
15. |
|
|
|
|
|
+ 2y + x = 0 |
|
|
|
|
|
|
2 |
|
|
|
2 |
= 1 / 8 (x + 1 / 4) |
2 |
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
определяет |
|
|
на |
плоско- |
+ 1 / 4) |
|
|
+ 2y |
|
|
+ y = 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
сти… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/ 16 |
|
окружность с центром О(–1 / 4; 0) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и радиусом R = 1 / 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
5
№ |
З А Д А Н И Е |
|
|
|
|
|
|
Р Е Ш Е Н И Е |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Радиус окружности, |
за |
|
|
Дополним уравнение до полного квад- |
|||||||||||||||||||||||||||||||||||||||||||||||||
16. |
данной уравнением |
|
|
рата |
|
|
|
|
|
(x |
2 |
2x 1) (y |
2 |
2y 1) 9 , |
||||||||||||||||||||||||||||||||||||||||
х2 – 2х + у2 + 2у – 7 = 0, |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
(x 1)2 (y 1)2 |
9 |
|
О(1; –1), R = 3. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
равен… |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Образ вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
y Ax |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
в базисе линейного опе- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 4 |
|
|||||||||||||||||||||||||
ратора, |
заданного матри- |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
имеет |
|
12 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
цей A |
4 |
5 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем |
основные |
|
виды |
|
уравнений |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
поверхностей |
|
|
|
|
второго |
|
|
|
|
|
|
|
|
порядка |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
y2 |
|
|
z2 |
|
1 |
|
|
|
|
|
– |
|
|
|
|
|
|
|
эллипсоид, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
z2 |
|
1 – однополостной гипер- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
b2 |
c2 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
болоид, |
|
x2 |
|
|
y2 |
|
z2 |
1 – двуполостной |
||||||||||||||||||||||||||||||||||
|
Геометрический |
образ |
|
a2 |
|
b2 |
c |
2 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
гиперболоид, |
|
|
z |
x |
2 |
|
y |
2 |
|
|
|
– |
|
эллиптиче- |
|||||||||||||||||||||||||||||||||||||||
|
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
18. |
|
x2 |
|
y2 |
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
ский параболоид, z |
x |
2 |
|
|
y2 |
|
– гипербо- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
5 |
|
|
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
2 |
|
b2 |
||||||||||||||||||||||||||||||||||||||||||||
|
имеет вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
лический параболоид, |
|
|
|
|
1 |
|
– эл- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
липтический цилиндр, |
|
x2 |
|
y2 |
|
|
|
1 |
– ги- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
перболический цилиндр, |
|
y2 2px |
|
– па- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
раболический цилиндр, |
|
|
|
x2 |
|
|
y |
2 |
|
|
z |
2 |
0 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
c2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
– конус в данном случае конус. |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
Какие арифметические |
|
|
Множество |
|
|
натуральных |
|
|
|
|
|
чисел |
|||||||||||||||||||||||||||||||||||||||||
19. |
действия |
(сложение, ум- |
|
N {1, 2, 3,...} |
только сложение и ум- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
ножение, |
вычитание, |
де- |
ножение, так как при вычитании появля- |
||||||||||||||||||||||||||||||||||||||||||||||||||
6
№ |
З А Д А Н И Е |
|
|
|
Р Е Ш Е Н И Е |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ление) |
справедливы для |
ются отрицательные числа, а при делении |
||||||||||||||||||||||||||||||||||||||
|
множества |
|
натуральных |
– дробные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
чисел? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На диаграмме Эйлера- |
|
|
|
|
А \ В |
|
|
|
|
|
А В или В А |
|
|
|
|
|||||||||||||||||||||||||
|
Венна приведена геомет- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
А |
|
|
|
|
|
|
|
||||||||||||||
|
рическая |
|
|
|
иллюстрация |
|
|
|
|
|
А |
|
|
|
|
|
|
|
В |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
20. |
понятия… |
|
|
|
|
|
|
|
|
А В или A + B |
А В или А В |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
А |
|
|
|
|
|
||||||||
|
|
|
|
А |
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А \ В. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пересечением множеств А и В называ- |
|||||||||||||||||||||||||||||
|
Пересечение множеств |
ется множество, образованное из всех тех |
|||||||||||||||||||||||||||||||||||||||
21. |
А = {1, 3, 5, 10} и В = {3, |
элементов, которые принадлежат и мно- |
|||||||||||||||||||||||||||||||||||||||
|
5, 7} равно… |
жеству А, и множеству В A B = {3, |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На |
числовой прямой |
-окрестностью точки |
х0 |
служит ин- |
||||||||||||||||||||||||||||||||||||
|
дана точка |
|
х = 5,6. Тогда |
||||||||||||||||||||||||||||||||||||||
22. |
ее |
« -погрешностью» |
тервал x0 ; x0 |
|
интервал должен |
||||||||||||||||||||||||||||||||||||
может являться интервал |
быть |
симметричен |
|
относительно |
х |
||||||||||||||||||||||||||||||||||||
|
а) (5,6; 5,8), б) (0, 6), |
(5,4; 5,8) ответ в). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
в) (5,4; 5,8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
23. |
Функция |
|
|
y log3 x |
Это монотонно возрастающая функция |
||||||||||||||||||||||||||||||||||||
отображает |
|
множество |
f(0) = – ; f (27) = 3 (– , 3]. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
(0; 27] на множество... |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Это |
|
|
немонотонная |
|
|
|
|
y |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
функция на промежутке |
|
|
|
5 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у= х2–4 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Функция |
|
|
y x2 4 |
1;3 . Построим график |
|
|
|
–1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
24. |
отображает |
|
множество |
функции у = х2 – |
4. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Множество |
1;3 |
|
по |
–2 |
|
|
|
|
|
|
|
x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
2 3 |
|||||||||||||||||||||||||||||||||
|
1;3 на множество … |
оси Ох отображается на |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
множество [–4; |
5] |
по |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–4 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
оси Оу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Предел |
|
|
|
|
|
lim |
|
2x2 2 |
|
|
|
0 |
lim |
|
|
2(x 1)(x 1) |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2x |
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
25. |
lim |
|
|
x 1 3x |
|
9x 6 |
0 |
|
x 1 3(x 1)(x 2) |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2(x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 9x 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x 1 3x |
= lim |
4/ 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
равен… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x 1 3(x 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7
№ |
|
|
З А Д А Н И Е |
|
|
|
|
|
|
|
|
|
|
Р Е Ш Е Н И Е |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Предел |
|
lim |
|
|
|
|
ра- |
|
|
|
|
2x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
26. |
|
|
|
|
|
x x2 3 |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
0 . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
вен… |
|
|
|
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
x (x) |
|
x 2x |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Функция |
y |
x 2 |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
27. |
|
x 2 |
|
|
|
x 2 , так как |
lim |
|
0 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
бесконечно малая в точ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
ке… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Если |
|
|
z1 1 i , |
|
|
|
z |
|
z |
2 |
|
(1 i)(2 i) 2 2i i i2 , |
|
|
|
так |
||||||||||||||||||||||||||||||||||||||||||
28. |
z |
|
2 i , |
|
то |
z z |
|
рав- |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 z2 = 3 i . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
как |
i |
|
|
|
= –1, то |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
но… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Если |
f (z) 4z2 – |
4i, |
|
|
|
f (z) 8z |
|
|
|
f (2 2i) |
8(2 2i) = |
|||||||||||||||||||||||||||||||||||||||||||||||
29. |
тогда значение производ- |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ной этой функции в точке |
16 16i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
z0 2 2i |
равно… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
На |
рисунке |
представ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
лена |
геометрическая |
|
ил- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
люстрация |
комплексного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
числа |
z x iy . Тогда |
|
|
|
Тригонометрическая |
|
форма |
|
|
|
записи |
||||||||||||||||||||||||||||||||||||||||||||||||
|
тригонометрическая фор- |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
имеет вид |
|
|
|
|
z r(cos isin ) , |
|
|
|
где |
= |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
ма |
записи |
этого |
числа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
30. |
имеет вид… |
|
|
|
|
|
/ 4, |
|
|
|
r |
|
|
|
x2 y2 |
22 |
22 2 |
|
|
|
|
|
|
(см. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
y |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
рисунок) z = |
|
|
|
|
|
|
|
|
i sin |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
2 cos |
|
|
|
|
|
|
. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= /4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
x |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модуль |
|
|
|
|
|
|
|
и |
|
аргумент |
комплексного |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
числа |
|
|
|
|
определяются |
|
по |
формулам |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
Модуль и главное зна- |
|
z |
|
|
|
|
|
x2 y2 , |
|
arg z |
|
(см. рисунок из |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
31. |
чение |
аргумента |
|
ком- |
№ |
30). |
|
|
|
z |
|
|
|
|
( 4)2 |
|
02 |
4 . |
|
Так |
как |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
плексного |
|
числа |
z 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x r cos , |
|
|
y r sin , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|||||||||||||||||||||||||||||||||||||||
|
равны… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
0 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
1, |
sin |
|
0 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= . |
|
|
|
r |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
4 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8
№ |
З А Д А Н И Е |
|
|
|
|
|
|
|
|
Р Е Ш Е Н И Е |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексное число |
|
в |
|
показательной |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
форме |
|
|
имеет |
|
|
|
|
вид |
|
|
|
z r ei , |
где |
|||||||||||||||||||||||
|
Показательная |
форма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , cos |
x |
1/ 2, |
|||||||||||||||||||||||||||
|
|
|
z |
|
|
( 1)2 |
( |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
3)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
32. |
записи числа |
z 1 i |
|
|
3 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|||||||||||||
|
имеет вид… |
|
|
|
|
|
|
|
|
|
sin |
|
|
|
3 |
|
|
|
= |
2 / |
3. Тогда |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2ei2 / 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Производная |
функции |
|
|
|
|
|
|
|
|
2xsin x2 1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
33. |
y cos x2 |
1 |
имеет |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для |
|
|
|
|
|
|
функции |
|
|
|
|
|
y(0) 0 ; |
|
|
|
y 3x2 |
6x; |
y (0) |
0 ; |
|||||||||||||||||||||||||||||||
34. |
y x3 3x2 |
|
точка x = 0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
является точкой а) раз- |
|
y 6x 6 ; |
|
y (0) 6 0 |
|
x = 0 – точ- |
||||||||||||||||||||||||||||||||||||||||||||||
|
рыва; б) перегиба; в) ми- |
ка максимума ответ г). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
нимума; г) максимума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Укажите |
вид |
графика |
|
|
|
y > 0 график лежит выше оси Ох; |
|||||||||||||||||||||||||||||||||||||||||||||
|
функции, для которой на |
|
y 0 |
|
|
функция убывает; |
y 0 |
|
||||||||||||||||||||||||||||||||||||||||||||
35. |
всем отрезке [a; b] одно- |
выпуклая. Вид графика |
y |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
временно |
|
|
|
выполняются |
приведен на рисунке. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
условия |
y 0 , |
y 0 , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 a |
|
|
|
b x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Уравнение |
|
касатель- |
|
|
|
Уравнение |
|
|
|
|
|
|
|
|
|
касательной |
– |
||||||||||||||||||||||||||||||||||
|
ной к графику функции y |
|
y y0 |
f (x0 )(x x0 ) , у0 = 1, х0 = |
0 |
|||||||||||||||||||||||||||||||||||||||||||||||
36. |
= = |
1 |
|
|
в точке (0; |
1) |
|
|
|
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x3 1 |
|
f (x) |
|
|
|
|
|
, f (0) |
0 |
y 1 0 . |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x3 1)2 |
|
|||||||||||||||||||||||||||||||||||
|
имеет вид... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Частная |
|
|
|
|
производная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
функции |
z x4 cos y |
|
|
по |
|
z |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
37. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
sin y , |
|
|
|
|
|
|
|
|
|
sin / 2 = –1. |
|||||||||||||||||||
переменной |
|
|
y |
в точке |
|
|
|
|
|
|
|
y |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
М(1; / 2) равна… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Дан |
|
радиус-вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
движущейся в простран- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k , |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
38. |
стве |
точки |
R(t) 3t |
i |
|
|
|
|
v(t) R (t) 6t i j 3t |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
t j – t3 1 k , |
|
тогда |
век- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w(1) 6i 6k . |
|||||||||||||||||||||||||
|
|
|
w(t) v |
(t) 6i 6t k , |
||||||||||||||||||||||||||||||||||||||||||||||||
|
тор |
ускорения |
точки |
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
№ |
|
|
З А Д А Н И Е |
|
|
|
|
Р Е Ш Е Н И Е |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
момент |
времени |
t = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
имеет вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Градиент |
|
скалярного |
|
|
|
|
|
|
u |
|
u |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
поля u |
x |
xz yz |
в |
|
|
, , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
39. |
|
gradu |
x |
z |
= (2x –z; z; –x + y) |
||||||||||||||||||||||||||||||||||
точке |
А(0; |
1; |
1) |
имеет |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
gradu(A) ( 1; 1; 1) = i |
j |
k . |
|
|
||||||||||||||||||||||||||||||||||
|
вид… |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Производная |
скаляр- |
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
u |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
gradu |
|
, |
|
|
|||||||||||||
|
ного |
поля |
|
|
u x |
|
|
|
|
|
e gradu , |
|
|
|
|
|
|
= |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
y |
|
||||||||||||||||||||||||||||
|
+ 2yx 4y |
в точке |
|
C(– |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
40. |
|
= 2x 2y; 2x 4 , |
|
|
gradu(C) ( 4; 6) , |
||||||||||||||||||||||||||||||||||
|
1; –1) в направлении еди- |
|
|
||||||||||||||||||||||||||||||||||||
|
ничного |
|
|
|
вектора |
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
(1; 0) равна… |
|
|
|
|
|
|
(1, 0)( 4, 6) 4 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
e |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Это задача на условный экстремум. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Целевая функция – П = 0,25xy – x – y – 2 |
|||||||||||||||||||||||||||
|
|
|
Прибыль |
|
П |
автомо- |
max (*) при условии х + у + 2 |
27 |
|||||||||||||||||||||||||||||||
|
|
|
|
(**). Выразим из (**) х и подставим в (*): |
|||||||||||||||||||||||||||||||||||
|
бильного завода от про- |
х = 25 – у, П = 0,25(25 – у)y – 25 +у – y – |
|||||||||||||||||||||||||||||||||||||
|
изводства |
одного |
авто- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
мобиля |
|
определяется |
2, П = 6,25у – 0,25 у – 27 – функция од- |
|||||||||||||||||||||||||||||||||||
|
формулой П = 0,25xy – x |
ной переменной. |
Исследуем ее |
на |
|
экс- |
|||||||||||||||||||||||||||||||||
|
тремум: П = 6,25 – |
0,5у; П = |
0 |
|
у = |
||||||||||||||||||||||||||||||||||
|
– y – 2, где x – затраты на |
|
|||||||||||||||||||||||||||||||||||||
|
материалы, млн. р., (x > |
12,5; П = – 0,5 < 0 |
у = 12,5 – точка |
||||||||||||||||||||||||||||||||||||
|
0); у – затраты на оплату |
максимума. Тогда х = 25 – 12,5 = 12,5. |
|||||||||||||||||||||||||||||||||||||
41. |
рабочей силы, млн. р., (y |
Таким образом, значения x и y, при кото- |
|||||||||||||||||||||||||||||||||||||
рых прибыль завода максимальна, а сум- |
|||||||||||||||||||||||||||||||||||||||
|
> 0); 2 млн. р. – постоян- |
марные затраты на один автомобиль не |
|||||||||||||||||||||||||||||||||||||
|
ные затраты. |
Значения x |
превышают 27 млн. р. равны соответст- |
||||||||||||||||||||||||||||||||||||
|
и y, при которых прибыль |
||||||||||||||||||||||||||||||||||||||
|
венно х = 12,5; у = 12,5. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
завода |
максимальна, |
а |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Замечание. Эту задачу можно решить, |
|||||||||||||||||||||||||||||||||||||
|
суммарные |
|
затраты |
|
на |
|
|||||||||||||||||||||||||||||||||
|
один автомобиль не пре- |
проверив сначала, удовлетворяют ли |
|||||||||||||||||||||||||||||||||||||
|
предложенные варианты ответов ограни- |
||||||||||||||||||||||||||||||||||||||
|
вышают 27 млн. р. рав- |
чению (**), и далее подставить подходя- |
|||||||||||||||||||||||||||||||||||||
|
ны... |
|
|
|
|
|
|
|
|
щие варианты ответов в целевую функ- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
цию и выбрать среди них максимальное |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
значение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Множество |
|
первооб- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
42. |
разных функции |
|
|
|
|
|
F(x) = |
|
1 |
e |
6x 2 |
C . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
f (x) e |
6x 2 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
имеет вид… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10
