
2638 ЭИ
.pdf2638 |
Министерство транспорта Российской Федерации |
Федеральное агентство железнодорожного транспорта |
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
Кафедра высшей математики
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ для студентов первых курсов всех специальностей
очной формы обучения
Составители: Ю.В. Гуменникова О.Е. Лаврусь
Самара
2010
1
УДК 519.7
Элементы векторной алгебры : методические указания и задания для студентов первых курсов всех специальностей очной формы обучения / составители : Ю.В. Гуменникова, О.Е. Лаврусь. – Самара : СамГУПС, 2010. – 32 с.
Утверждены на заседании кафедры 15.09.2010 г., протокол № 2. Печатается по решению редакционно-издательского совета университета.
Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике и охватывают основные разделы векторной алгебры.
В методических указаниях приведены индивидуальные задания, необходимые теоретические сведения, а также примеры решения задач.
Предназначены для студентов 1-го курса всех специальностей очной формы обучения.
Составители: Ю.В. Гуменникова, к.ф.-м.н., доцент О.Е. Лаврусь, к.т.н., доцент
Рецензенты: к. ф.-м. н., доцент СамГУ Г.В. Воскресенская; к. ф.-м. н., доцент СамГУПС Л.В. Кайдалова
Под редакцией составителей
Подписано в печать 28.09.2010. Формат 60×90 1/16. Усл. печ. л. 2,0. Заказ № 225.
© Самарский государственный университет путей сообщения, 2010
2
1. Векторы
Вектором называется направленный отрезок. Если начало вектора находится в точке
A, а конец в точке B, то вектор обозначается AB :
B
A 
Если начало и конец вектора не указываются, то его обозначают строчной буквой
латинского алфавита – a , |
|
, c и т. д: |
|
|
|
b |
|
|
|
||
|
|
a |
|
|
c |
|
|
b |
|||
Направление вектора |
|
изображается |
стрелкой. Через BA обозначается вектор, |
||
направленный противоположно AB , через − a вектор, направленный противоположно a .
|
B |
B |
|
A |
A |
a |
− a |
|
|
Вектор, у которого начало и конец совпадают, называется нулевым и обозначается 0 . Длиной, или модулем вектора, называется расстояние между его началом и концом.
Записывается AB или a , соответственно.
Векторы называются коллинеарными, если они параллельны одной прямой, и компланарными, если они параллельны одной плоскости.
Два вектора называются равными, если они коллинеарны, одинаково направлены и равны по длине.
Два вектора называются ортогональными, если они перпендикулярны друг другу. Свободным вектором в пространстве называется вектор, который без изменения
дины и направления может быть перенесен в любую точку пространства.
2.Линейные операции над векторами
Клинейным операциям над векторами относятся: умножение вектора на число и сложение (вычитание) векторов.
Произведением вектора a на число m называется вектор ma , направление которого совпадает с направлением вектора a , если m > 0 и противоположно ему, если m < 0.
Длина вектора обозначается m a или ma . Например:
2a
a
− 3a
3

Сумму (разность) двух свободных векторов можно найти по правилу параллелограмма.
Пример. Даны свободные векторы a и b :
a b
Поместим их начала в одну точку и достроим до параллелограмма:
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
d |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
||||||
Тогда вектор |
|
= a |
+ |
|
направлен по диагонали, берущей начало из этой же точки, а |
|||||||||||||
c |
b |
|||||||||||||||||
вектор |
|
= a – |
|
|
|
будет направлен по |
другой диагонали параллелограмма от |
|||||||||||
d |
b |
|||||||||||||||||
вычитаемого к уменьшаемому.◄ Если векторов больше двух, то применяют правило многоугольника, согласно
которому векторы помещают последовательно (начало последующего помещается в конец предыдущего), а суммой векторов будет являться вектор, начало которого находится в начале первого вектора, а конец – в конце последнего вектора.
Пример. Даны векторы a , b , c :
a b c
c
Найти линейную комбинацию d = 2a − b + 3c . Решение. Найдем векторы 2 a , – b , 3 c :
2a
− b
3c
Применив правило многоугольника, получаем
− b
3c |
2a |
d
4
3. Проекция вектора на ось. Координаты вектора
Если взять ось l и вектор a и опустить перпендикуляр из конца вектора a на ось l, то получим отрезок MN, который является проекцией вектора a на ось l.
Итак, проекцией вектора a на ось l называется число, обозначаемое прl a и равное 
 , где ϕ – угол между положительным направлением оси l и направлением вектора a (длина отрезка MN).
, где ϕ – угол между положительным направлением оси l и направлением вектора a (длина отрезка MN).
Если свободный вектор a перенести в координатное пространство систему координат) Oxyz, то он может быть представлен в виде
a = ax i + ay j + az k .
a
φ 
M N l
(декартову
z 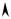
az 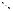

|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
j |
|
ay |
|
|
|
0 |
|
|
|
y |
||||
i |
|
|
|
|||||||
ax 

















x
Такое представление вектора a называется его разложением по осям координат или
разложением по ортам.
Здесь ax, ay, az – проекции вектора a на соответствующие оси координат (их называют координатами вектора a ); i , j , k – орты этих осей (единичные векторы, направление которых совпадает с положительным направлением соответствующей оси).
Векторы axi , ay j , az k , в виде суммы которых представлен вектор a , называются
составляющими (компонентами) вектора a по осям координат. Применяется также запись
a = (ax, ay, az).
Длина (модуль) вектора a обозначается a и определяется по формуле
a = 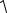 ax2 + a2y + az2 .
ax2 + a2y + az2 .
5

Направление вектора a определяется углами α, β, γ, образованными вектором a с осями координат Ox, Oy, Oz. Косинусы этих углов (так называемые направляющие косинусы вектора) определяются по формулам:
|
|
|
|
|
|
|
|
cosα = |
ax |
= |
ax |
|
|
|
|
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
ax2 + ay2 + az2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
cos β = |
ay |
= |
ay |
|
|
|
|
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
ax2 + ay2 + az2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
cosγ = |
az |
= |
az |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
a |
ax2 + ay2 + az2 . |
|||||||||||||||
Направляющие косинусы вектора связаны соотношением |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cos2 α + cos2 β + cos2 γ = 1 . |
||||||||||||||||
Если векторы |
a и |
|
|
|
заданы их разложениями по ортам, то их сумма и разность |
|||||||||||||||||||
b |
||||||||||||||||||||||||
определяются по формулам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
a + |
|
|
= (ax + bx )i |
+ (a y + by ) |
|
|
|
+ (a z + bz )k |
, |
||||||||||||||
|
b |
|||||||||||||||||||||||
|
j |
|||||||||||||||||||||||
|
a − |
|
= (a x − bx )i |
+ (a y − by ) |
|
+ (a z − bz )k |
. |
|||||||||||||||||
|
b |
|||||||||||||||||||||||
|
j |
|||||||||||||||||||||||
Произведение вектора a на скалярный множитель m определяется по формуле |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+ ma y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ maz k |
. |
|||||||||||
|
|
|
|
|
|
|
ma = maxi |
j |
||||||||||||||||
В частности, |
если |
m = 1 |
, то вектор |
a |
|
имеет длину, равную единице, и |
||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
||
направление, совпадающее с направлением вектора a . Этот вектор называют единичным вектором (ортом) вектора a и обозначают a0 . Нахождение единичного вектора того же направления, что и данный вектор a , называется нормированием вектора a .
Вектором ОМ , начало которого находится в начале координат, а конец – в точке M(x, y, z) называют радиус-вектором точки M и обозначают r (M) или просто r . Так как его координаты совпадают с координатами точки M, то его разложение по ортам имеет вид
r = xi + yj + zk .
Вектор AB , имеющий начало в точке A(x1, y1, z1) и конец в точке B(x2, y2, z2) может быть записан в виде AB = r2 − r1, где r 2 – радиус-вектор точки B, а r 1 – радиус-вектор точки A. Поэтому разложение вектора AB по ортам имеет вид
AB = (x2 − x1 )i + (y2 − y1 ) j + (z2 − z1 )k .
4. Деление отрезка в данном соотношении
Пусть на произвольной прямой задан отрезок AB. Тогда всякая точка C этой прямой делит отрезок AB в некотором отношении λ = ± |AC|:|CB|. Если отрезки AC и CB
6

направлены в одну сторону (т.е. точка C лежит внутри отрезка AB), то λ приписывают знак «+». Если же отрезки AC и CB направлены в противоположные стороны (т.е. точка C лежит вне отрезка AB), то λ приписывают знак «–».
Если точка A имеет координаты (x1, y1, z1), а точка B – координаты (x2, y2, z2), то координаты точки C ( x , y , z ) определяются по формулам:
x = |
x |
|
+ λx |
2 |
; |
|
y = |
y1 + λy2 |
; |
|
z = |
z + λz |
2 |
. |
||||
|
1 |
+ λ |
|
1 + λ |
|
1+ λ |
||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
В частности, если точка C делит отрезок AB пополам, то λ = 1 и координаты точки |
||||||||||||||||||
C( x , y , z ) определяются по формулам: |
|
|
|
|
|
|
|
|
|
|
||||||||
x = |
x1 + x2 |
; |
y = |
y1 + y2 |
; |
z = |
z1 + z2 |
. |
|
|
||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
||
5. Скалярное произведение векторов и его приложения
Скалярным произведением двух векторов a и b называется число c = a b , равное произведению данных векторов на косинус угла между ними
a b = a b cos(a b ),
где (a^b ) обозначает меньший угол между направлениями векторов a и b , причем всегда 0 ≤ (a ^ b )≤ π .
Свойства скалярного произведения векторов:
1)a b = b a ;
2)(λ a ) b = λ (a b )= a (λ b );
3)a (b + c )= a b + a c ;
4) a b = a npa b = b npb a ;
5)a a = a 2 ;
6)a ·b = 0 ↔ a b , т.е. если ненулевые векторы ортогональны.
Если векторы a и b разложены по осям координат, т. е. a = (ax , ay , az ) и b = (bx , by , bz ), то скалярное произведение находится по формуле
a b = ax bx + a y by + az bz ,
т. е. сумме произведений соответствующих координат.
С помощью скалярного произведения можно определить угол между векторами:
cos(a ^ |
|
)= |
a b |
= |
ax bx + a y by + az bz |
. |
b |
||||||
|
|
|
a b |
|
ax2 + a 2y + az2 bx2 + by2 + bz2 |
|
Работа A силы F , произведенная этой силой при перемещении тела на пути |S|, определяемом вектором S , вычисляется по формуле
A = F S = F S cos(F S ).
7
Задание 1
По координатам точек A, B и C для указанных векторов найти: а) модуль вектора a ;
б) скалярное произведение векторов a и b ; в) проекцию вектора c на вектор d ;
г) координаты точки M, делящей отрезок l в отношении α:β; д) угол между векторами a и b ;
е) направляющие косинусы вектора d .
1.1. A(4, 6, 3), B(– 5, 2, 6), C(4, – 4, – 3),
a = 4 CB – AC , b = AB , c = CB , d = AC , l = AB, α = 5, β = 4.
1.2. A(4, 3, – 2), B(– 3, – 1, 4), C(2, 2, 1),
a = – 5 AC + 2 CB , b = AB , c = AC , d = CB , l = BC, α = 2, β = 3.
1.3. A(– 2, – 2, 4), B(1, 3, – 2), C(1, 4, 2),
a = 2 AC – 3 BA, b = BC , c = BC , d = AC , l = BA, α = 2, β = 1.
1.4. A(2, 4, 3), B(3, 1, – 4), C(– 1, 2, 2),
a = 2 BA + 4 AC , b = BA, c = b , d = AC , l = BA, α = 1, β = 4.
1.5. A(2, 4, 5), B(1, – 2, 3), C(– 1, – 2, 4),
a = 3 AB – 4 AC , b = BC , c = b , d l = AB, α = 2, β = 3.
1.6. A(– 1, – 2, 4), B(– 1, 3, 5), C(1, 4, 2),
a = 3 AC – 7 BC , b = AB , c = b , d l = AC, α = 1, β = 7.
1.7. A(1, 3, 2), B(– 2, 4, – 1), C(1, 3, – 2),
 + 5 CB , b = AC , c = b , d l = AB, α = 2, β = 4.
+ 5 CB , b = AC , c = b , d l = AB, α = 2, β = 4.
1.8. A(2, – 4, 3), B(– 3, – 2, 4), C(0, 0, – 2),
 – 4 CB , b = c = AB , d = CB , l = AC, α = 2, β = 1.
– 4 CB , b = c = AB , d = CB , l = AC, α = 2, β = 1.
1.9. A(3, 4, – 4), B(– 2, 1, 2), C(2, – 3, 1),
 + 4 AC , b = c = BA, d = AC , l = BA, α = 2, β = 5.
+ 4 AC , b = c = BA, d = AC , l = BA, α = 2, β = 5.
1.10. A(0, 2, 5), B(2, – 3, 4), C(3, 2, – 5),
 + 4 CB , b = c = AC , d = AB , l = AC, α = 3, β = 2.
+ 4 CB , b = c = AC , d = AB , l = AC, α = 3, β = 2.
8

1.11. A(– 2, – 3, – 4), B(2, – 4, 0), C(1, 4, 5), a = 4 AC – 8 BC , b = c = AB , d = BC , l = AB, α = 4, β = 2.
1.12. A(– 2, – 3, – 2), B(1, 4, 2), C(1, – 3, 3), a = 2 AC – 4 BC , b = c = AB , d = AC , l = BC, α = 3, β = 1.
1.13. A(5, 6, 1), B(– 2, 4, – 1), C(3, – 3, 3), a = 3 AB – 4 BC , b = c = AC , d = AB , l = BC, α = 3, β = 2.
1.14. A(10, 6, 3), B(– 2, 4, 5), C(3, – 4, – 6), a = 5 AC – 2 CB , b = c = BA, d = AC , l = CB, α = 1, β = 5.
1.15. A(3, 2, 4), B(– 2, 1, 3), C(2, – 2, – 1),
a = 4 BC – 3 AC , b = BA, c = AC , d = BC , l = AC, α = 2, β = 4.
1.16. A(– 2, 3, – 4), B(3, – 1, 2), C(4, 2, 4), a = 7 AC + 4 CB , b = c = AB , d = CB , l = AB, α = 2, β = 5.
1.17. A(4, 5, 3), B(– 4, 2, 3), C(5, – 6, – 2),
 – 4 BC , b = c = AC , d = AB , l = BC, α = 5, β = 1.
– 4 BC , b = c = AC , d = AB , l = BC, α = 5, β = 1.
1.18. A(2, 4, 6), B(– 3, 5, 1), C(4, – 5, – 4),
 + 2 BA, b = c = CA, d = BA, l = BC, α = 1, β = 3.
+ 2 BA, b = c = CA, d = BA, l = BC, α = 1, β = 3.
1.19. A(– 4, – 2, – 5), B(3, 7, 2), C(4, 6, – 3), a = 9 BA + 3 BC , b = c = AC , d = BC , l = BA, α = 4, β = 3.
1.20. A(5, 4, 4), B(– 5, 2, 3), C(4, 2, – 5),
 – 6 AB , b = BC , c = AB , d = AC , l = BC, α = 3, β = 1.
– 6 AB , b = BC , c = AB , d = AC , l = BC, α = 3, β = 1.
1.21. A(3, 4, 6), B(– 4, 6, 4), C(5, – 2, – 3),
 + 4 CA, b = BA, c = CA, d = BC , l = BA, α = 5, β = 3.
+ 4 CA, b = BA, c = CA, d = BC , l = BA, α = 5, β = 3.
1.22. A(– 5, – 2, – 6), B(3, 4, 5), C(2, – 5, 4), a = 8 AC – 5 BC , b = c = AB , d = BC , l = AC, α = 3, β = 4.
1.23. A(3, 4, 1), B(5, – 2, 6), C(4, 2, – 7),
 + 5 AB , b = c = BC , d = AC ,
+ 5 AB , b = c = BC , d = AC ,
9
l = AB, α = 2, β = 3.
1.24. A(4, 3, 2), B(– 4, – 3, 5), C(6, 4, – 3), a = 8 AC – 5 BC , b = c = BA, d = AC , l = BC, α = 2, β = 5.
1.25. A(– 5, 4, 3), B(4, 5, 2), C(2, 7, – 4),
a = 3 BC + 2 AB , b = c = CA, d = AB , l = BC, α = 3, β = 4.
1.26. A(6, 4, 5), B(– 7, 1, 8), C(2, – 2, – 7),
a = 5 CB – 2 AC , b = AB , c = CB , d = AC , l = AB, α = 3, β = 2.
1.27. A(6, 5, – 4), B(– 5, – 2, 2), C(3, 3, 2), a = 6 AB – 3 CB , b = c = AC , d = CB , l = BC, α = 1, β = 5.
1.28. A(– 3, – 5, 6), B(3, 5, – 4), C(2, 6, 4),
a = 4 AC – 5 BA, b = CB , c = BA, d = AC , l = BA, α = 4, β = 2.
1.29. A(3, 5, 4), B(4, 2, – 3), C(– 2, 4, 7),
a = 3 BA – 4 AC , b = AB , c = BA, d = AC , l = BA, α = 2, β = 5.
1.30. A(4, 6, 7), B(2, – 4, 1), C(– 3, – 4, 2), a = 5 AB – 2 AC , b = c = BC , d = AB , l = AB, α = 3, β = 4.
Пример решения задания 1
По координатам точек A(– 5, 1, 6), B(1, 4, 3) и C(6, 3, 9) найти: а) модуль вектора a = 4 AB + BC ;
б) скалярное произведение векторов a и b = BC ;
в) проекцию вектора c = b на вектор d = AB ;
г) координаты точки M, делящей отрезок l = AB в отношении 1:3; д) угол между векторами a и b ;
е) направляющие косинусы d .
►а) Последовательно находим AB = (6, 3, – 3), BC
|
4AB + BC |
|
= 292 + 112 + (− 6)2 = 998 ; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
б) Имеем: a = (29, 11, – 6), |
|
|
|
= (5, – 1, 6). Тогда |
||||||||||||
|
b |
||||||||||||||||
|
|
|
a · |
|
=29·5 + 11·(– 1) + (– 6)·6 = 98; |
||||||||||||
|
|
|
b |
||||||||||||||
|
в) Так как |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
прd c |
= |
c |
|
d |
, |
|
|
= (6, 3, – 3), |
||||||
|
|
|
|
|
|
|
|
|
d |
||||||||
|
|
|
|
d |
|
|
|||||||||||
+ BC = (29, 11, – 6),
10
