2638 ЭИ

c ·

= 30 – 3 – 18 = 9,

|

d

| = 36+ 9 + 9 = 54 ,

то

d

9

прAB BC =

;

rA +

rB

54

г) Имеем: λ =

1

,

rM

=

. Следовательно,

1 + λ

3

− 5 +

1

1

7

1 + 4 1

7

xM =

3

= −

,

yM =

3

=

,

1

1

1 +

4

1 +

2

3

3

6 + 1

3

1

21

7

7

21

zM

=

=

, M

−

,

,

;

1 + 13

4

2

4

4

a =

д) Имеем: a = (29, 11, – 6),

= (5, – 1, 6),

998 , a

= 98. Тогда

b

b

98

cos(a ^ b )=

a b

98

=

998

52 + (− 1)2 + 62 =

998

62 = 0,394,

a

b

(a^

)= arccos 0,394;

b

е) Имеем:

= (6, 3, – 3),

d

=

54 . Тогда

d

dx

6

d y

3

dz

3

cosα =

d

=

54 , cos β = d

=

54

, cosγ =

d

= −

54 .

Делаем проверку: cos2 α + cos2 β + cos2 γ = 1 , 3654 + 549 + 549 = 1 .◄

6. Векторноепроизведениевекторовиегоприложения

Упорядоченная тройка некомпланарных векторов a , b , c с общим началом в точке O называется правой, если кратчайший поворот от вектора a к вектору b , наблюдаемый из конца вектора c , происходит против движения часовой стрелки. В противном случае тройка называется левой.

c

c

a

b

a

b

Векторным произведением векторов a и

называется вектор c , обозначаемый

b

c = a ×

, который удовлетворяет следующим трем условиям:

b

1)

c

=

a

sin(a bv);

b

2)

c a , c

;

b

3) тройка a , b , c – правая.

Основные свойства векторного произведения векторов:

11

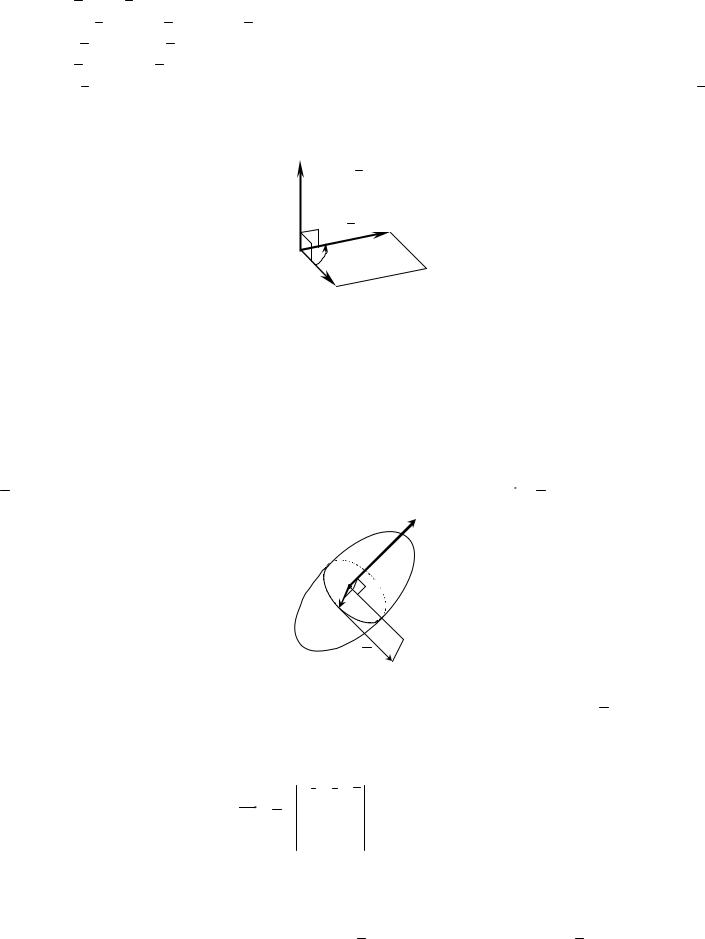
1) a × b = – ( b × a );

2)(λa )× b = λ( a × b ) = a × (λb );

3)a × ( b + c ) = a × b + a × c ;

4)a × b = 0 a || b ;

5)| a × b | = S, где S – площадь параллелограмма, построенного на векторах a и b ,

имеющих общее начало в точке O.

	c = a × b
	b
0	S
	a

Если a = (x1, y1, z1),

= (x2, y2, z2), то векторное произведение a ×

выражается через

b

b

координаты данных векторов a и

следующим образом:

b

i

j

k

y

z

1

x

z

1

x

y

1

a × b =

x1

y1

z1

1

,

−

1

,

1

.

=

y2

z2

x2

z2

x2

y2

x2

y2

z2

С помощью векторного произведения можно вычислить вращающий момент M силы F , приложенной к точке B тела, закрепленного в точке A: M = BA × F .

M

A

B

F

Пример. Вычислить координаты вращающего момента M силы F = (3, 2, 1), приложенной к точке A(– 1, 2, 4), относительно начала координат O.

►Имеем

i j k

M = OA × F = − 1 2 4 = (– 6, 13, – 8).◄

3 2 1

7. Смешанноепроизведение векторовиегоприложения

Смешанным произведением векторов a , b , c называется число ( a × b )· c . Основные свойства смешанного произведения векторов:

12

1) ( a × b )· c = a ·( b × c ), поэтому смешанное произведение можно обозначить проще:

a b c ;

2) a

c =

c a = c a

= –

a c = – c

a = – a c

;

b

b

b

b

b

b

3) a

c

= 0 a ,

, c

компланарны.

b

b

Если a

= (x1, y1, z1),

= (x2, y2, z2), c = (x3, y3, z3), то

b

			x1	y1	z1
a		c =	x2	y2	z2	.
	b
			x3	y3	z3

4) геометрический смысл смешанного произведения заключается в следующем: a b c = ± V, где V – объем параллелепипеда, построенного на перемножаемых векторах, взятый со знаком «+», если тройка векторов a , b , c – правая, или со знаком «–», если она левая;

+V	–V
c	c
b	a
0	0
a	b

Объем Vпар параллелепипеда, построенного на векторах a , b и c , и объем Vпир

образованной ими треугольной пирамиды

находятся по формулам

Vпар =

a

c

,

Vпир =

1

a

c

.

b

b

6

Задание 2

2.1. Даны векторы a , b и c . Необходимо:

а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов;

г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.

2.1.1. a = 2 i – 3 j + k , b = j + 4 k , c = 5 i + 2 j – 3 k ;

а) a , 3 b , c ; б) 3 a , 2 c ; в) b , – 4 c ; г) a , c ; д) a , 2 b , c . 2.1.2. a = 3 i + 4 j + k , b = i – 2 j + 7 k , c = 3i – 6 j + 21 k ;

а) 5 a , 2 b , c ; б) 4 b , 2 c ; в) a , c ; г) b , c ; д) 2 a , – 3 b , c . 2.1.3. a = 2 i – 4 j – 2 k , b = 7 i + 3 j , c = 3 i + 5 j – 7 k ;

а) a , 2b , 3c ; б) 3a , – 7b ; в), c , – 2a ; г) a , c ; д) 3a , 2b , 3c .

13

2.1.4. a = – 7 i + 2 k , b = 2 i – 6 j + 4 k , c = i – 3 j + 2 k ;

а) a , – 2 b , – 7 c ; б) 4 b , 3 c ; в) 2 a , – 7 c ; г) b , c ; д) 2 a , 4 b , 3 c . 2.1.5. a = – 4 i + 2 j – k , b = 3i + 5 j – 2 k , c = j + 5 k ;

а) a , 6 b , 3 c ; б) 2 b , a ; в) a , – 4 c ; г) a , b ; д) a , 6 b , 3 c . 2.1.6. a = 3 i – 2 j + k , b = 2 j – k , c = – 3 i + 2 j – k ;

а) a , – 3 b , 2 c ; б) 5 a , 3 c ; в) – 2 a , 4 b ; г) a , c ; д) 5 a , 4 b , 3 c . 2.1.7. a = 4 i – j + 3 k , b = 2i + 3 j – 5 k , c = 7i + 2 j + 4 k ;

а) 7 a , – 4 b , 2 c ; б) 3 a , 5 c ; в) 2 b , 4 c ; г) b , c ; д) 7 a , 2 b , 5 c . 2.1.8. a = 4 i + 2 j – 3 k , b = 2i + k , c = – 12i – 6 j + 9 k ;

а) 2 a , 3b , c ; б) 4a , 3b ; в) b , – 4c ; г) a , c ; д) 2 a , 3b , – 4c . 2.1.9. a = – i + 5 k , b = – 3i + 2 j + 2 k , c = – 2 i – 4 j + k ;

а) 3 a , – 4 b , 2 c ; б) 7 a , – 3 c ; в) 2 b , 3 a ; г) b , c ; д) 7 a , 2 b , – 3 c .

2.1.10. a

=

6i –

4

+ 6

,

= 9 i – 6

+ 9

, c = i – 8

;

k

k

k

b

j

j

а) 2 a , – 4

, 3

; б) 3

, – 9

; в) 3 a , – 5 c ; г) a ,

; д) 3 a , – 4

, – 9 c .

b

c

b

c

b

b

2.1.11. a

=

5i –

3

+ 4

,

= 2 i – 4

– 2

, c = 3 i + 5

– 7

;

k

k

k

b

j

j

j

а) a , –4

, 2 c ; б) – 2

, 4 c ; в) – 3 a , 6 c ; г)

, c ; д) a , –– 2

, 6 c .

b

b

b

b

2.1.12. a

= – 4i

+ 3

– 7

,

= 4 i + 6

– 2

, c = 6 i + 9

– 3

;

k

k

k

b

j

j

j

а) – 2 a ,

, – 2 c ; б) 4

, 7 c ; в) 5 a , – 3

; г)

, c ; д) – 2 a , 4

, 7

.

b

b

b

b

b

c

2.1.13. a

= – 5i

+ 2

– 2

,

= 7 i – 5

, c = 2 i + 3

– 2

;

k

k

k

b

j

j

а) 2 a , 4

, – 5 c ; б) – 3

, 11 c ; в) 8 a , – 6 c ; г) a , c ; д) 8 a , – 3

, 11 c .

b

b

b

2.1.14. a

= – 4i

– 6

+ 2

,

= 2 i + 3

–

, c = – i + 5

– 3

;

k

k

k

b

j

j

j

а) 5 a , 7

, 2 c ; б) – 4

, 11 a ; в) 3 a , – 7 c ; г) a ,

; д) 3 a , 7

, – 2 c .

b

b

b

b

2.1.15. a

= – 4i

+ 2

– 3

,

= – 3

+ 5

, c = 6 i + 6

– 4

;

k

k

k

b

j

j

j

а) 5 a , –

, 3 c ; б) – 7 a , 4 c ; в) 3 a , 9

; г) a , c ; д) 3 a , – 9

, 4 c .

b

b

b

2.1.16. a

= – 3i

+ 8

,

= 2i + 3

– 2

, c = 8 i + 12

– 8

;

b

k

k

j

j

j

а) 4 a , – 6

, 5 c ; б) – 7 a , 9 c ; в) 3

, – 8 c ; г)

, c ; д) 4 a , – 6

, 9 c .

b

b

b

b

2.1.17. a

= 2i –

4

– 2

,

= – 9 i + 2

, c = 3 i + 5

– 7

;

k

k

k

b

j

j

а) 7 a , 5

, – c ; б) – 5 a , 4

; в) 3

, – 8 c ; г) a , c ; д) 7 a , 5

, – c .

b

b

b

b

2.1.18. a

= 9i –

3

+

,

= 3i – 15

+ 21

, c = i – 5

+ 7

;

k

k

k

b

j

j

j

а) 2 a , – 7

, 3 c ; б) – 6 a , 4 c ; в) 5

, 7 a ; г)

, c ; д) 2 a , – 7

, 4 c .

b

b

b

b

2.1.19. a

= – 2i

+ 4

– 3

,

= 5 i +

– 2

, c = 7 i + 4

–

;

k

k

k

b

j

j

j

а) a , – 6

, 2 c ; б) – 8

, 5 c ; в) – 9 a , 7 c ; г) a ,

; д) a , – 6

, 5 c .

b

b

b

b

2.1.20. a = – 9i

+ 4

– 5

,

= i – 2

+ 4

, c = – 5i + 10

– 20

;

k

k

k

b

j

j

j

а) – 2 a , 7

, 5 c ; б) – 6

, 7 c ; в) 9 a , 4 c ; г)

, c ; д) – 2 a , 7

, 4 c .

b

b

b

b

2.1.21. a

= 2i –

7

+ 5

,

= – i + 2

– 6

, c = 3 i + 2

– 4

;

k

k

k

b

j

j

j

а) – 3 a , 6

, – c ; б) 5

, 3 c ; в) 7 a , – 4

; г)

, c ; д) 7 a , – 4

, 3 c .

b

b

b

b

b

2.1.22. a

= 7i –

4

– 5

,

= i – 11

+ 3

, c = 5 i + 5

+ 3

;

k

k

k

b

j

j

j

а) 3 a , – 7b , 2 c ; б) 2b , 6 c ; в) – 4 a , – 5 c ; г) a , c ; д) – 4 a , 2 b , 6 c .

14

2.1.23. a

= 4i

– 6

– 2

,

= – 2 i + 3

+

, c = 3i – 5

+ 7

;

k

k

k

b

j

j

j

а) 6 a , 3

, 8 c ; б) – 7

, 6 a ; в) – 5 a , 4 c ; г) a ,

; д) – 5 a , 3

, 4 c .

b

b

b

b

2.1.24. a

= 3i

–

+ 2

,

= – i + 5

– 4

, c = 6 i – 2

+ 4

;

k

k

k

b

j

j

j

а) 4 a , – 7

, – 2 c ; б) 6 a , – 4 c ; в) – 2 a , 5

; г) a , c ; д) 6 a , – 7

, – 2 c .

b

b

b

2.1.25. a

= – 3i –

– 5

,

= 2 i – 4

+ 8

, c = 3 i + 7

–

;

k

k

k

b

j

j

j

а) 2 a , –

, 3 c ; б) – 9 a , 4 c ; в) 5

, – 6 c ; г)

, c ; д) 2 a , 5

, – 6 c .

b

b

b

b

2.1.26. a

= – 3i + 2

+ 7

,

= i – 5

, c = 6i + 4

–

;

k

k

k

b

j

j

а) – 2 a ,

, 7 c ; б) 5 a , – 2 c ; в) 3

, c ; г) a , c ; д) – 2 a , 3

, 7 c .

b

b

b

2.1.27. a

= 3i

–

+ 5

,

= 2i – 4

+ 6

, c = i – 2

+ 3

;

k

k

k

b

j

j

j

а) – 3 a , 4

, 5 c ; б) 6

, 3 c ; в) a , 4 c ; г)

, c ; д) – 3 a , 4

, – 5 c .

b

b

b

b

2.1.28. a

= 4i

+ 5

– 4

,

= 5 i –

, c = 2i + 4

– 3

;

k

k

b

j

j

j

а) a , 7

, – 2 c ; б) – 5 a , 4

; в) 8 c , – 3 a ; г) a , c ; д) – 3 a , 4

, 8 c .

b

b

b

2.1.29. a

= – 9i + 4

,

= 2i – 4

+ 6

, c = 3 i – 6

+ 9

;

k

k

k

b

j

j

а) 3 a , – 5

, – 4 c ; б) 6

, 2 c ; в) – 2 a , 8 c ; г)

, c ; д) 3 a , 6

, .– 4 c .

b

b

b

b

2.1.30. a

= 5i

– 6

– 4

,

= 4 i + 8

– 7

, c = 3

– 4

;

k

k

k

b

j

j

j

а) 5 a , 3 b , – 4 c ; б) 4 b , a ; в) 7 a – 2 c ; г) a , b ; д) 5 a , 4 b , – 2 c .

2.2. Вершины пирамиды находится в точках A, B, C и D. Вычислить: а) площадь указанной грани;

б) площадь сечения, проходящего через середину ребра l и две вершины пирамиды; в) объем пирамиды ABCD.

2.2.1.A( 3, 4, 5), B(1 , 2, 1), C(– 2, – 3, 6), D(3, – 6, – 3);

а) ACD; б) l = AB, C и D.

2.2.2.A(– 7, – 5, 6), B(– 2, 5, – 3), C(3, – 2, 4), D(1, 2, 2);

а) BCD; б) l = CD, A и B.

2.2.3.A(1, 3, 1), B(– 1, 4, 6), C(– 2, – 3, 4), D(3, 4, – 4);

а) ACD; б) l = BC, A и D.

2.2.4.A(2, 4, 1), B(– 3, – 2, 4), C(3, 5, –2), D(4, 2, – 3);

а) ABD; б) l = AC, B и D.

2.2.5.A(– 5, – 3, – 4), B(1, 4, 6), C(3, 2, – 2), D(8, – 2, 4);

а) ACD; б) l = BC, A и D.

2.2.6.A(3, 4, 2), B(– 2, 3, – 5), C(4, – 3, 6), D(6, – 5, 3);

а) ABD; б) l = BD, A и C.

2.2.7.A(– 4, 6, 3), B(3, – 5, 1), C(2, 6, – 4), D(2, 4, – 5);

а) ACD; б) l = AD, B и C.

2.2.8.A(7, 5, 8), B(– 4, –5, 3), C(2, –3, 5), D(5, 1, – 4);

а) BCD; б) l = BC, A и D.

2.2.9.A(3, – 2, 6), B(– 6, – 2, 3), C(1, 1, – 4), D(4, 6, – 7);

а) ABD; б) l = BD, A и C.

15

2.2.10.A(– 5, – 4, – 3), B(7, 3, – 1), C(6, – 2, 0), D(3, 2, – 7);

а) BCD; б) l = AD, B и C.

2.2.11.A(3, – 5, – 2), B(– 4, 2, 3), C(1, 5, 7), D(– 2, – 4, 5);

а) ACD; б) l = BD, A и C.

2.2.12.A(7, 4, 9), B(1, – 2, – 3), C(– 5, – 3, 0), D(1, – 3, 4);

а) ABD; б) l = AB, C и D.

2.2.13.A(– 4, – 7, – 3), B(– 4, – 5, 7), C(2, – 3, 3), D(3, 2, 1);

а) BCD; б) l = BC, A и D.

2.2.14.A(– 4, – 5, – 3), B(3, 1, 2), C(5, 7, – 6), D(6, – 1, 5);

а) ACD; б) l = BC, A и D.

2.2.15.A(5, 2, 4), B(– 3, 5, – 7), C(1, – 5, 8), D(9, – 3, 5);

а) ABD; б) l = BD, A и C.

2.2.16.A(– 6, 4, 5), B(5, – 7, 3), C(4, 2, – 8), D(2, 8, – 3);

а) ACD; б) l = AD, B и C.

2.2.17.A(5, 3, 6), B(– 3, – 4, 4), C(5, – 6, 8), D(4, 0, – 3);

а) BCD; б) l = BC, A и D.

2.2.18.A(5, – 4, 4), B(– 4, – 6, 5), C(3, 2, – 7), D(6, 2, – 9);

а) ABD; б) l = BD, A и C.

2.2.19.A(– 7, – 6, – 5), B(5, 1, – 3), C(8, – 4, 0), D(3, 4, – 7);

а) BCD; б) l = AD, B и C.

2.2.20.A(7, – 1, – 2), B(1, 7, 8), C(3, 7, 9), D(– 3, – 5, 2);

а) ACD; б) l = BD, A и C.

2.2.21.A(5, 2, 7), B(7, – 6, – 9), C(– 7, – 6, 3), D(1, – 5, 2);

а) ABD; б) l = AB, C и D.

2.2.22.A(– 2, – 5, – 1), B(– 6, – 7, 9), C(4, – 5, 1), D(2, 1, 4);

а) BCD; б) l = BC, A и D.

2.2.23.A(– 6, – 3, – 5), B(5, 1, 7), C(3, 5, – 1), D(4, – 2, 9);

а) ACD; б) l = BC, A и D.

2.2.24.A(7, 4, 2), B(– 5, 3, – 9), C(1, – 5, 3), D(7, – 9, 1);

а) ABD; б) l = BD, A и C.

2.2.25.A(– 8, 2, 7), B(3, – 5, 9), C(2, 4, – 6), D(4, 6, – 5);

а) ACD; б) l = AD, B и C.

2.2.26.A(4, 3, 1), B(2, 7, 5), C(– 4, – 2, 4), D(2, – 3, – 5);

а) ACD; б) l = AB, C и D.

2.2.27.A(– 9, – 7, 4), B(– 4, 3, – 1), C(5, – 4, 2), D(3, 4, 4);

а) BCD; б) l = CD, A и B.

2.2.28.A(3, 5, 3), B(– 3, 2, 8), C(– 3, – 2, 6), D(7, 8, – 2);

а) ACD; б) l = BD, A и C.

16

2.2.29.A(4, 2, 3), B(– 5, – 4, 2), C(5, 7, – 4), D(6, 4, – 7);

а) ABD; б) l = AD, B и C.

2.2.30.A(– 4, – 2, – 3), B(2, 5, 7), C(6, 3, – 1), D(6, – 4, 1);

а) ACD; б) l = BC, A и D.

2.3. Сила F приложена к точке A. Вычислить:

а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку B;

б)модуль момента силы F относительно точки B.

2.3.1.F = (5, – 3, 9), A(3, 4, – 6), B(2, 6, 5).

2.3.2.F = (– 3, 1, – 9), A(6, – 3, 5), B(9, 5, – 7).

2.3.3.F = (2, 19, – 4), A(5, 3, 4), B(6, – 4, – 1).

2.3.4.F = (– 4, 5, – 7), A(4, – 2, 3), B(7, 0, – 3).

2.3.5.F = (4, 11, – 6), A(3, 5, 1), B(4, – 2, – 3).

2.3.6.F = (3, – 5, 7), A(2, 3, – 5), B(0, 4, 3).

2.3.7.F = (5, 4, 11), A(6, 1, – 5), B(4, 2, – 6).

2.3.8.F = (– 9, 5, 7), A(1, 6, – 3), B(4, – 3, 5).

2.3.9.F = (6, 5, – 7), A(7, – 6, 4), B(4, 9, – 6).

2.3.10.F = (– 5, 4, 4), A(3, 7, – 5), B(2, – 4, 1).

2.3.11.F = (4, 7, – 3), A(5, – 4, 2), B(8, 5, – 4).

2.3.12.F = (2, 2, 9), A(4, 2, – 3), B(2, 4, 0).

Даны три силы P, Q, R, приложенные к точке A. Вычислить: а) работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку B;

б)величину момента равнодействующей этих сил относительно точки B.

2.3.13.P = (9, – 3, 4), Q = (5, 6, – 2), R = (– 4, – 2, 7), A(– 5, 4, – 2), B(4, 6, – 5).

2.3.14.P = (5, – 2, 3), Q = (4, 5, – 3), R = (– 1, – 3, 6), A(7, 1, – 5), B(2, – 3, – 6).

2.3.15.P = (3, – 5, 4), Q = (5, 6, – 3), R = (– 7, – 1, 8), A(– 3, 5, 9), B(5, 6, – 3).

2.3.16.P = (– 10, 6, 5), Q = (4, – 9, 7), R = (5, 3, – 3), A(4, – 5, 9), B(4, 7, – 5).

2.3.17.P = (5, – 3, 1), Q = (4, 2, – 6), R = (– 5, – 3, 7), A(– 5, 3, 7), B(3, 8, – 5).

2.3.18.P = (– 5, 8, 4), Q = (6, – 7, 3), R = (3, 1, – 5), A(2, – 4, 7), B(0, 7, 4).

17

2.3.19.P = (7, 5, – 2), Q = (3, 4, – 8), R = (– 2, – 4, 3), A(– 3, 2, 0), B(6, 4, – 3).

2.3.20.P = (3, – 4, 2), Q = (2, 3, – 5), R = (– 3, – 2, 4), A(5, 3, – 7), B(4, – 1, – 4).

2.3.21.P = (4, – 2, – 5), Q = (5, 1, – 3), R = (– 6, 2, 5), A(– 3, 2, – 6), B(4, 5, – 3).

2.3.22.P = (7, 3, – 4), Q = (9, – 4, 2), R = (– 6, 1, 4), A(– 7, 2, 5), B(4, – 2, 11).

2.3.23.P = (9, – 4, 4), Q = (– 4, 6, – 3), R = (3, 4, 2), A(5, – 4, 3), B(4, – 5, 9).

2.3.24.P = (6, – 4, 5), Q = (– 4, 7, 8), R = (5, 1, – 3), A(– 5, – 4, 2), B(7, – 3, 6).

2.3.25.P = (5, 5, – 6), Q = (7, – 6, 6), R = (– 4, 3, 4), A(– 9, 4, 7), B(8, – 1, 7).

2.3.26.P = (7, – 6, 2), Q = (– 6, 2, – 1), R = (1, 6, 4), A(3, – 6, 1), B(6, – 2, 7).

2.3.27.P = (4, – 2, 3), Q = (– 2, 5, 6), R = (7, 3, – 1), A(– 3, – 2, 5), B(9, – 5, 4).

2.3.28.P = (7, 3, – 4), Q = (3, – 2, 2), R = (– 5, 4, 3), A(– 5, 0, 4), B(4, – 3, 5).

2.3.29.P = (3, – 2, 4), Q = (– 4, 4, – 3), R = (3, 4, 2), A(1, – 4, 3), B(4, 0, – 2).

2.3.30.P = (2, – 1, – 3), Q = (3, 2, – 1), R = (– 4, 1, 3), A(– 1, 4, – 2), B(2, 3, – 1).

Пример решения задания 2

2.1. Даны векторы

a = 4 i + 4 k , b = – i + 3 j + 2 k , c = 3 i + 5 j .

Необходимо:

а) вычислить смешанное произведение векторов a , b и 5 c ; б) найти модуль векторного произведения 3 c и b ;

в) вычислить скалярное произведение векторов a и 3b ;

г) проверить, будут ли коллинеарны или ортогональны векторы a и b ; д) проверить, будут ли компланарны векторы a , b и c .

► а) Так как 5 c = 15i + 25 j , то

			4	0	4
(a ×		) 5c =	− 1	3	2	= – 100 – 180 – 200 = – 480;
	b
			15	25	0

18

19

б) Поскольку 3 c = 9i

+ 15

j

, то

i

j

k

3c ×

=

9 15

0

b

= 30i

+ 27 k + 15 k – 18

j

= 30i – 18

j

+ 42 k .

− 1

3

2

в) Находим:

3

= – 3 i + 9

+ 6

, a ·3

= 4·(– 3) + 0·9 + 4·6 = 12;

b

k

b

j

г) Так как

a

= (4, 0, 4),

= (– 1, 3, 2) и

4

≠

0

≠

4

,

b

− 1

2

3

то векторы a и b не коллинеарны. Поскольку

a · b = 4·(– 1) + 0·3 + 4·2 ≠ 0,

то векторы a и b не ортогональны;

д) Векторы a , b , c компланарны, если ab c = 0. Вычисляем:

			4	0	4
a		c =	−1 3		2	= – 20 – 36 – 40 ≠ 0,
	b
			3	5	0

т. е. векторы a , b , c не компланарны. ◄

2.2. Вершины пирамиды находится в точках

A(2, 3, 4), B(4, 7, 3), C(1, 2, 2) и D(– 2, 0, – 1).

Вычислить:

а) площадь грани ABC;

б) площадь сечения, проходящего через середину ребер AB, AC. AD; в) объем пирамиды ABCD.

► а) Известно, что SABC = 12 AB × AC . Находим:

AB = (2, 4, – 1), AC = (– 1, – 1, – 2),

k

i

j

AB × AC =

2 4 − 1

= − 9i

+ 5 j + 2k .

−1

−1

2

Окончательно имеем:

SABC = 1

92 + 52 + 22

=

1

110 ;

2

2

б) Середины ребер AB, AC и AD находятся в точках K(3; 5; 3,5), M(1,5; 2,5; 3), N(0; 1,5; 1,5). Далее имеем:

Sсеч = 12 KM × KN , KM = (– 1,5; – 2,5; – 0,5), KN = (– 3; – 3,5; – 2),

k

i

j

KM × KN =

− 1,5 − 2,5 − 0,5

= 3,25i

− 1,5 j − 2,25k ,

− 3

− 3,5

− 2

Sсеч =

1

3,252

+ 1,52 + 2,25

2 = 1 17,875 ;

2

2

в) Поскольку V

=

1

(AB × AC) AD

, AD = (– 4, – 3, –5),

пир

6

2

4

− 1

= 11,

(AB × AC) AD =

− 1

− 1

− 2

− 4

− 3

− 5

то V =

11

. ◄

6

2.3. Сила F = (2, 3, – 5) приложена к точке A(1, – 2, 2). Вычислить: а) работу силы F в случае, когда точка ее

приложения,

двигаясь

прямолинейно,

перемещается в точку B(1, 4, 0);

б)модуль момента силы F относительно точки B.

► а) Так как A = F·s, s = AB = (0, 6, – 2), то

F· AB = 2·0 + 3·6 + (– 5)·(– 2) = 28;

б) Момент силы M = BA ·F, BA = (0, – 6, 2),

i

j

k

BA ·F =

0 − 6

2

= 24i

+ 4 j + 12k .

2

3

− 5

Следовательно, |M| = 242 + 42 +122 = 4 46 . ◄

8. Понятие базиса

Если для системы n векторов ai

равенство

n

∑ λ i ai = 0

i=1

верно только в случае, когда λi = 0, то эта система называется линейно независимой. Если же данное равенство выполняется для λi, хотя бы одно из которых отлично от нуля, то система векторов ai называется линейно зависимой. Например, любые коллинеарные векторы, или три компланарных вектора, всегда линейно зависимые.

Три упорядоченных линейно независимых вектора e1 , e2 , e3 в пространстве называются базисом. Упорядоченная тройка некомпланарных векторов всегда образует

20