Авсиевич_КР

Эти методы и составили сущность так называемой классической теории автоматического управления. Определение передаточной функции связано с преобразование Лапласа и поэтому вначале приведем некоторые основные сведения из этого преобразования [1,2].

При использовании преобразования Лапласа некоторой функции времени x(t) ставится в однозначное соответствие функция X(p), где p - оператор Лапласа. Функция времени x(t) называется оригиналом, а функция X(p) ее изображением. Изображение и оригинал связаны соотношением

X ( p) x(t)e pt dt .

0

Приведем некоторые теоремы преобразования Лапласа, которые потребуются для выполнения курсовой работы..

1. Теорема линейности. Для любых действительных или комплексных величин

Af (t) Bg(t) AF ( p) BG( p) ,

где знак означает соответствие изображения оригиналу.

2. Теорема запаздывания. Для любого постоянного > 0

f(t ) e p F( p) .

3.Теорема дифференцирования оригинала.

	.
Если	f (t) F( p) , то f pF( p) f (0) .
Применив эту теорему к производным высших порядков, получим
			.
		f (n) (t) pn F( p) pn 1 f (0) pn 2	f (0) ... f (n 1) (0) .
При нулевых начальных условиях предыдущее выражение упрощается
		f n (t) pn F( p) .
			t
4. Теорема интегрирования оригинала. Если			f (t) F( p) и g(t) f (t)dt , то
			0
g(t)	F ( p)	.
	p

5. Теорема о начальном значении оригинала.

f (0) lim pF( p) .

p

6. Теорема о конечном значении оригинала.

f ( ) lim pF( p) .

p 0

Перейдем к определению передаточной функции. Пусть система или какое-либо звено ее описываются дифференциальным уравнением вида (1). Полагая начальные условия нулевыми, перейдем в этом уравнении к изображениям по Лапласу. В соответствии с теоремой 3 получим

a0 p n X ( p) a1 p n 1 X ( p) ... an 1 pX ( p) an X ( p) .b0 p mG( p) b1 p m 1G( p) ... bm 1 pG( p) bmG( p)

Вынесем в полученном выражении за скобки изображения переменной и входного воздействия и сделаем обозначения

A( p) a0 pn a1 pn 1 ... an 1 p an , B( p) b0 pm b1 pm 1 ... bm 1 p bm .

С учетом этих обозначений исходное дифференциальное уравнение в изображениях по Лапласу получит вид

11

A( p)X ( p) B( p)G( p) .

Определим теперь зависимость выходной величины от входного воздействия

X ( p)	B( p)	G( p) W ( p)G( p) .	(2)
	A( p)

Передаточной функцией системы (звена) W(p) называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.

Требование нулевых начальных условий не вносит принципиальных трудностей. В случае x(0)(k) 0, при переходе к изображениям используют теорему 3, переносят члены, соответствующие начальным условиям в правую часть уравнения и считают их возмущающими воздействиями, относительно которых получают передаточные функции.

Пример. Составление дифференциального уравнения по известной передаточной функции.

Пусть имеется следующая передаточная функция:

W ( p)		kp
			.
	T p 2	T p 1
2		1

Для записи дифференциального уравнения по заданной передаточной функции, перепишем еѐ в соответствии с определением

		W ( p)	X ( p)			kp		.
			G( p)		T p 2	T p 1
				2		1
Полученное		выражение	преобразуем					к	следующему	виду
X ( p)(T p2	T p 1) kpG( p) и раскроем скобки
2	1
		T p2 X ( p) T pX ( p) X ( p) kpG( p) .
		2	1

В полученном уравнении произведем замену оператора p dtd , что соответствует

обратному преобразованию Лапласа, и получим результирующее дифференциальное уравнение

T	d 2	x(t) T	d	x(t) x(t) k	d	g(t) .
	dt 2
2		1 dt			dt

Частотные характеристики САУ

В начале приведем понятия частотных функций и их определение. Пусть входное воздействие g(t) представляет собой гармоническую функцию вида

g(t) Gm cos(t) .

Используя формулу Эйлера, можно записать

	cos(t)	e j t e j t
			.
		2

Тогда входное воздействие можно представить в виде суммы двух воздействий

g(t) g1 (t) g2 (t) G2m e j t G2m e j t .

Дифференциальное уравнение системы в изображениях по Лапласу запишется в

виде

A( p)X ( p) B( p)G( p) ,

(3)

12

где полином A( p) имеет порядок n, а полином B( p) -порядок m.

Пусть на вход системы подано воздействие

вида g1 (t) . Частное

решение

дифференциального уравнения будем искать в виде

x (t)

Gm

W ( j)e j t ,

1

2

где W ( j) - некоторая функция частоты .

Подставив g1(t) и x1(t) в (3), сократив полученное выражение на Gm/2

и e-j t,

получим

(a

( j)n a ( j)n 1

... a

n

)W ( j) b ( j)m b ( j)m 1 b .

0

1

0

0

m

Отсюда следует

W ( j)

b ( j)m

b ( j)m 1

b

B( j)

0

0

m

.

(4)

a

( j)n a ( j)n 1 ... a

A( j)

0

1

n

Сравнивая выражения (4) и (2), можно заключить, что функция W(j ) получается из передаточной функции W(p) простой заменой p=j . Эта замена с математической точки зрения означает переход от преобразования Лапласа к преобразованию Фурье

[1,2].

Функция W(j ) называется частотной передаточной функцией системы. Комплексную функцию W(j ) представим в виде

W ( j) A( )e j ( ) .

(5)

Тогда

x (t)

Gm

A( )e j ( t ( )) .

1

2

Если в (3) подставить

функцию

g2 (t)

Gm

e j t , то

после преобразований,

2

аналогичных предыдущим, получим

x2 (t)

Gm

A( )e j ( t ( )) .

2

В соответствии с принципом суперпозиции

e j ( t ( )) e

j ( t ( ))

x(t) x (t) x

(t) G

m

A( )

G

m

A( ) cos(t ( )) .

1

2

2

Это выражение показывает, что вынужденные колебания, вызываемые в устойчивой линейной динамической системе гармоническим входным воздействием, представляют собой гармоническую функцию времени, имеющую ту же частоту, что и входное воздействие, но отличающуюся от последнего по амплитуде и по фазе.

Зависимость отношения А( ) амплитуды выходного сигнала к амплитуде входного сигнала от частоты называется амплитудной частотной характеристикой (АЧХ)

системы.

Зависимость фазового сдвига ( ) между входным и выходным сигналами от частоты называется фазовой частотной характеристикой (ФЧХ) системы.

С этой точки зрения частотную передаточную функцию W(j ) называют также

амплитудно-фазовой частотной характеристикой (АФЧХ) системы.

Методика определения частотных характеристик системы следующая.

1) В передаточной функции системы делают замену p=j и полученную АФЧХ представляют в виде суммы вещественной и мнимой частей.

	W ( p)|			B( j)	U ( ) jV ( ) ,
		p j		A( j)

13

где функцию U( ) называют вещественной частотной характеристикой, а функцию V( )- мнимой частотной характеристикой.

2) Определяют АЧХ и ФЧХ.

A( )

U 2 ( ) V 2 ( ) ,

( ) arctg

V ( )

.

U ( )

Пример. Определить частотные характеристики для звена с передаточной

функцией

W ( p)

k

.

Tp 1

Делаем замену p=j

W ( j)

k

k(1 jt)

k(1 jT)

.

jT

(1 jT)(1 jT)

1

1 T 2 2

Отсюда

U ( )

k

V ( ) k

T

;

;

1 T 2 2

1 T 2 2

A( )

k

;

( ) arctg (T) .

1 T 2 2

V( )

=

( ) A( )

( )

k

0

1/T

U( )

4

450

-450

A( )

900

W ( p)

k

Рис. 2. Частотные характеристики звена

.

Tp 1

Частотные характеристики широко используются при анализе и синтезе САУ и составляют основу рассматриваемой классической теории автоматического управления.

Логарифмические частотные характеристики САУ

Существенным недостатком рассмотренных выше частотных характеристик является то, что графически они, особенно для систем высокого порядка, являются кривыми достаточно сложной формы, что затрудняет их построение и использование для анализа систем. В целях исключения этого недостатка в большинстве случаев нашли применение логарифмические частотные характеристики (ЛЧХ).

Логарифмической амплитудной частотной характеристикой (ЛАХ) называется

кривая, соответствующая выражению

L( ) 20lg A( )

и построенная в логарифмическом масштабе частот.

14

Логарифмической фазовой частотной характеристикой (ЛФХ) называется фазовая частотная характеристика ( ), построенная в логарифмическом масштабе частот.

Величина L( ) измеряется в децибелах, а ( ) - в градусах или радианах. Единицами измерения логарифмической оси частот являются октавы и декады.

Октавой называется интервал частот, соответствующий изменению частоты в два раза и равный lg2=0,3010. Декадой называется интервал частот, соответствующий изменению частоты в десять раз и равный lg10=1. Легко подсчитать, что одна декада содержит 3,32 октавы. Точка, соответствующая значению частоты, равному нулю, лежит слева в бесконечности, т.к. lg0=- . Поэтому ось ординат проводится через любую точку оси частот так, чтобы справа располагалась та часть ЛЧХ, которую нужно исследовать.

Можно рекомендовать следующую методику построения логарифмической сетки координат. Вначале ось частот разбивается на декады и октавы, причем каждая декада разбивается на октавы отдельно. Для удобства инженерной практики под точками этой оси пишут не значения логарифмов частот, а сами частоты.

( ) L( ) -2700

декада	декада	декада
-1800
		lg
-900	октавы
0

Рис. 3. Оси логарифмической системы координат.

Рекомендуется ось ординат в отношении фазовой характеристики располагать так, чтобы с точкой начала координат совпадало значение фазы, равное -1800, положительное направление шло вниз, а отрицательное - вверх. Общепринятое расположение оси фазы не является ошибкой, но рекомендованное здесь расположение во многих случаях облегчает применение для анализа и синтеза систем разработанных графоаналитических методов.

Если исследуемая точка частоты не совпадает ни с октавой, ни с декадой, то ее положение на оси частот по отношению к началу координат или началу какой-либо декады при избранном масштабе m [мм/дек] можно определить по формуле

x m lg x .

0

Здесь 0 - частота, соответствующая началу координат или началу декады. Обратная задача, т.е. определение значения частоты по положению

соответствующей ей точки на оси частот, решается использованием формулы

x 010 x m .

При построениях ЛЧХ вручную удобным является масштаб равный m=50 мм/дек.

Во многих случаях передаточную функцию системы можно представить в виде произведения передаточных функций элементарных звеньев

n

W ( p) Wi ( p) .

i 1

15

n

Тогда W ( p) Wi ( p) Ai ( )e j i ( ) .

i 1

Всоответствии с правилами о логарифме произведения и произведении показательных функций получим

n	n
L( ) 20 lg Ai ( ) Li ( ) ,
i 1	i 1

( ) i ( ) .

i 1n

Таким образом, логарифмические характеристики сложной системы могут быть получены суммированием ЛЧХ составляющих ее простых звеньев.

Пример. Определить ЛЧХ для САУ с передаточной функцией

			W ( p)				k
								.
					Tp 1
Используя результаты предыдущего примера, получим
				k
		L( ) 20 lg					20 lg k 20 lg 1 T 2 2 .
				1 T 2 2
При	1	величина		T 2 2 1 и					L( ) 20lg k представляет собой уравнение
	T
прямой, параллельной оси частот.
При	1	величина		T 2 2			1		и L( ) 20lg k 20lg(T) является прямая,
	T

имеющая наклон к оси частот, равный -20 дБ/дек и сопрягающейся с предыдущей прямой в точке 0=1/T.

Таким образом, ЛАХ данной системы может быть приближенно построена в виде двух сопрягающихся отрезков прямых. Такая ЛАХ называется асимптотической. Возможность замены кривых асимптотическими ЛАХ является важным достоинством ЛЧХ. Ошибка при такой замене для большинства простых систем невелика и для рассматриваемой системы ее максимальное значение в точке = 0 не превышает 3 дБ.

( ) L( )

20lgk

-20дБ/дек

-1800 0	c
0=1/T	lg
-900

-450

Л ФХ

0

Рис. 4. ЛЧХ системы с передаточной функцией W ( p)	k
	Tp 1

16

Фазовая характеристика исследуемой системы определена выше.

Частота 0=1/T называется частотой сопряжения. Частота с, при которой ЛАХ пересекает ось частот, что соответствует значению А( )=1, называется частотой среза системы.

В заключение отметим, что так как для физически реализуемых систем n>m, то

lim W ( j) 0 .

Это означает, что все реально осуществимые системы являются фильтрами нижних частот.

Алгебраический критерий устойчивости Гурвица

Для оценки устойчивости по этому критерию необходимо из коэффициентов характеристического уравнения составить определитель Гурвица по следующим правилам:

1)по главной диагонали выписываются все коэффициенты характеристического уравнения от а1 до аn в порядке возрастания индексов;

2)столбцы определителя заполняются коэффициентами от главной диагонали вниз по убывающим, а вверх - по возрастающим индексам;

3)места коэффициентов, индексы которых больше n или меньше нуля заполняются

нулями.

Пример. Составим определитель Гурвица,

для системы 5-го порядка с

характеристическим уравнением системы

a

0

p5

a p4 a

2

p3

a

3

p2

a

4

p a

5

0 ,

1

где все коэффициенты строго больше нуля. Получим

a1

a3

a5

0

0

a0

a2

a4

0

0

n

0

a1

a3

a5

0

.

0

a0

a2

a4

0

0

0

a1

a3

a5

Для того чтобы все корни характеристического уравнения имели отрицательные вещественные части, и система была устойчивой необходимо и достаточно, чтобы все

17

коэффициенты и все диагональные определители определителя Гурвица были строго больше нуля.

Для устойчивости системы 5-го порядка необходимо выполнение условий аk>0, k=0,1,2,...5;

2 =а1а2 - а0а3>0;3=а3 2 - а12а4>0;

4 =а4 3 -а2а5 2 + а0а5(а1а4 - а0а5)>0;

5 =а5 4>0.

Так как при выполнении необходимого условия устойчивости всегда аn>0, то об устойчивости системы можно судить по определителям до n-1 включительно. Доказано,

что если n-1=0, то система находится на колебательной границе устойчивости, т.е. имеет пару чисто мнимых корней. Из условия n-1=0 можно определить критические значения параметров системы, при которых она выходит на границу устойчивости.

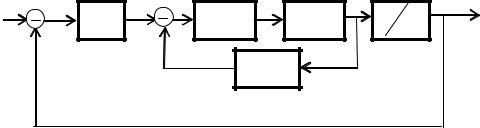
Пример. Исследовать устойчивость САУ. Система задана структурной схемой.

	*	Wрп ( p)			1
	k		W	( p)		p
			z
			k z

На схеме обозначено:

k - передаточное число (коэффициент передачи);

Wрп ( p)			1		;	W z ( p)	kc (T1 p 1)		;
	T	рп	p 1				T 2 p 2 2T p 1

k z - передаточное число обратной связи.

Для передаточной функции разомкнутой системы можно записать

Wp

( p)

k kcWрп ( p)W z ( p)

k kc (T1 p 1)

,

p(1 k

z

W

рп

( p)W

( p))

p(a

0

p3 a p2

a

2

p a

3

)

z

1

где a

0

T 2T

рп

;

a 2TT

T 2 ;

a

2

T

рп

2T k

z

k T ;

a

3

1 k

z

k

c

.

1

рп

c 1

Передаточная функция замкнутой системы примет вид

18

( p)

Wp ( p)

k k

c

(T p 1)

Wз

1

,

W

( p)

p(d

p3 d

p 2 d

p d

)

1

p

0

1

2

3

где d0 a0 ; d1 a1 ;

d2 a2 ; d3

a3 k kcT1 ; d4

k kc .

Составим определитель Гурвица

d1

d3

0

0

d0

d2

d 4

0

.

0

d1

d3

0

0

d0

d 2

d4

Оценим устойчивость системы для следующих значений параметров:

k

5 ; k z 1,2 ; kc 0,9 ; T1

1,8 ,

T 0,12 , Tрп 0,08 ;

0,1.

При этих значениях для коэффициентов характеристического уравнения получим

d0

a0 0,00115; d1

a1 0,0163 ;

d2

a2

2,048 ; a3

2 ; d3 10,18 ; d4

4,5 .

Следовательно, все коэффициенты характеристического уравнения замкнутой системы положительны и

2 d1d2 d0 d3 0,021675 0 ;

3 d3 2 d12 d4 0,21945 0 ;

4 d4 3 0,98755 0 .

Условия устойчивости выполнены и система при избранных параметрах устойчива.

Частотные критерии устойчивости

Принцип аргумента

Частотные критерии устойчивости используются в графоаналитическом виде и отличаются большой наглядностью при проведении расчетов. В основе всех частотных методов лежит принцип аргумента.

Рассмотрим характеристическое уравнение системы

D( p) d0 pn d1 pn 1 ... dn 1 p dn 0 .

Если i, i=1,2,...n- корни этого уравнения, то

D( p) d0 ( p 1 )( p 2 )...( p n ) .

Каждому корню на комплексной плоскости соответствует определенная точка, и

геометрически на этой плоскости каждый корень можно изобразить в виде вектора с

19

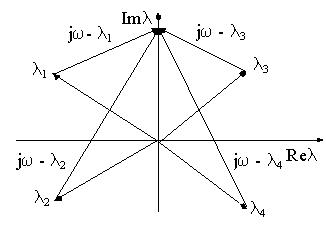
модулем i , проведенного из начала координат (рис.5.). Сделаем замену p=j и

получим

D( j) d0 ( j 1 )( j 2 )...( j n ) .

В соответствием с правилом вычитания векторов получим, что конец каждого элементарного вектора (j - i) находиться на мнимой оси.

Рис. 5. К определению принципа аргумента

Аргумент вектора D(j ) равен сумме аргументов элементарных векторов

n

arg D( j) arg( j i ) .

i 1

Направление вращения вектора (j - i) против часовой стрелки при изменении частоты от - до + принято считать положительным, а по часовой стрелке -

отрицательным. Предположим, что характеристическое уравнение имеет m корней в правой полуплоскости и (n – m) корней в левой полуплоскости. При изменении частоты от - до + каждый вектор (j - i), начало которого лежит в левой полуплоскости повернется на угол + , а каждый вектор, начало которого лежит в правой полуплоскости

- на угол - . Изменение аргумента вектора D(j ) при этом будет

arg D( j) (n m) m (n 2m) .	(6)

Это выражение и определяет принцип аргумента.

Изменение аргумента вектора D(j ) при изменении частоты от - до + равно

разности между числом (n-m) корней уравнения D(p)=0, лежащих в левой полуплоскости, и числом m корней этого уравнения, лежащих в правой полуплоскости, умноженной на .

20