Ekonometrika / Пример2

К примеру 2

Будем искать линейное уравнение регрессии в виде , где

Параметр называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если в функции издержек ( – издержки (тыс. руб.), – количество единиц продукции), то, следовательно, с увеличением объема продукции () на 1 ед. издержки производства возрастают в среднем на 2 тыс. руб., т. е. дополнительный прирост продукции на 1 ед. потребует увеличения затрат в среднем на 2 тыс. руб.

Формально – значение при . Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена не имеет смысла. Параметр может не иметь экономического содержания. Попытки экономически интерпретировать параметр могут привести к абсурду, особенно при .

Интерпретировать можно лишь знак при параметре . Если , то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация результата меньше вариации фактора – коэффициент вариации по фактору выше коэффициента вариации для результата

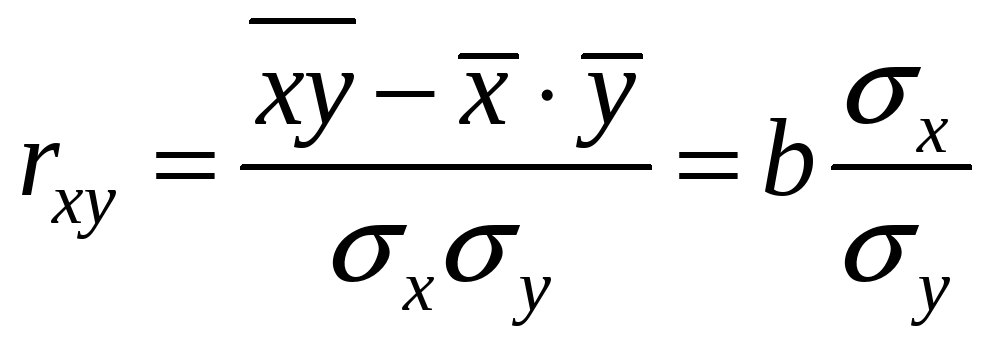
Как известно, линейный коэффициент корреляции находится в границах: .

Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака: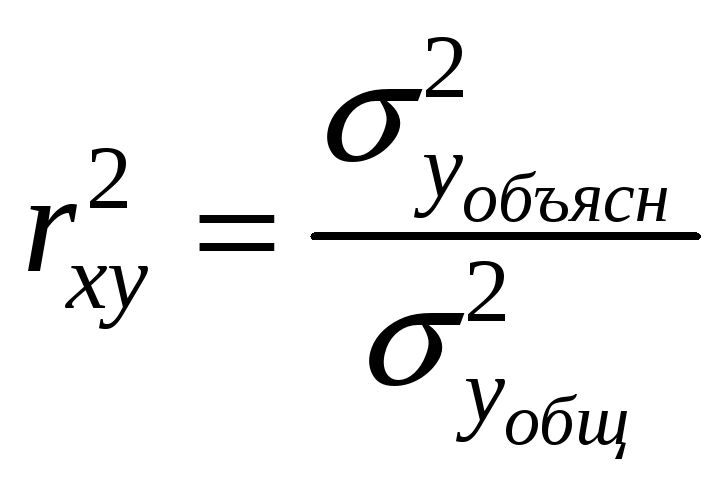

Соответственно величина характеризует долю дисперсии , вызванную влиянием остальных не учтенных в модели факторов.

Непосредственному расчету -критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной от среднего значения на две части – «объясненную» и «необъясненную»:

Любая сумма квадратов отклонений связана с числом степеней свободы (df– degrees of freedom), т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений от средней из возможных требуется для образования данной суммы квадратов. Так, для общей суммы квадратов независимых отклонений, ибо по совокупности из единиц после расчета среднего уровня свободно варьируют лишь число отклонений. Например, имеем ряд значений у: 1,2, 3, 4, 5. Среднее из них равно 3, и тогда отклонения от среднего составят: –2; –1; 0; 1; 2. Так как , то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если предыдущие четыре известны.

При расчете объясненной или факторной суммы квадратов используются теоретические (расчетные) значения результативного признака , найденные по уравнению линейной регрессии.

Величина определяется по уравнению линейной регрессии. Параметр можно найти как , тогда, подставив в линейную модель, получим:

.

Отсюда видно, что при заданном наборе переменных и расчетное значение является в линейной регрессии функцией только одного параметра – коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равное 1.

Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет . Число степеней свободы для общей суммы определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. .

Итак, имеем два равенства:

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

; ; .

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, (F-критерий):

,

Величина F-критерия связана с коэффициентом детерминации . Факторную сумму квадратов отклонений можно представить как

,

а остаточную сумму квадратов – как

Тогда значение -критерия можно выразить как

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: и .

Стандартная ошибка коэффициента регрессии определяется по формуле

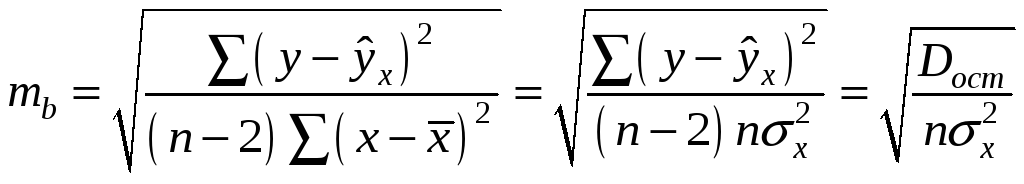
где – остаточная дисперсия на одну степень свободы.

Величина стандартной ошибки совместно с -распределением Стьюдента при степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительных интервалов.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение -критерия Стьюдента: , которое затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы .

Доверительный интервал для коэффициента регрессии определяется как . Стандартная ошибка параметра а определяется по формуле:

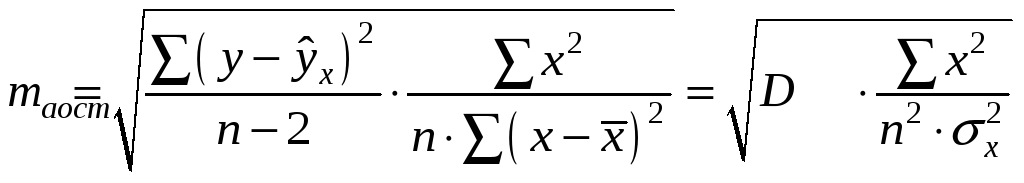
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется -критерий: , его величина сравнивается с табличным значением при степенях свободы.

Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции

, при этом .

В прогнозных расчетах по уравнению регрессии определяется предсказываемое значение как точечный прогноз при , т. е. путем подстановки в уравнение регрессии соответствующего значения , т.е. . Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки , т. е. , и соответственно интервальной оценкой прогнозного значения .

Средняя ошибка прогнозируемого индивидуального значения составит:

.

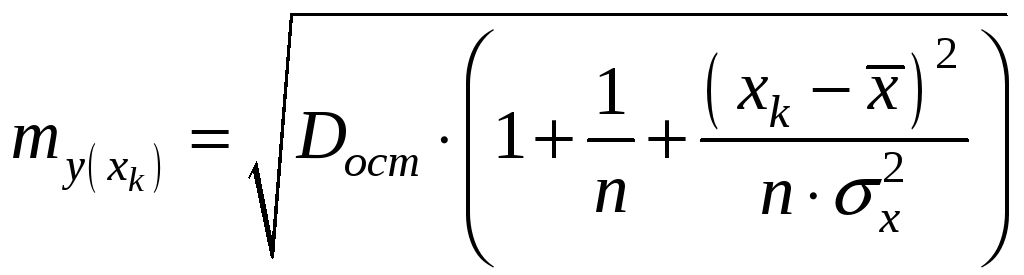При этом предельная ошибка прогноза .

Доверительный интервал прогноза строится по формуле:

.

Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т. е. и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения , а для другого она равна 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения , а для второго , ошибка аппроксимации составит 25 % для первого наблюдения и 20 % – для второго.

Поскольку может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.

Отклонения можно рассматривать как абсолютную ошибку аппроксимации, а

– как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:

Пример:

Имеются данные по двум факторам.

Требуется:

№	x	y
1	1	37
2	2	70
3	4	150
4	2	90
5	5	170
6	3	93
7	4	160
Итого	21	770

Требуется:

1. построить линейное уравнение парной регрессии y от x;

2. рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации, сделать выводы;

3. оценить качество уравнения регрессии с помощью F-критерия Фишера (α=0,05);

4. оценить статистическую значимость параметров регрессии (α=0,05);

5. построить точечный прогноз при х=4

6. оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

РЕШЕНИЕ

Расчетная таблица:

№	x	y	yx	x^2	y^2		y-		(y-)^2
1	1	37	37	1	1369	40,67	-3,67	9,9%	13,44
2	2	70	140	4	4900	75,33	-5,33	7,6%	28,44
3	4	150	600	16	22500	144,67	5,33	3,6%	28,44
4	2	90	180	4	8100	75,33	14,67	16,3%	215,11
5	5	170	850	25	28900	179,33	-9,33	5,5%	87,11
6	3	93	279	9	8649	110,00	-17,00	18,3%	289,00
7	4	160	640	16	25600	144,67	15,33	9,6%	235,11
Итого	21	770	2726	75	100018	770	0	70,7%	896,67
Среднее	3,00	110,0	389,43	10,71	14288,29			10,1%
^2	1,71	2188,29
	1,309	46,779

а) 

Построенное уравнение парной линейной регрессии: .

б) линейный коэффициент корреляции в данном случае проще найти по формуле

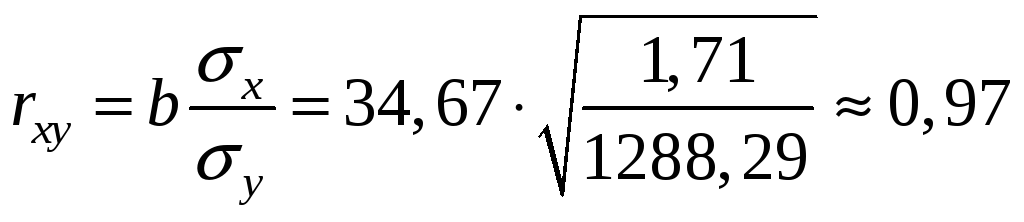, что говорит о наличии сильной прямой связи между факторами и .

Для нахождения средней ошибки аппроксимации рассчитаем сначала теоретические значения фактора по найденному в пункте а) уравнению регрессии (столбик ), затем линейные отклонения , и, наконец, относительные отклонения . Остается только найти сумму и среднее в данном столбце. Это и будет средняя ошибка аппроксимации.

Таким образом, . Данное значение дает основание считать полученное уравнение регрессии пригодным для дальнейшего использования.

в) Из формул, предложенных для расчета F-критерия, в данном случае проще всего воспользоваться следующей:

. Табличное значение при уровне значимости 0,95 . Так как найденное значение превосходит табличное (), у нас нет оснований считать модель статистически незначимой. Модель признается статистически значимой.

г) оценим статистическую значимость параметров регрессии

Сначала найдем остаточную дисперсию на одну степень свободы .

Для параметра регрессии стандартная ошибка 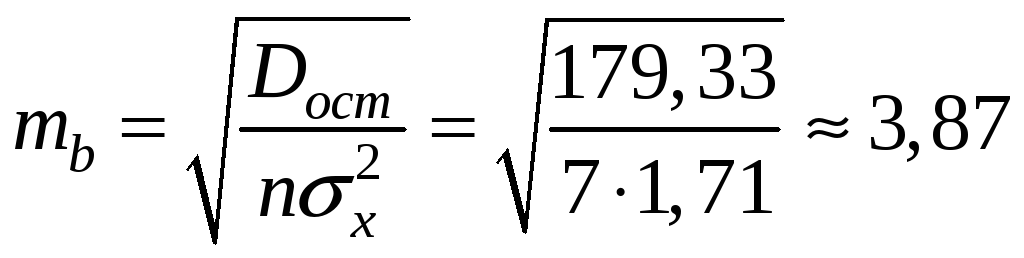, фактическое значение -критерия Стьюдента: . Для параметра , . Табличное значение t-критерия Стьюдента . Так как , а , то параметр признается статистически значимым, а параметр статистически незначимым.

д) сделаем точный прогноз по уравнению регрессии при х=4.

.

е) Найдем ошибку и доверительный интервал прогноза:

стандартная ошибка

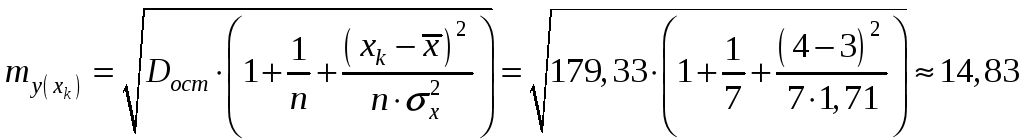
предельная ошибка

Доверительный интервал , т.е.

С вероятностью 0,95 можем гарантировать, что при значении фактора 4 единицы, фактор примет значение от 106,6 до 182,8 единиц.