мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР2 / КР-КИТ материалы / Пробные Варианты

СЕРГЕЙ ОКИШЕВ

МЕТОДИЧЕСКИЕ

МАТЕРИАЛЫ

МАТАНАЛИЗА

ИАТИТ 2013

Задания и указания

к контрольной работе КР-КИТ

«Кратные интегралы и Теория поля»

ЗАДАНИЯ:

1. Вычислить и , то есть дивергенцию и

ротор векторного поля в заданной точке пространства.

2. Вычислить двойной интеграл, перейдя в ПСК.

Область интегрирования изобразить на чертеже.

3. Построить тело Т и вычислить его объем с помощью

тройного интеграла.

4. Вычислить криволинейный интеграл второго рода (КИ-2).

Траекторию движения точки от к изобразить.

5. Найти поток П в направлении внешней нормали к

поверхности . Поверхность и ее проекцию – изобразить.

Указания

1. В задаче 1) следует сначала выписать теоретические формулы для дивергенции и ротора. Затем следует, вычисляя частные производные, получить дивергенцию и ротор поля для произвольной точки. Координаты векторного поля, т.е. функции , , могут быть определены не во всякой точке пространства! Поэтому, прежде чем подставлять точку М в полученные формулы, следует найти область определения векторного поля (пересечение областей определения его координат). В случае некорректности задачи (если в точке М поле не определено) следует сообщить об этом и вычисление конкретных значений не производить.

2. В задаче 2) сначала изображается на плоскости область интегрирования . В большинстве ситуаций следует ввести ПСК с полюсом в точке и воспользоваться формулой ФПК. В некоторых случаях удобнее оказывается сначала перенести декартову систему координат в центр круглой (кольцевой) области, а затем вводить ПСК относительно этого центра. Постоянные пределы интегрирования по переменным и определяются по исходной области . Если расстояние граничной линии от полюса является переменным, то формулу можно найти из уравнения соответствующей границы, выполнив подстановку и упростив уравнение. Затем остается вычислить составленный двукратный интеграл.

3. При построении тела Т (алгоритм СТИ) в задаче 3) обратите внимание, какие из поверхностей являются «боковыми стенками», а какие – «дном» и «крышей» заданного тела. Задачи составлены таким образом, что в пространстве удобно выбирать направление оси (). Поэтому последние две поверхности будут поверхностями входа и выхода для тройного интеграла. В задаче требуется найти объем построенного тела. Значит, подынтегральная функция . Результат должен быть доведён до конкретного числа. Это значение тройного интеграла должно быть найдено точно, например в виде: . Приближённое значение объема, вычисленное на калькуляторе, засчитано не будет.

4. В задаче 4) не следует забывать, что движению по ориентированной кривой может соответствовать изменение основной переменной от большего значения к меньшему, чего не было в обычном определенном интеграле. Результат должен быть доведён до конкретного числа. Это значение криволинейного интеграла должно быть найдено точно, например в виде: . Приближённое значение работы, вычисленное на калькуляторе, засчитано не будет.

5. В задаче 5) не следует забывать, что поток вычисляется в направлении внешней нормали к поверхности, что может давать как острый, так и тупой угол с ортом координатной оси. Поэтому контролируйте знак при переходе от поверхностного интеграла к двойному интегралу на плоскости. На ваше счастье, задача является упрощенной! Векторное поле имеет лишь одну ненулевую координату, и поток считается через единственную проекцию! Область при проектировании получается круглой или кольцевой формы. Поэтому следует выполнять СДИ в полярной системе координат, как и во второй задаче.

Желаю удачи!

Вариант Е5

ПРОБНЫЙ ВАРИАНТ ДЛЯ САМОПОДГОТОВКИ

ЗАДАЧА 1. Найти и вычислить их значения в точке М:

ЗАДАЧА 2. Вычислить двойной интеграл в ПСК.

Область интегрирования изобразить:

D:

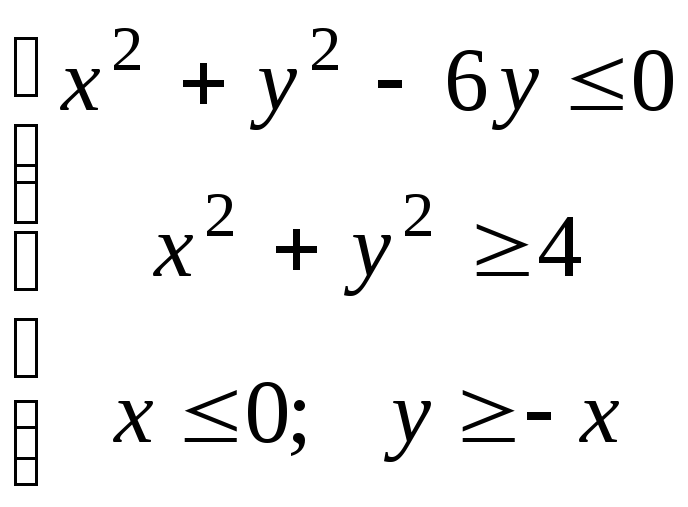
ЗАДАЧА 3.

Построить тело Т и вычислить его объем V(T) тройным интегралом:

ЗАДАЧА 4. Вычислить КИ-2. Траекторию движения

от точки к точке изобразить на чертеже:

.

ЗАДАЧА 5. Вычислить поток П в направлении внешней нормали

к поверхности . Саму поверхность и ее проекцию – изобразить на

чертеже:

.

Вариант Е6

ПРОБНЫЙ ВАРИАНТ ДЛЯ САМОПОДГОТОВКИ

ЗАДАЧА 1. Найти и вычислить их значения в точке М:

ЗАДАЧА 2. Вычислить двойной интеграл в ПСК.

Область интегрирования изобразить:

D:

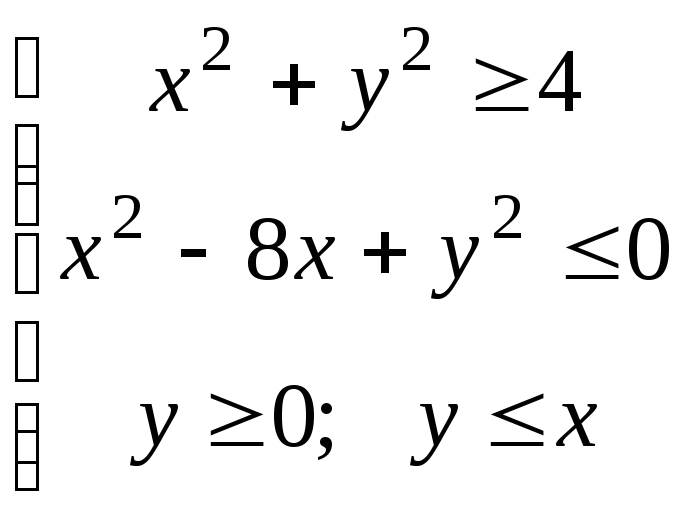
ЗАДАЧА 3.

Построить тело Т и вычислить его объем V(T) тройным интегралом:

Т:

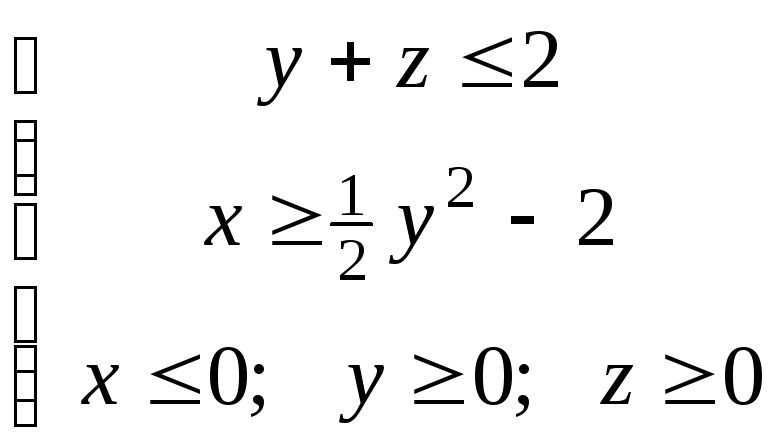
ЗАДАЧА 4. Вычислить КИ-2. Траекторию движения

от точки к точке изобразить на чертеже:

; .

ЗАДАЧА 5. Вычислить поток П в направлении внешней нормали

к поверхности . Саму поверхность и ее проекцию – изобразить на

чертеже:

.

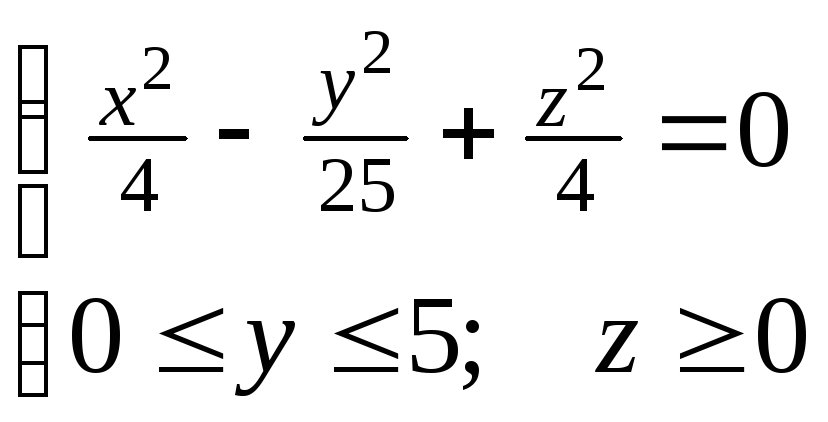РЕШЕНИЯ: Вариант Е5

ЗАДАЧА 1. Дивергенция и Ротор

Общетеоретические формулы:

; .

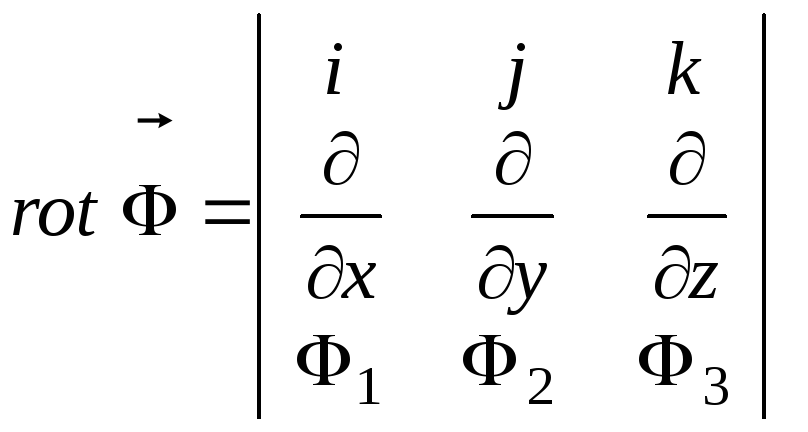Нахождение формул для данного поля:

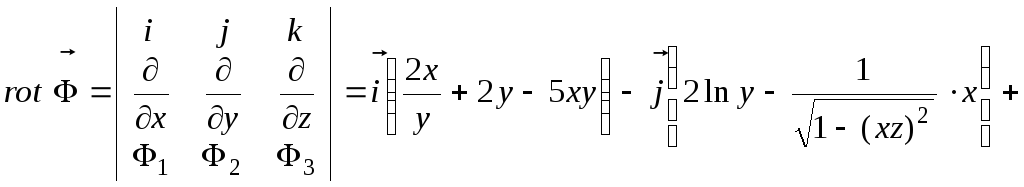
Область определения векторного поля (с учетом ротора и дивергенции):

.

Точка удовлетворяет полученным неравенствам, поэтому предложенная вычислительная задача корректна.

Окончательные вычисления:

.

==========================================================

ЗАДАЧА 2. Двойной интеграл в ПСК

Ограничения (граничные линии области D):

Строим область D на плоскости:

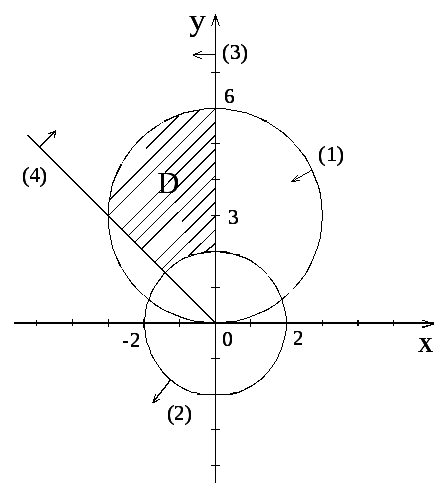
Переходим к ПСК для области D на плоскости:

ПСК: .

Для области D (границы по );

Преобразуем ограничения задачи к переменным

(1) – линия выхода из D в ПСК; (2) – линия входа в область D в ПСК.

Выполняем СДИ в ПСК: (используем алгоритм СДИ и формулу ФПК):

.

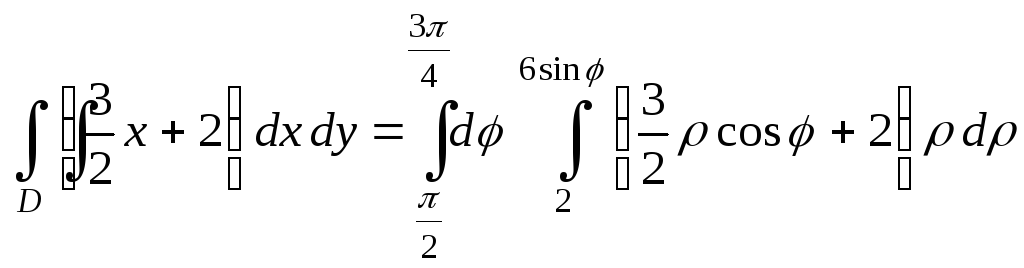Окончательные вычисления двукратного интеграла:

=

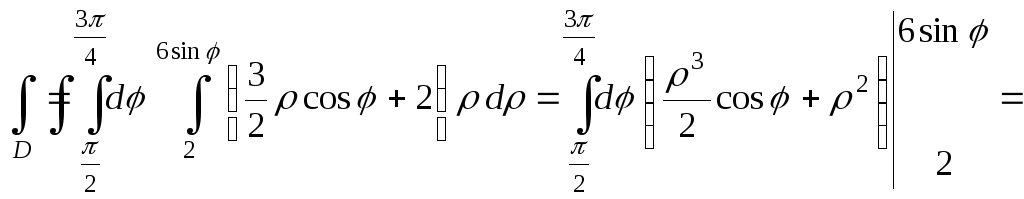
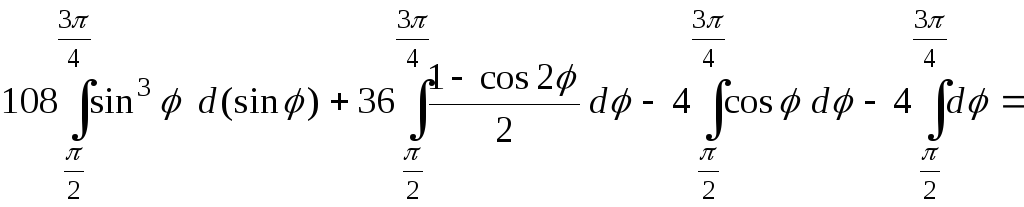
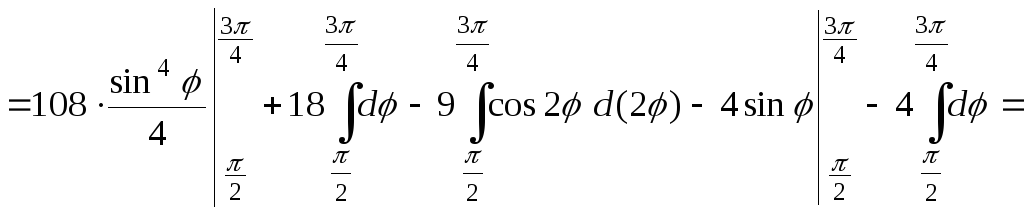
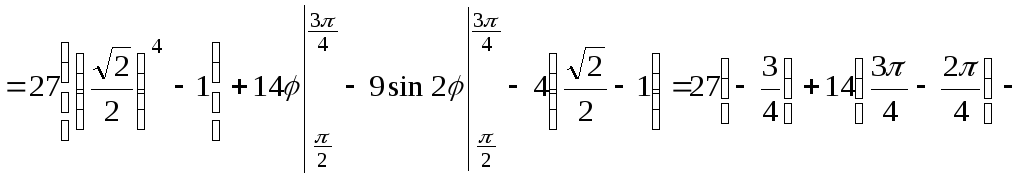
ОТВЕТ:

==========================================================

ЗАДАЧА 3. Объем тела с помощью ∫∫∫-ла

Ограничения (граничные поверхности тела Т):

Имеем: 4 плоскости и параболическую поверхность (эллиптический параболоид по оси Oz вершиной вверх).

– «дно», «основание», на котором «стоит» тело;

– «боковые стенки» тела Т, параллельные оси Oz.

Вышеперечисленные грани образуют треугольную призму, уходящую на бесконечность по оси Oz+.

– «крыша» тела Т. Чтобы изобразить часть поверхности, вырезаемую треугольной призмой, найдем значения в вершинах треугольного основания призмы.

.

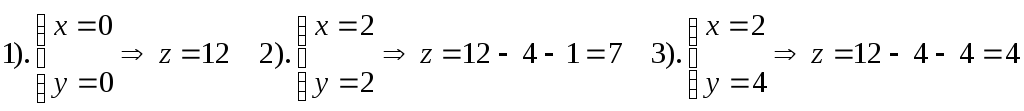Строим тело Т в пространстве:

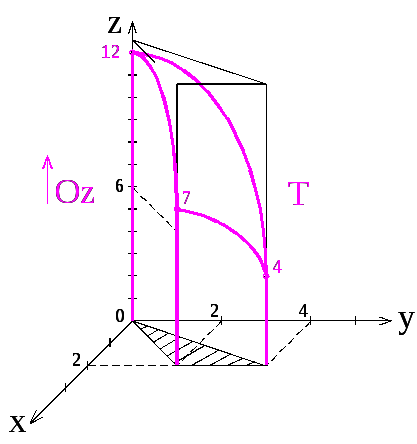
Составляем трехкратный интеграл по телу Т (алгоритм СТИ):

Поверхность входа: .

Поверхность выхода: .

Изображаем область-проекцию D на плоскости и получаем окончательную формулу трехкратного интеграла для объема тела V(T):

_________________________________________________________________

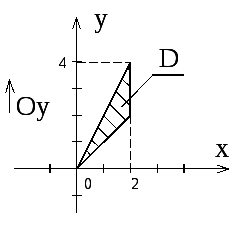
Формула вычисления объема:

.

_________________________________________________________________

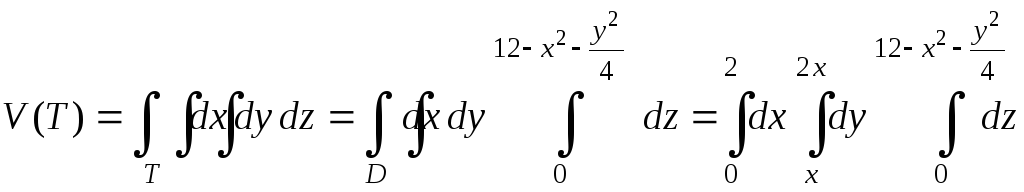Окончательные вычисления трехкратного интеграла:

=

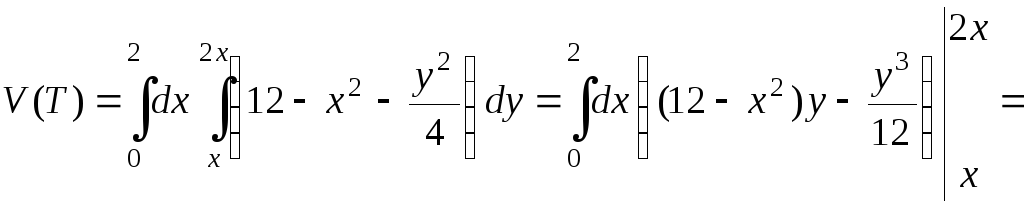
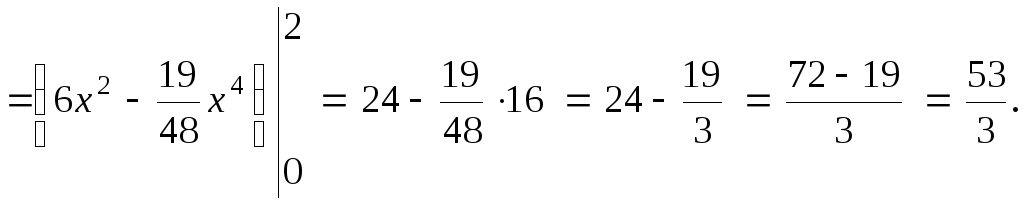
ОТВЕТ: .

==========================================================

ЗАДАЧА 4. Вычисление КИ-2 (работы поля)

Изображаем траекторию движения точки на плоскости:

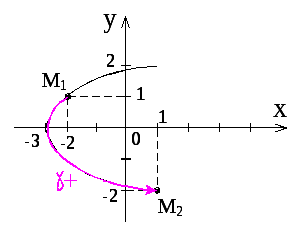
Выполняем алгоритм ВКИ-2:

.

Основная переменная .

Будем составлять определенный интеграл по .

– выразили остальное через .

– изменяется от 1 до –2 при движении от к .

Переход к определенному интегралу:

.

_________________________________________________________________

Окончательные вычисления:

=

=

_________________________________________________________________

Используем формулу интегрирования по частям для нахождения оставшегося интеграла.

_________________________________________________________________

Продолжаем вычисление определенного интеграла:

.

ОТВЕТ: .

==========================================================

ЗАДАЧА 5. Вычисление ПИ-2 (потока)

Выполняем алгоритм ВПИ-2:

, т.к. у векторного поля лишь одна составляющая – координата по оси .

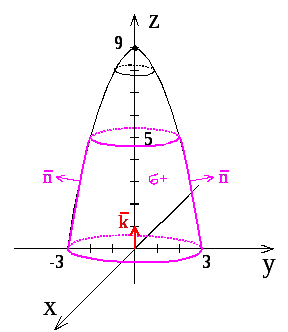
Изображаем ориентированную поверхность в пространстве:

Поверхность представляет собой часть эллиптического параболоида, расположенного вдоль оси вершиной вверх. Эта часть заключена между плоскостями и .

Независимые переменные .

Будем составлять двукратный интеграл по .

Изображаем проекцию поверхности на плоскость:

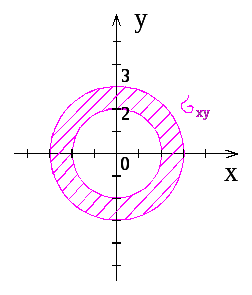
Выразили подынтегральную функцию через .

Переход к двукратному интегралу на плоскости:

.

_________________________________________________________________

Окончательные вычисления:

.

_________________________________________________________________

ОТВЕТ: . Таким образом, поток направлен «наружу»…

==========================================================

РЕШЕНИЯ: Вариант Е6

ЗАДАЧА 1. Дивергенция и Ротор

Общетеоретические формулы:

; .

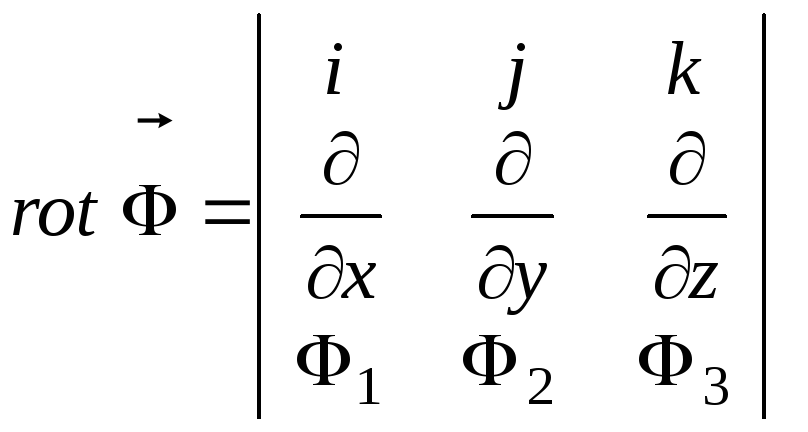Нахождение формул для данного поля:

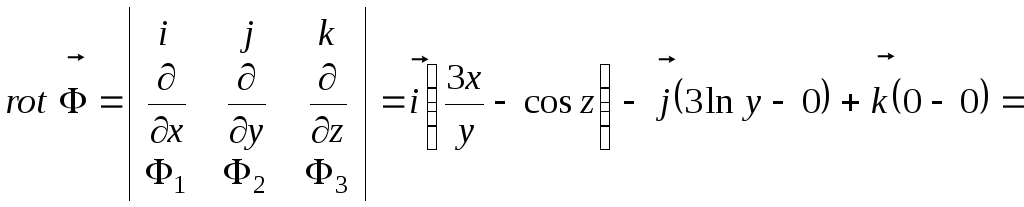
Область определения векторного поля (с учетом ротора и дивергенции):

.

Точка удовлетворяет полученным неравенствам, поэтому предложенная вычислительная задача корректна.

Окончательные вычисления:

.

==========================================================

ЗАДАЧА 2. Двойной интеграл в ПСК

Ограничения (граничные линии области D):

Строим область D на плоскости:

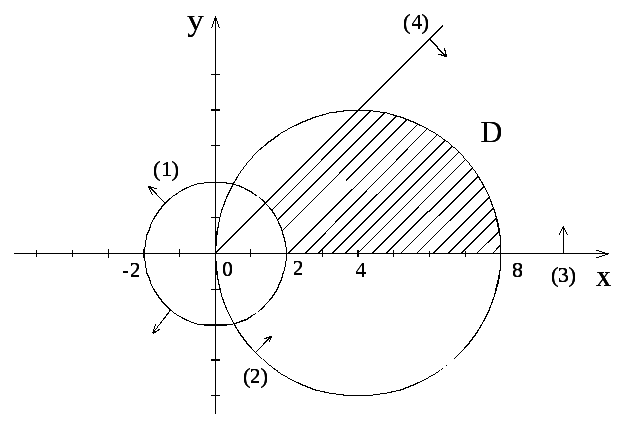
Переходим к ПСК для области D на плоскости:

ПСК: .

Для области D (границы по );

Преобразуем ограничения задачи к переменным

(1) – линия входа в область D в ПСК; (2) – линия выхода из D в ПСК.

Выполняем СДИ в ПСК: (используем алгоритм СДИ и формулу ФПК):

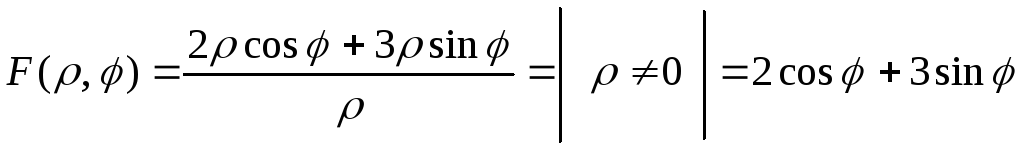. Поэтому

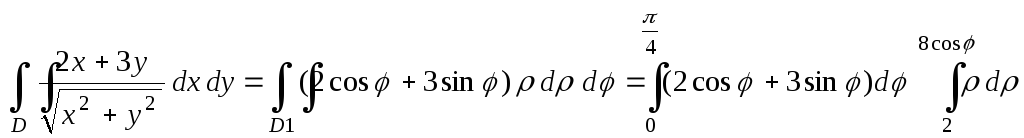
Окончательные вычисления двукратного интеграла:

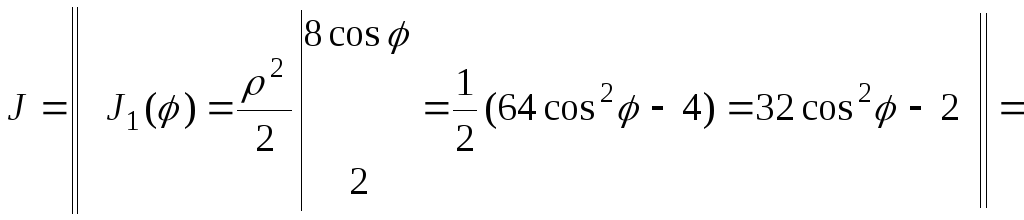
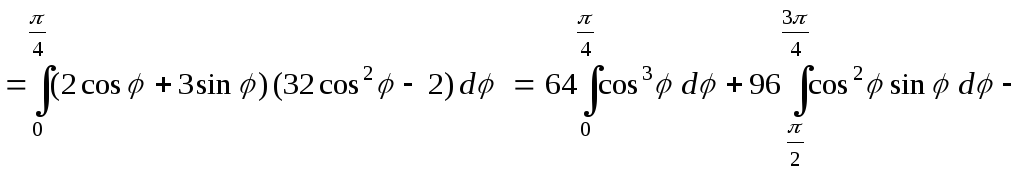
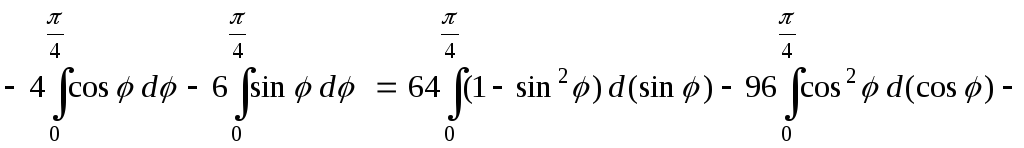
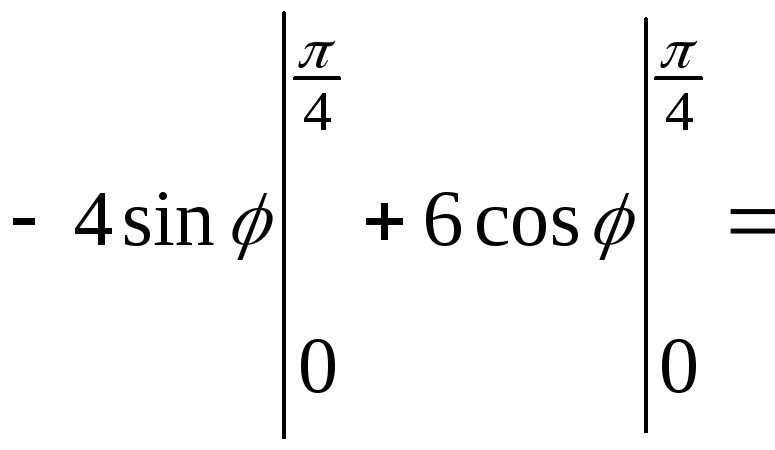
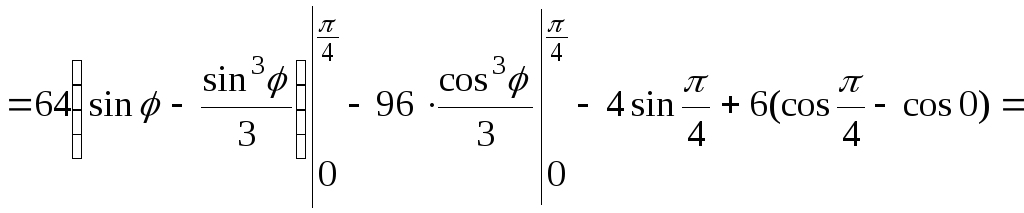
ОТВЕТ:

==========================================================

ЗАДАЧА 3. Объем тела с помощью ∫∫∫-ла

Ограничения (граничные поверхности тела Т):

Имеем: 4 плоскости и параболический цилиндр вдоль оси Oz .

– «дно», «основание», на котором «стоит» тело;

– «боковые стенки» тела Т вдоль оси Oz.

– наклонная плоскость, «крыша» тела Т.

Четыре плоские грани образуют треугольную призму, уходящую на бесконечность по оси Ox–, но параболический цилиндр отрезает от нее конечную часть, содержащую начало координат. Это и есть тело Т.

Строим тело Т в пространстве:

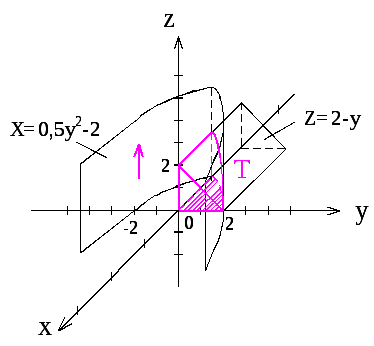
Составляем трехкратный интеграл по телу Т (алгоритм СТИ):

Поверхность входа: .

Поверхность выхода: .

Изображаем область-проекцию D на плоскости и получаем окончательную формулу трехкратного интеграла для объема тела V(T):

_________________________________________________________________

Формула вычисления объема:

.

_________________________________________________________________

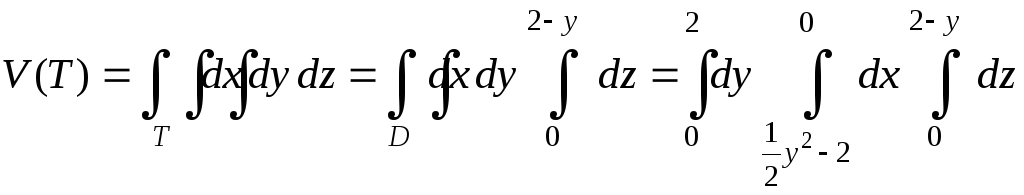Окончательные вычисления трехкратного интеграла:

= .
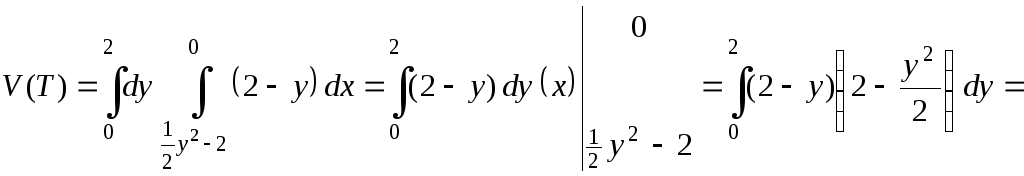
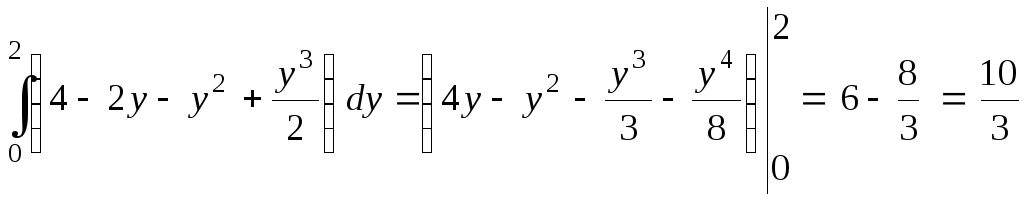