Тема 5. Транспортная задача

Постановка транспортной задачи

Симплекс-метод является универсальным методом решения задач линейного программирования. Однако существуют классы задач, обладающие специфическими свойствами, для которых разработаны более простые методы решения. К такому типу относится задача, получившая название транспортной.

Пусть имеется m поставщиков однородного груза с запасами (мощностями) единиц соответственно. Этот груз необходимо доставить n потребителям , необходимое количество груза для которых (емкости) составляет . Стоимости с_ij перевозок единицы груза от i-го поставщика к j-му потребителю считаются заданными. Условия задачи представлены в таблице вида

		b2
a2
am

Требуется составить такой план перевозок (т.е. указать количество перевезенного груза от каждого поставщика к каждому потребителю), при котором будут полностью разгружены поставщики и удовлетворены потребители, а транспортные издержки будут минимальны.

Если суммарная мощность поставщиков равна суммарной емкости потребителей, т.е. 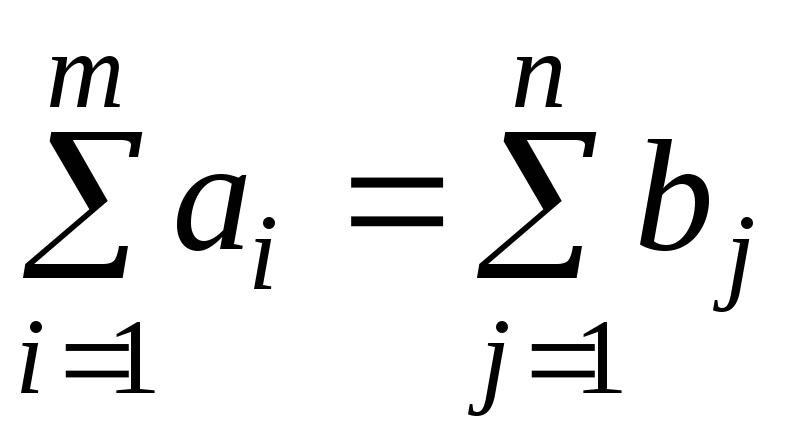, то модель транспортной задачи называется закрытой, при нарушении этого условия — открытой.

Закрытая транспортная задача

Рассмотрим задачу закрытого типа. Обозначим количество груза, перевозимого от i-го поставщика к j-му потребителю, через.

Составим математическую модель задачи.

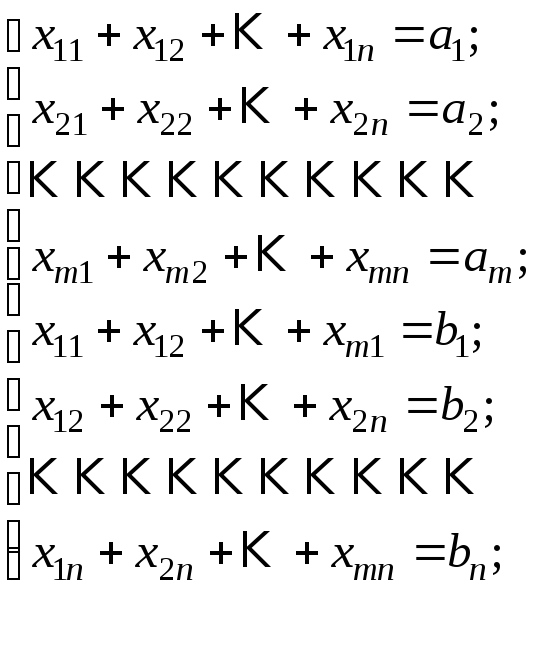(1)

(2)

(3)

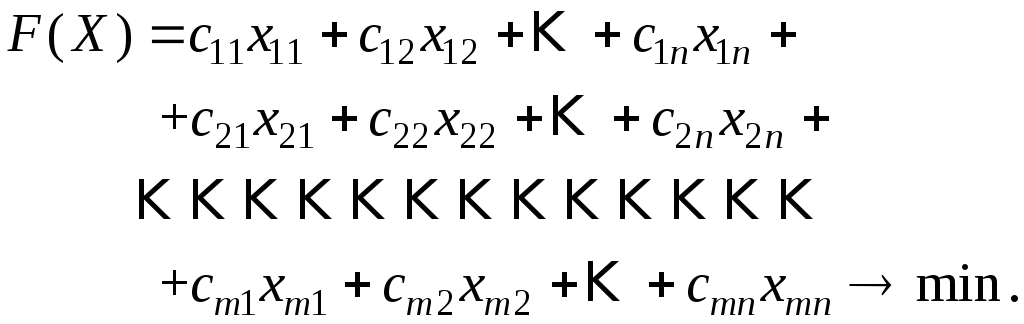(4)

Первые m уравнений системы (1) соответствуют ограничениям по запасам поставщиков, последние n — ограничениям потребителей; условие неотрицательности (2) следует из экономического смысла неизвестных ; уравнение (2) означает, что транспортная задача является закрытой. Целевая функция (4) выражает суммарную стоимость перевозок.

Математически транспортная задача (1)—(4) ставится следующим образом: среди множества планов системы линейных уравнений (1), (3) и неравенств (2) найти такой план 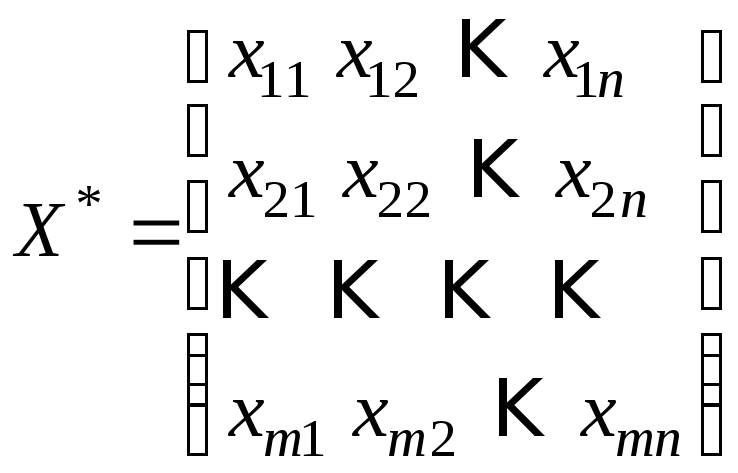, который минимизирует целевую функцию (4).

Таким образом, транспортная задача является задачей линейного программирования и может быть решена симплекс-методом, алгоритм которого состоит из трех шагов:

1. Построение начального плана.

2. Проверка плана на оптимальность. Если план оптимален, то задача решена; в противном случае — переход к п.3.

3. Построение нового плана с меньшей (или равной) стоимостью перевозок.

Специфические особенности системы ограничений транспортной задачи привели к разработке упрощенного метода решения на каждом шаге алгоритма.

Пример 1. Необходимо осуществить перевозки однородного груза от 4-х поставщиков 3-м потребителям, запасы и потребности которых, а также стоимости единичных перевозок заданы таблицей:

	12	9	19
9	10	3	10
8	7	8	12
12	5	5	8
11	2	1	7

Требуется построить такой план перевозок, при котором суммарная стоимость будет наименьшей.

1. Построение начального плана.

Прежде всего проверим, является ли задача закрытой.

9+8+12+11=40;

12+9+11=40.

Поскольку 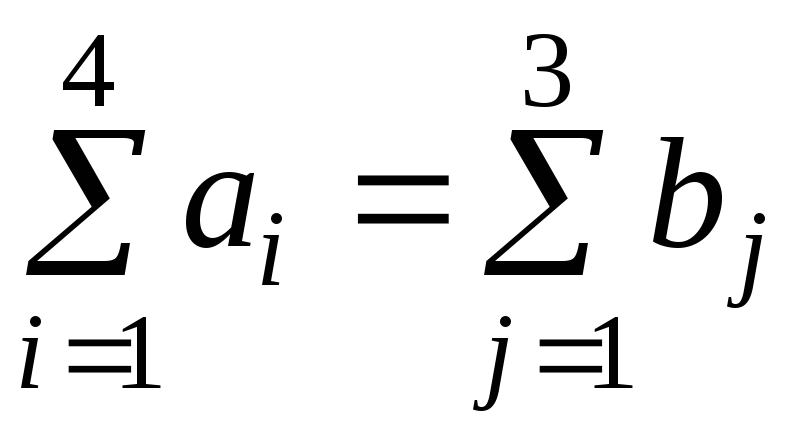, мы имеем дело с закрытой задачей.

Решение будем строить непосредственно в транспортной таблице 7, которая имеет вид:

Таблица 7.

Поставщики		Потребители
			b2

где a_i — мощность поставщиков, b_j — емкость потребителей, с_ij —стоимость единичной перевозки, а х_ij — количество перевозимого груза от А_i поставщика к B_j потребителю, i=1…m, j=1…n.

Начальный план составим методом наименьшей стоимости.

Из всей таблицы выбираем наименьшую стоимость единичной перевозки с_ij и в соответствующую ей клетку помещаем наименьшее из чисел и . Тогда или будет полностью исчерпан запас груза поставщика и в остальных клетках i -ой строки можно поставить прочерк, или потребности потребителя будут полностью удовлетворены и можно поставить прочерк в оставшихся клетках j-го столбца.

Из незаполненных клеток снова выбираем клетку с наименьшей стоимостью, и процесс распределения грузов повторяем, пока все запасы поставщиков не будут распределены, а потребности потребителей полностью удовлетворены. (Если клеток с одинаковой стоимостью несколько, в первую очередь заполняется клетка с наибольшей возможной поставкой.)

В нашем примере наименьшую стоимость перевозки с₄₂=1 имеет клетка (4;2). Потребность в грузе потребителя B₂ составляет 9, а запас груза поставщика А₄ 11 единиц. Наибольшая из возможных поставок =9 (наименьшее из чисел 11 и 9). Записываем =9 в таблицу и в оставшихся клетках второго столбца ставим прочерк, т.к. потребности B₂ будут полностью удовлетворены. У поставщика А₄ остается в запасе 2 единицы груза.

Далее заполняем клетку (4;1) с с₄₁=2. Поставку х₄₂ определим как наименьшее из чисел 12 и 2 (остаток груза А₄), х₄₂=2. Потребителю В₁ необходимо завезти еще 10 единиц груза, а возможности поставщика А₄ будут исчерпаны полностью, в клетке (4;3) ставим прочерк.

Из оставшихся клеток наименьшую стоимость имеет клетка (3;1) с с₃₁=5. Запас груза А₃ равен 12, потребность В₁ 10 единиц, следовательно х₃₁=10. Потребности В₁ удовлетворены полностью, в остальных клетках первого столбца ставим прочерки. Оставшиеся у А₃ 2 единицы поместим в (3;3), т. е. х₃₃=2. Далее вносим в таблицу х₂₃=8, х₁₂=9.

Таблица 8 представляет начальный план задачи Х₁. (Полезно проверить, что сумма поставок по столбцам равна соответствующим мощностям потребителей, сумма поставок по строкам — емкостям поставщиков.)

Таблица 8. План Х₁.

40 40
		12	9	19
	9	10 —	3 —	10 9
	8	7 —	8 —	12 8
	12	5 10	5 —	8 2
	11	2 2	1 9	7 —

Заполненные клетки таблицы соответствуют базисным переменным, а пустые — свободным переменным из системы ограничений (1) (свободные переменные равны нулю). Поскольку система (1) содержит m+n–1 линейно независимых уравнений, то и число базисных переменных будет таким же, (m — число поставщиков, n — число потребителей). План с m+n–1 заполненными (базисными) клетками называется невырожденным, при меньшем числе заполненных клеток — вырожденным. Для того чтобы снять вырождение, необходимо в пустые клетки записать нулевые перевозки, дополнив число базисных переменных до количества m+n–1. Ноль можно поставить только в ту пустую клетку, которая не будет образовывать цикла вместе с уже заполненными клетками.

Циклом называется замкнутая ломаная, вершины которой находятся в клетках, а звенья располагаются вдоль строк и столбцов; в каждой вершине встречаются два звена, одно из которых проходит вдоль строки, а другое — вдоль столбца. Начало и конец ломаной совпадают; она может самопересекаться.

Проверим вырожденность плана нашей задачи: мы имеем 4-х поставщиков и 3-х потребителей, для невырожденного плана число заполненных клеток должно составлять 4+3–1=6. У нас 6 заполненных клеток, следовательно, план невырожденный.

Подсчитаем суммарную стоимость перевозок плана Х₁:

и делаем следующий шаг.