Тема 4. Симплекс-метод решения задачи линейного программирования

Основная и каноническая задачи лп

Ограничениями основной задачи ЛП являются уравнения, задача имеет вид:

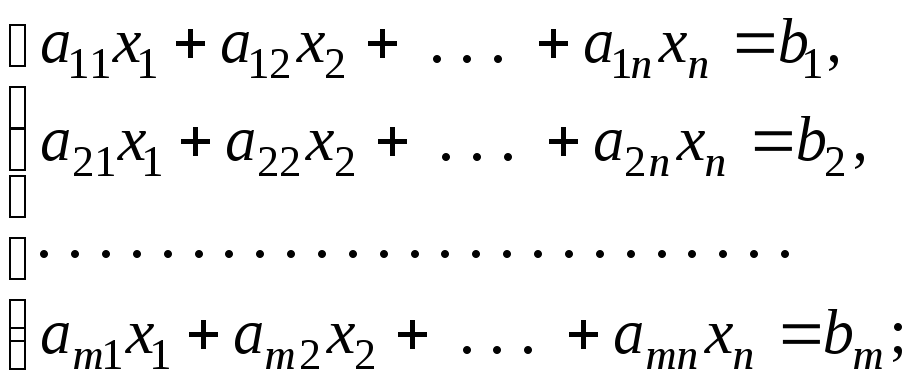(1)

(2)

(3)

Система (1) содержит m уравнений с n неизвестными. Будем считать, что m<n, все m уравнений линейно независимы. (Напомним, что линейная независимость уравнений предполагает невозможным представить одно уравнение через линейную комбинацию остальных). Тогда любые m переменных можно выбрать (сделать) базисными, оставшиеся n – m переменных — свободными. В каждой системе существует конечное число наборов базисных переменных.

Основная задача (1) — (3) является канонической при выполнении следующих условий:

1. b_i; ;

2. в каждом уравнении системы ограничений (1) есть базисная переменная. Базисной является переменная, которая встречается в системе уравнений только один раз и входит в уравнение с коэффициентом, равным +1;

3. целевая функция максимизируется:.

План, в котором все свободные переменные равны нулю, называется базисным планом. Каждому базисному плану соответствует угловая точка многогранника решений. Если оптимальное решение задачи ЛП существует, то оно соответствует хотя бы одной угловой точке и совпадает, по крайней мере, с одним базисным планом.

Таким образом, для решения задачи ЛП необходимо перебрать все вершины многоугольника планов и выбрать ту, на которой целевая функция достигает оптимального значения. Перебор вершин можно проводить не хаотично, а последовательно улучшая решения (т.е. значение целевой функции на каждом последующем плане по крайней мере не меньше, чем на предыдущем) — в этом состоит симплекс-метод решения задачи ЛП.

Поскольку симплекс-метод применяется для решения канонических задач, необходимо научиться приводить общую и основную задачу к канонической форме. Для этого необходимо:

1. Убедиться, что все b_i0, (в противном случае умножить соответствующее уравнение на (–1)).

2. Для перехода от неравенств системы ограничений общей задачи к уравнениям основной задачи в левую часть каждого неравенства вводят дополнительную неотрицательную переменную: со знаком «+» в неравенства типа «», со знаком «» в неравенства типа «».

Если после этого каждое уравнение системы ограничений будет содержать базисную переменную, то получим систему ограничений канонической задачи, такая задача называется задачей с естественным базисом.

3. Каноническая задача подразумевает максимизацию целевой функции, поэтому если поставлена задача , то следует рассматривать функцию . (Очевидно, что функция F(X) достигает наименьшего значения при тех же неизвестных , что и — наибольшего.)

Составление симплекс-таблицы

Симплекс-метод разработан для решения канонической задачи ЛП и проводится в симплекс-таблице.

Пусть каноническая задача имеет вид:

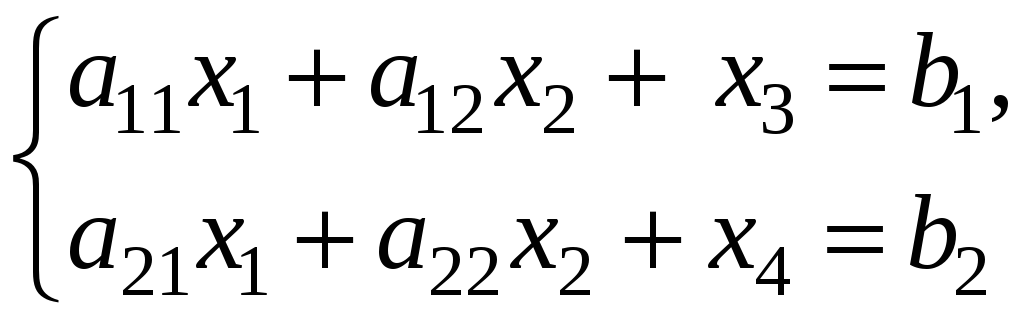(1)

.

Запишем ее в симплекс-таблицу. Каждому уравнению системы ограничений соответствует строка таблицы.

В первый столбец выписывается название переменной, которая является базисной для данного уравнения; в первом уравнении это х₃, во втором — переменная х₄. Во второй столбец записываются свободные члены уравнений b_i, остальные элементы таблицы равны коэффициентам при соответствующих неизвестных.

В последнюю строку таблицы записывают целевую функцию , эта строка называется индексной.

Элементы индексной строки заполняются по следующему правилу. Слева от симплекс-таблицы выписываются коэффициенты при базисных переменных целевой функции, над верхней строкой симплекс-таблицы выписываются коэффициенты при соответствующих переменных целевой функции. Элементы индексной строки находятся по правилу: коэффициенты c_i (слева от таблицы) умножаются на элементы соответствующего столбца, полученные произведения складываются и затем вычитается коэффициент сверху (для столбца свободных членов коэффициент сверху прибавляется), табл.1.

Таблица 1.

		c0	0	0	с3	с4
	баз.	своб.	х1	х2	х3	х4
с3	х3	b1	a11	a12	1	0
с4	х4	b2	a21	a22	0	1
		d0	d1	d2	d3	d4

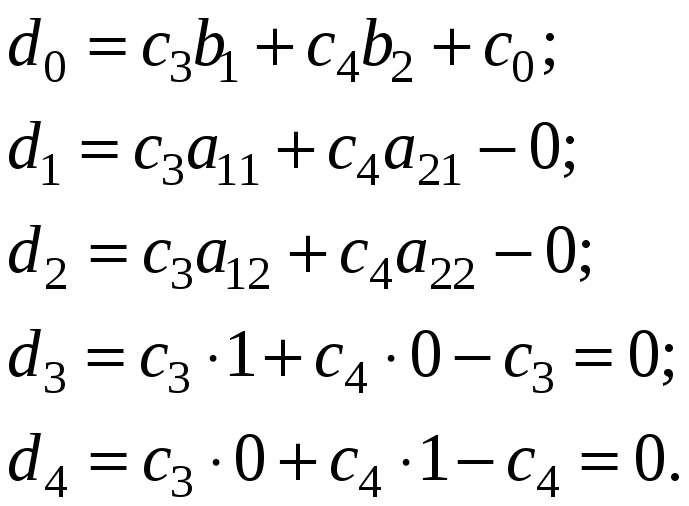(2)

Согласно (2), элементы индексной строки, соответствующие базисным столбцам, всегда равны 0, их можно сразу вписывать в таблицу.