Лекция 8 Введение в теорию алгоритмов 4 ч

Лекция 1 Введение в теорию алгоритмов

Теория алгоритмов - это наука, изучающая общие свойства и закономерности алгоритмов, разнообразные формальные модели их представления. На основе

формализации	понятия	алгоритма		возможно	сравнение	алгоритмов	по
эффективности, проверка их эквивалентности, определение областей применимости.
Разработанные	в 1930-х	годах	разнообразные формальные модели алгоритмов
(Пост, Тьюринг,	Черч), равно		как и	предложенные 1950в -х		годах модели

Колмогорова и Маркова, оказались эквивалентными в том смысле, что любой класс проблем, разрешимых в одной модели, разрешимы и в другой.

1.1 Исторический обзор

Первым дошедшим до нас алгоритмом в его интуитивном понимании– конечной последовательности элементарных действий, решающих поставленную задачу, считается предложенный Евклидом вIII веке до нашей эры алгоритм нахождения

наибольшего	общего	делителя	двух чисел(алгоритм	Евклида). В течение
длительного	времени,	вплоть до	началаXX века	само слово«алгоритм»

употреблялось в устойчивом сочетании«алгоритм Евклида». Для описания пошагового решения других математических задач использовалось слово «метод».

Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя (1931 год - теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Геделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.

Первые фундаментальные работы по теории алгоритмов были опубликованы независимо друг от друга 1936в году Аланом Тьюрингом, Алоизом Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и лямбдаисчисление Черча были эквивалентными формализмами(система обозначений)

алгоритма.	Сформулированные			ими	тезисы(Поста			и	Черча-Тьюринга)
постулировали		эквивалентность		предложенных			ими	формальных			систем
интуитивного		понятия	алгоритма. Важным			развитием		этих		работ	ст
формулировка и доказательство алгоритмически неразрешимых проблем.
В 1950-е годы существенный вклад в						теорию алгоритмов				внесли раб
Колмогорова и Маркова.
К 1960-70-ым годам оформились следующие направления в теории алгоритмов:
• Классическая теория алгоритмов (формулировка задач в терминах формальных
языков, понятие задачи разрешения, введение сложностных классов);
• Теория	асимптотического			анализа		алгоритмов(понятие			сложности		и
трудоёмкости		алгоритма,	критерии	оценки		алгоритмов, методы			получения
асимптотических		оценок, в		частности			для	рекурсивных			алгор,
асимптотический		анализ	трудоемкости		или	времени		выполнения),		развитие

которой внесли существенный вклад Кнут, Ахо, Хопкрофт, Ульман, Карп;

• Теория практического анализа вычислительных алгоритмов(получение явных функции трудоёмкости, интервальный анализ функций, практические критерии качества алгоритмов, методика выбора рациональных алгори).

Основополагающей работой в этом направлении, следует считать фундаментальный труд Д. Кнута «Искусство программирования для ЭВМ».

1.2 Цели и задачи теории алгоритмов

Обобщая результаты различных разделов теории алгоритмов можно выделить следующие цели и соотнесенные с ними задачи, решаемые в теории алгоритмов:

• формализация понятия «алгоритм» и исследование формальны алгоритмических систем;

•формальное доказательство алгоритмической неразрешимости ряда задач;

•классификация задач, определение и исследование сложностных классов;

•асимптотический анализ сложности алгоритмов;

•исследование и анализ рекурсивных алгоритмов;

•получение явных функций трудоемкости в целях сравнительного анализ алгоритмов;

•разработка критериев сравнительной оценки качества алгоритмов.

1.3 Практическое применение результатов теории алгоритмов

Полученные в теории алгоритмов теоретические результаты находят достаточно широкое практическое применение, при этом можно выделить следующие два аспекта:

Теоретический аспект: при исследовании некоторой задачи результаты теории алгоритмов позволяют ответить на вопросявляется ли эта задача в принципе алгоритмически разрешимой.

Для	алгоритмически неразрешимых задач возможно их				сведение к		за
останова машины Тьюринга.
В	случае	алгоритмической	разрешимости	задачиследующий		важный
теоретический вопрос - это вопрос о принадлежности этой задачи к классуNP-
полных	задач,	при утвердительном ответе на		который, можно	говорить		о

существенных временных затратах для получения точного решения для больших размерностей исходных данных.

Практический аспект: методы и методики теории алгоритмов( основном разделов асимптотического и практического анализа) позволяют осуществить:

•рациональный выбор из известного множества алгоритмов решения данной задачи с учетом особенностей их применения(например, при ограничениях на размерность исходных данных или объема дополнительной памяти);

•получение временных оценок решения сложных задач;

•получение достоверных оценок невозможности решения некоторой задачи за определенное время, что важно для криптографических методов;

•разработку и совершенствование эффективных алгоритмов решения задач в области обработки информации на основе практического анализа.

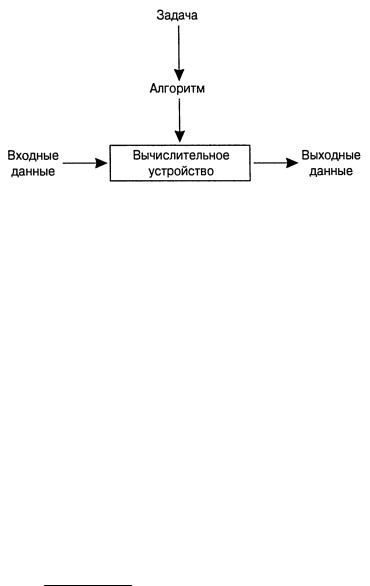
1.4 Формализация понятия алгоритма

Во всех сферах своей деятельности, и частности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата (мы можем трактовать это как первоначальное или интуитивное опред алгоритма.)

Алгоритм - это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных.

Определение можно проиллюстрировать с помощью простой схемы:

Алгоритм — это последовательность команд, позволяющих получить из корректных входных данных требующиеся выходные данные за ограниченны промежуток времени.

На схеме "вычислительное устройство" — некоторое абстрактное устройство (или человек), способное распознать эти инструкции и выполнить предписываемые ими действия. Однако следует иметь в виду, что до появления компьютеров под

термином	"вычислительное	устройство" понимался	человек, выполняющий
числовые	расчеты. Естественно, если речь идет о		современности, под словом
"вычислительное устройство" понимается компьютер.

Тем не менее нужно обратить внимание на, чтото, хотя большая часть алгоритмов в конечном счете предназначена для реализации на компьютере, само понятие алгоритма никак не связано с этим допущением.

Пусть D - область (множество) исходных данных задачи, а R - множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение D → R.

Поскольку такое отображение может быть не полным, то вводятся следующие понятия:

Алгоритм называется частичным, если мы получаем результат только дл

некоторых d D и полным алгоритмом, если алгоритм получает правильный

результат для всех d D.
В теории	алгоритмов		были введены различные формальные	определ
алгоритма
(Колмогоров):	Алгоритм -		это всякая система вычислений, выполняемых	по

строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.

(Марков): Алгоритм - это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.

Различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:

•алгоритм должен содержать конечное количество элементарно выполнимых предписаний;

•алгоритм должен выполнять конечное количество шагов при решении задачи;

•алгоритм должен быть единым для всех допустимых исходных данных;

•алгоритм должен приводить к правильному по отношению к поставленной задаче решению.

Другие формальные определения понятия алгоритма связаны с введен специальных математических конструкций(машина Поста, машина Тьюринга, рекурсивно-вычислимые функции Черча) и постулированием тезиса эквивалентности такого формализма и понятия «алгоритм».

Можно выделить семь параметров, характеризующих алгоритм:

1)совокупность возможных исходных данных;

2)совокупность возможных результатов;

3)совокупность возможных промежуточных результатов;

4)правило начала;

5)правило непосредственной переработки;

6)правило окончания;

7)правило извлечения результата.

Общие свойства алгоритмов.
1) Всякий алгоритм применяется	к входным данным и имеет	результа
выходные данные. На элементарных	шагах появляются промежуточные	данные.

Данные должны быть специфицированы, в частности, указан алфавит данных и способы построения сложных данных из простых. Примерами данных могут быть числа, массивы чисел, изображения на экране и т. д.

2) Единицы объема данных и памяти ЭВМ должны быть согласованы.

В прикладных алгоритмических моделях объем данных можно измерять числом ячеек памяти, в которых данные размещены. При этом исходят из того, что память ЭВМ состоит из одинаковых ячеек, каждая из которых может содержать один или несколько символов алфавита данных.

3) Элементарные шаги алгоритма состоят из базовых операций, число которых конечно.

В частности, под операциями можно подразумевать машинные команд, входящие в состав системы команд ЭВМ. В языках программирования высокого уровня базовые операции могут быть представлены операторами, входящими в состав синтаксиса данного языка программирования.

4) Последовательность шагов алгоритма должна быть однозначной.

Не допускается произвола при выборе очередного шага алгоритма. Должны быть зафиксированы начальный и конечный шаги алгоритма. Возможны циклы (замкнутые подпути). Все шаги, которые встречаются в алгоритме, можно разделить на условные и безусловные. После безусловного действия либо выполняется действие, расположенное вслед за ним в описании, либо однозначно указывается, какой шаг надо выполнять следующим. Условное действие связано с проверкой

условия и указывает, какое действие должно следовать за ним в зависимости от результата проверки.

5) Если способ получения результата на каком-либо шаге неприменим, то должно быть указано, что считать результатом выполнения алгоритма.

Говорят, что алгоритм применим к допустимому исходному данном,уесли с его

помощью можно перейти от исходного данного к искомому результату. Если результата нет, алгоритм — неприменим. Понятие применимости отвлечено от реальной ограниченности времени и ресурсов, требуется лишь конечность числа шагов и принципиальная возможность их выполнения. При этом используется термин потенциальной выполнимости алгоритма. Невыполнимость может состоять, например, в невозможности деления на нуль.

6)Начальная система величин может выбираться из некоторого потенциально бесконечного множества, что должно являть массовость алгоритма.

7)Детерминированность означает, что при одних и тех же исходных данных получается один и тот же конечный результат.

8)Корректность алгоритма состоит в правильности полученных с помощью него результата. Кроме того, алгоритм должен быть обоснован и согласован с фактами и положениями данной области науки или техники.

Для машинной реализации алгоритма необходимо записать его на я программирования, то есть составить программу. Путь от описания алгоритма к результату его выполнения проходит через транслятор– специальную программу, которая перерабатывает запись алгоритма в последовательность машинных команд.

Алгоритм является фундаментальным понятием информатики. Имеется три крупных класса алгоритмов:

	1) вычислительные (работают с числами, числовыми матрицами и другими
числовыми структурами);
	2)информационные (работают с большими объемами данных—базами данных –
решают задачи поиска, записи, сортировки записей);
	3)управляющие (формируют управленческие воздействия на внешние процессы в
соответствии с поступающей от них информацией).
	Теорию алгоритмов можно разделитьна дескриптивную(качественную) и
метрическую (количественную).
	Первая исследует алгоритмы с точки зрения устанавливаемого ими соответствия
между исходными данными и результатами. К ней относятся, в										частности,
проблемы построения алгоритма, обладающего теми или иными свойствами,
алгоритмические проблемы.
	Вторая исследует алгоритмы с точки зрения сложности как самих алгоритмов, так
и	задаваемых	ими	вычислений, то		есть		процессов			последовательно
преобразования конструктивных объектов.
	В качестве примеров, иллюстрирующих понятие алгоритма, рассмотрим три
способа решения		одной	и той же	задачи— поиска			НОД		двух	целых чисел.
(Наибольшим общим делителем(НОД) для двух целых чиселm и n называется
наибольший из их общих делителей.)
	Обозначим функцию		поиска НОД	двух	неотрицательных				целых чиселm и n

(причем m и n не могут одновременно равняться нулю) через gcd (m, n) (стандартное обозначение НОД от англ. Greatest Common Divisor). По определению эта функция должна найти наибольшее целое число, которое делится без остатка как наm так и на n.

Древнегреческий математик Евклид описал алгоритм решения этой задачи в одном из своих трудов под названием Начала.

Выражаясь современным языком, алгоритм Евклида основан на рекуррентном вычислении (вычисление на основе значений предыдущихчленов

последовательности) следующего равенства: gcd (m ,n) = gcd (n, m mod n).

Здесь выражение (m mod n) является остатком от деленияm на n. Выполнение алгоритма заканчивается, когда выражение (m mod n) становится равным нулю.

Поскольку gcd (m, 0) = m, последнее полученное значениеm будет также являться НОД исходных чисел m и n.

Например, вычисление НОД пары чисел(60, 24) можно выполнить следующим

образом:
gcd (60,24) = gcd (24,12) = gcd (12,0) = 12.
Приводем	более	структурированное	описание	рассматриваемого
алгоритма.
Вычисление НОД чисел m и n при помощи алгоритма Евклида
Шаг 1 Если n = 0, вернуть m в качестве			ответа и закончить работу; иначе
перейти к шагу 2.
Шаг 2 Поделить нацело m на n и присвоить значение остатка переменной r.
Шаг 3 Присвоить		значениеn переменной m, а значение r — переменной n.
Перейти к шагу 1.

В качестве альтернативы запишем тот же алгоритм в виде псевдокода.

Алгоритм Euclid (m, n)

//Алгоритм Евклида вычисляет значение функции gcd (m ,n)

//Входные данные: два неотрицательных целых числа m и n,

// которые не могут одновременно быть равны нулю // Выходные данные: наибольший общий делитель чисел m и n

while n ≠ 0 do r ← m mod n m ← n

n ← r return m

То, что в конечном счёте выполнение алгоритма Евклида завершится следует из того, что на каждом шаге итерации значение второго числа (n)парыбудет уменьшаться, причем, по определению, оно не может быть меньше нуля. Новое значение числа n, получаемое на следующей итерации в результате вычисления выражения (m mod n), будет всегда меньше, чем предыдущее значение числаn. Следовательно, рано или поздно значение второго числа пары станет равным0, и выполнение алгоритма завершится.

Как и при решении большинства других, существуетзадач несколько алгоритмов вычисления НОД. Рассмотрим два других способа решения этой задачи.

Первый из них основан на подборе наибольшего целого числа— такого, чтобы числа т и п делились на него без остатка. Очевидно, что такой общий делитель не может быть больше наименьшего из чисел пары, которое можно записать какt = min{ m, n }. Поэтому выполнение алгоритма можно начать с проверки того, делятся ли оба числа, m и n, на t без остатка. Если это так, то число t является ответом; если нет, нужно уменьшить значение t на единицу и снова выполнить проверку.

Например, для рассмотренной выше пары чисел(60,24), выполнение алгоритма начинается с проверки числа 24, затем — 23 и т.д. до тех пор, пока значение числа t не станет равным 12, после чего алгоритм должен завершить свою работу.

Вычисление НОД чисел m и n методом последовательного перебора Шаг 1 Присвоить значение функции min { m, n } переменной t.

Шаг 2 Разделить m на t. Если остаток равен нулю, перейти к шагу3; иначе перейти к шагу 4.

Шаг 3 Разделить n на t. Если остаток равен нулю, вернуть t в качестве ответа и закончить работу; иначе перейти к шагу 4.

Шаг 4 Вычесть 1 из t. Перейти к шагу 2.

Обратите внимание, что в отличие от алгоритма Евклида, рассматриваемый алгоритм поиска НОД в описанной выше форме не будет корректно работать, если хотя бы один из его входных параметров равен нулю. Таким образом, этот пример позволяет показать, почему так важно явно определять диапазоны допустимых значений входных параметров алгоритма.

Третий способ поиска НОД должен быть вам знаком из курса средней школы.

Вычисление НОД чисел m и n "школьным" методом Шаг 1 Разложить на простые множители число m.

Шаг 2 Разложить на простые множители число n.

Шаг 3 Для простых множителей чисел m и n, найденных на шаге 1 и 2, выделить их общие делители. (Если р является общим делителем чиселm и n и встречается в их разложении на простые множители, соответственно, рm и рn раз, то при выделении нужно повторить это

min{рm, рn} раз)

Шаг 4 Вычислить произведение всех выделенных общих делителей и вернуть его в качестве результата поиска НОД двух указанных чисел.

Таким образом, для рассмотренной выше пары чисел (60,24), получим: 60 = 2 · 2 · 3 · 5 24 = 2 · 2 · 2 · 3

gcd(60,24)= 2 · 2 · 3 = 12.

Последний из рассмотренных способов поиска НОД гораздо сложне медленнее, чем алгоритм Евклида. Но даже не принимая во внимание его низкую эффективность, последний метод определения НОД, нельзя считать законным алгоритмом (по крайней мере в представленном здесь ),видетак как этапы разложения на простые множители не определены однозначно. Для их выполнения требуется иметь список простых чисел, и пока этот момент не будет прояснен, не возможно, например, написать программу, реализующую этот алгоритм.