Metody_optimizatsii

Министерство образования и науки Российской Федерации Волгоградский государственный архитектурно-строительный университет

МЕТОДЫ ОПТИМИЗАЦИИ В РЕШЕНИИ ИНЖЕНЕРНЫХ ЗАДАЧ

Лабораторный практикум

Составители О.М. Забродина, Н.А. Михайлова, А.Д. Скороходова

2-е издание, переработанное и дополненное

Волгоград 2011

УДК 004:69(075.8) ББК 32.97я73+38я73

М 545

Рецензенты:

кандидат технических наук А.В. Игнатьев, заведующий кафедрой прикладной математики и вычислительной техники Волгоградского государственного архитектурно-строительного университета (ВолгГАСУ);

кандидат технических наук Н.Н. Потапова, доцент кафедры прикладной математики и вычислительной техники ВолгГАСУ

Утверждено редакционно-издательским советом университета в качестве учебнопрактического пособия

М 545 Методы оптимизации в решении инженерных задач : лабораторный практикум [Электронный ресурс]. Элетронные текстовые и графические данные (1,24 МБ) / сост. О.М. Забродина, Н.А. Михайлова, А.Д. Скороходова ; Волгогр. гос. архит.-строит. ун-т. 2-е изд., перераб. и доп. Волгоград : ВолгГАСУ, 2011.

ISBN 978-5-98276-433-1

Учебное электронное издание комбинированного распространения:

1 CD-R диск. Системные требования: PC 486 DX-33; Microsoft Windows XP; 2-скоростной дисковод CD-ROM; Adobe Reader 6.0.

№ гос. регистрации

Официальный сайт Волгоградского государственного архитектурно-

строительногоуниверситета. Режимдоступа: http://www.vgasu.ru/publishing/on-line/

Содержит краткие теоретические сведения, необходимые для выполнения лабораторных работ. Сформулированы контрольные вопросы по темам, приведены варианты индивидуальных заданий.

1-е издание вышло в печатном тираже в 2001 г. под заглавием «Методические указания к лабораторным работам по курсу „Методы оптимизации в инженерных задачах“». Из авт. коллектива 1-го изд. выбыл А.А. Чураков, в авт. коллектив настоящего изд. вошла О.М. Забродина.

Для студентов технических специальностей очной формы обучения, изучающих дисциплину «Методы оптимизации в инженерных задачах».

УДК 004:69(075.8) ББК 32.97я73+38я73

Нелегальное копирование и использование данного продукта запрещено.

ISBN 978-5-98276-433-1

© Государственное образовательное учреждение высшего профессионального образования «Волгоградский государственный архитектурно-строительный университет», 2011

2

Оглавление
Предисловие авторов	3
Лабораторная работа 1. Графический метод решения задачи линейного
програмирования	4
Лабораторная работа 2. Решение задачи линейного программирования симплекс-
методом	10
Лабораторная работа 3. Нелинейное программирование	20
Лабораторная работа 4. Транспортная задача	27
Список рекомендуемой литературы	37

Предисловие авторов

В настоящее время теория оптимизации, успешному применению которой способствует современная компьютерная техника, вносит заметный вклад в ускорение научнотехнического прогресса. Трудно назвать такую область инженерной деятельности, где ни возникали бы задачи оптимизационного характера. Это, например, задачи определения наиболее эффективного режима работы различных технических систем, задачи на составление смесей при наименьших затратах сырья, задачи организации производства, дающего наибольшую возможную прибыль при заданных ограниченных ресурсах и др.

Курс «Методы оптимизации в решении инженерных задач» рассчитан на аудиторию, подготовленную по математике в пределах программы технического вуза. Постановка каждой задачи оптимизации включает два объекта: множество допустимых решений и целевую функцию (функционал), которую следует минимизировать или максимизировать на указанном множестве. С этой точки зрения и рассматриваются различные классы экстремальных задач, составляющие предмет изучения линейного, динамического, нелинейного, геометрического программирования, вариационного исчисления и теории оптимального управления.

Остановимся на двух направлениях: линейном и нелинейном программировании. Здесь решаются задачи оптимизации, в которых целевая функция — эта функция многих переменных, а допустимым множеством решений является подмножество евклидова пространства.

Данное пособие составлено в соответствии с программой курса и содержит описания четырех лабораторных работ по следующей схеме:

цель работы; программное обеспечение; теоретическое введение;

порядок выполнения работы; пример выполнения лабораторной работы; требования к отчету; варианты индивидуальных заданий; контрольные вопросы.

3

Лабораторная работа 1 ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ

ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Цель работы — знакомство с теорией по данной теме и применение ее в решении прикладных задач.

Теоретическое введение

Графический метод основан на геометрической интерпретации задачи линейного программирования (ЗЛП) и применяется в основном при решении задач двумерного пространства и только некоторых задач трехмерного пространства. Задачу пространства размерности больше трех измерений изобразить графически вообще невозможно.

Пусть ЗЛП задана в двумерном пространстве, т.е. ограничения содержат две переменные.

Найти минимальное значение функции

Z =C1x1 +C2 x2

(1.1)

при ограничениях

a11x1+a12x2

≤b1;

a

21

x

1

+a

x

≤b ;

(1.2)

22

2

2

..........................;

;

a

m1

x

1

+a

m2

x

≤b

2

m

x1 ≥ 0, x2 ≥ 0.

(1.3)

Допустим, что система (1.2) при условии (1.3) совместна и ее многоугольник решений ограничен. Каждое из неравенств (1.2) и (1.3) определяет полу-

плоскость с граничной прямой ai1x1 + ai2x2 =bi , где i =1,m и x1 = 0, x2 = 0.

Линейная функция (1.1) при фиксированном значении Z является уравнением

прямой: C1x1 +C2x2 = const .

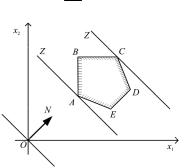
Построим многоугольник решений системы (1.2), (1.3) и график линейной функции (1.1) при Z = 0 (рис. 1.1). Тогда поставленной ЗЛП можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая C1x1 +C2x2 = const опорная и функция Z

при этом достигает минимума.	Рис. 1.1
	4

Значения Z возрастают в направлении вектора N = (C1,C2), поэтому прямую Z = 0 передвигаем параллельно самой себе в направлении вектора N.

Из рис. 1.1 видно, что прямая Z = const дважды становится опорной в точке A и C, что соответствует минимуму в точке A и максимуму в точке C. Координаты точки A (x1; x2) находим, решая систему уравнений для прямых AB и AE. Если многоугольник решений представляет неограниченную многоугольную область, то возможны два случая:

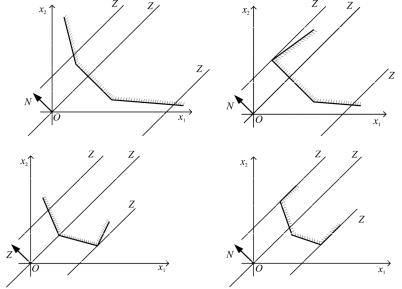
1)прямая Z = const, передвигаясь в направлении N или противоположном ему, постоянно пересекает многоугольник решений и ни в какой точке не является опорной; значит линейная функция не ограничена на многоугольнике решений как сверху, так и снизу (рис. 1.2, а);

2)прямая Z = const, передвигаясь все же становится опорной. Тогда в зависимости от вида области линейная функция может быть ограничена только сверху (рис. 1.2, б), только снизу (рис. 1.2, в) или сверху и снизу (рис. 1.2, г).

а

б

в

г

Рис. 1.2

Вообще, с помощью графического метода может быть решена ЗЛП, система ограничений которой содержит n неизвестных и m независимых уравнений, если n и m связаны соотношением n – m = 2.

Порядок выполнения лабораторной работы

1.Составить математическую модель задачи.

2.Построить многоугольник решений в системе координат x1Ox2.

3.Построить радиус-вектор и прямую Z = 0, проходящую через точку O(0; 0) перпендикулярно.

5

4.Провести прямые, параллельные прямой Z = 0, опорные по отношению

кмногоугольнику решений.

5.Найти оптимальные планы и значения Zmin и Zmax.

Примеры выполнения лабораторной работы

Пример 1. Для изготовления двух видов продукции P1 и P2 используют три вида сырья: S1, S2, S3. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, записаны в постановке ЗЛП.

х1 — количество единиц продукции P1; x2 — количество единиц продукции P2; Z — функции цели (максимальная прибыль).

1.Математическая модель задачи. Найти максимум функции Z = 50x1 +

+40x2 при ограничениях

2x1 +5x2 ≤ 20;8x1 +5x2 ≤ 40;5x1 +6x2 ≤30; x1 ≥ 0, x2 ≥ 0.

2. Построим многоугольник решений. Для этого в системе координат x1Ox2, решая неравенство на плоскости, изобразим граничные прямые (рис. 1.3):

2x		+5x	2	≤ 20 (L )
	1			1
8x1		+5x2		≤ 40 (L2 )
5x		+6x		≤30 (L	)
	1	2		3
x1	≥	0, x2	≥ 0.

Взяв какую-нибудь точку, например О (0; 0), установим, какую полу-

плоскость определяет	соответствую-
щее неравенство.
Многоугольником	решений дан-
ной задачи является	ограниченный
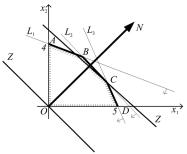
пятиугольник OABCD.	Рис. 1.3

3.Для построения прямой 50x1 + 40x2 = 0 строим радиус-вектор N(50; 40) =

=10(5; 4) и через точку О проводим прямую, перпендикулярную N.

4.Построенную Z = 0 перемещаем параллельно самой себе в направлении вектора N. Из рис. 1.3 видно, что опорной прямая Z = const становится в точке С, где Z принимает максимальное значение.

5.Точка С лежит на пересечении прямых L2 и L3. Для определения ее координат решаем систему уравнений:

{8x1 +5x2 = 40; 5x1 +6x2 =30.

Оптимальный план задачи: x1 ≈3,9; x2 ≈1,7. Подставляя x1 и x2 в Z, получаем Zmax ≈260,3.

Таким образом, чтобы получить максимальную прибыль необходимо запланировать производство 3,9 единиц продукции P1 и 1,7 продукции P2.

6

Пример 2. Графическим методом найти оптимальный план ЗЛП, при которой линейная функция Z = 2x1 − x2 + x3 −3x4 + 4x5 достигает максимально-

го значения при ограничениях

x − x +3x −18x + 2x = −4;
1		2		3		4			5
2x1		− x2	+ 4x3		−21x4		+		4x5 = 22;	(1.4)
3x		−2x	2	+8x		−43x		+11x =38;
	1				3	4			5
x j	≥	0, где j =1, 2, ... , 5.

Решение

Используя метод Жордана — Гаусса, произведем три полных исключения неизвестных х1, х2, х3. В результате приходим к системе

x				+ x	−3x = 6;
	1	x2		4		5	(1.5)
			x	+ 7x4		+10x5 = 70;
				− 4x	4	+5x = 20;
			3			5
откудаx1 = 6 − x4 +3x5;						x2 = 70 −7x4 −10x5; x3 = 20 + 4x4 −5x5.	(1.6)

Подставляя эти значения в линейную функцию и отбрасывая в системе (1.5) базисные переменные, получаем задачу, выраженную только через свободные неизвестные х4 и х5; найти максимальное значение функции Z = 6x4 +15x5 −38 при ограничениях

x	4	−3x			≤ 6;
				5			≤ 70;
7x4			+10x5
−4x			4	+5x			≤ 20;
					5
x4	≥ 0, x5				≥	0.

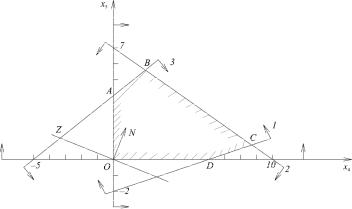
Построим многогранник решений и линейную функцию в системе координат х4Ох5 (рис. 1.4).

Рис. 1.4

7

Из рис. 1.4 заключаем, что линейная функция принимает максимальное значение в угловой точке B, которая лежит на пересечении прямых 2 и 3. В результате решения системы

{7x4 +10x5 = 70; −4x4 +5x5 = 20

находим х4 = 2, х5 = 28/5.

Максимальное значение функции Zmax = –38 + 12 + 84 = 58.

Для отыскания оптимального плана исходной задачи подставляем в формулу (1.6) найденные значения х4 и х5. Окончательно получаем х1 = 104/5;

х2 = 0; х3 = 0; х4 = 2; х5 = 28/5.

Требования к отчету

Отчет должен содержать:

1)титульный лист;

2)условие задачи;

3) чертеж с графической иллюстрацией решения задачи, пояснения

кчертежу;

4)все промежуточные окончательные вычисления;

5)вывод и анализ полученных результатов.

Варианты индивидуальных заданий

Найти минимуми максимум целевой функции при заданных ограничениях.

Z = x1

+5x2

Z = 5x1 +3x2

3x

− x

≥ 9;

6x

−5x

≥17;

Вариант 1.

1

2

≤ 50;

Вариант 2.

1

2

2x1

+3x2

x1

+2x2

≤ 34;

−x

+4x

≥19;

−4x

+9x

2

≥17;

1

2

1

x1

≥ 0, x2

≥ 0.

x1

≥

0, x2

≥ 0.

Z = 3x1 +2x2

Z = 4x1 +3x2

−4x +5x

≤ 29;

2x

− x

≥ 4;

Вариант 3.

1

2

Вариант 4.

1

2

≤ 37;

3x1

− x2

≤14;

x1

+

3x2

5x

+2x

≥ 38;

−4x

+9x

2

≥ 20;

1

2

1

x1

≥ 0, x2

≥ 0.

x1

≥

0, x2

≥ 0.

Z = 6,5x1

−7,5x3 +23,5x4

−5x5

Z = 5x1 + x2

x

+3x

+ x +4x

− x =

12;

10x

− x

2

≥ 57;

1

2

3

4

5

Вариант 6.

1

≤ 53;

Вариант 5. 2x1

− x3

+

12x4 − x5 =14;

2x1

+3x2

x

+2x

+3x

− x

= 6;

6x

−7x

≤15;

1

2

4

5

1

2

x j

≥

0, где j =1, 2, ..., 5.

x1

≥

0, x2

≥ 0.

Z = 6x1 + x2

Z = x1

+7x2

3x

− x

≥ 9;

x

+

4x

≤

53;

Вариант 7.

1

2

≤ 50;

Вариант 8.

1

2

2x1

+3x2

x1

− x2 ≤ 3;

−x

+4x

≥19;

7x

+3x

≥ 71;

1

2

1

2

x1

≥ 0, x2

≥ 0.

x1

≥

0, x2

≥ 0.

Z = x1

+8x2

78;

Z = −x1 +4x2

+2x4 − x5

−3x

+14x ≤

x −5x

+ x

= 5;

Вариант 9.

1

2

1

2

3

= 4;

5x1

−6x2

≤ 26;

Вариант 10. −x1

+ x2

+ x4

x

+4x

≥ 26;

x

+ x

+ x

=8;

1

2

1

2

5

x1

≥ 0, x2

≥ 0.

x j

≥

0, где j

=1, 2, ..., 5.

8

Z = x1 + x2

+22x

≤ 22;

2x +7x

1

2

6x3

3

6;

Вариант 11. 2x1

− x2

+

≤

−4x + x

+ x

≤

1;

1

2

3

x j ≥

0, где

j =1, 2, 3.

Z = x1

+ x2

≥53;

17x

+ x

Вариант 13.

1

2

2x1

+ x2

≤ 23;

−x

+

2x

≥1;

1

2

x1

≥

0, x2

≥ 0

Z = x1

+3x2

2x

− x

≥

4;

Вариант 15.

1

2

≤ 37;

x1

+3x2

−4x +

9x

2

≥ 20;

1

x1

≥

0, x2

≥

0.

Z = 7x1 +3x2

−6x

+9x

≤16;

Вариант 17.

1

2

≥ 48;

2x1

+11x2

2x

+ x

≤ 28;

1

2

x1 ≥

0, x2

≥ 0.

Z = x1

+ x2

≥ 53;

x

+17x

Вариант 19.

1

+2x2

2

x1

≤ 23;

2x

− x

≥1;

1

2

x1

≥

0, x2

≥ 0.

Z = −16x1

− x2

+ x3 +5x4 +5x5

2x + x

+ x =10;

1

2

3

= 6;

Вариант 21. −2x1 +

3x2

+ x4

2x

+

4x

− x

=8;

1

2

5

x j

≥ 0, где j =

1, 2,..., 5.

Z = 2x1

+ x2

+6x3

−12x4

−9x5

x

+ x

+7x −3x

−7x

=13;

1

2

3

4

5

= 20;

Вариант 23. x1

+2x2

+13x3

+2x4

−14x5

x

+3x

2

+20x

+6x

−23x

=19;

1

3

4

5

x j

≥ 0, где j =

1, 2,..., 5.

Z = 4x1

+3x2

−x

+

2x

≥ 5;

Вариант 25.

1

− x2

2

3x1

≥10;

2x

+ x

≥ 40;

1

2

x1

≥

0, x2

≥ 0.

Контрольные вопросы

Z = 3x1 + x2

−4x +5x ≤ 29;

Вариант 12. 3x1 −1 x2 ≤214;

5x1 +2x2 ≥ 38; x1 ≥ 0, x2 ≥ 0.

Z = x1

+2x3 + x5

+ x =

5;

x

+ x

+ x

+ x

1

2

3

4

5

Вариант 14. x2

+ x3

+ x4

− x5

= 2;

x

− x

+ x

=1;

3

4

5

x j

≥ 0, где j

=1, 2, ..., 5.

Z = 2x1

+3x2

10x

− x

≥ 57;

Вариант 16.

1

2

≤ 53;

2x1

+3x2

6x

−7x

2

≤15;

1

x1

≥ 0, x2 ≥ 0.

Z = 2x

+3x

−10x1

+9x

2 ≤17;

Вариант 18. 2x1

+113x2

2≥ 41;

3x

+ x

≥ 43;

1

2

x1

≥ 0, x2

≥ 0.

Z = −5x1

+ x2 − x3

3x − x

− x

= 4;

1

2

3

=1;

Вариант 20. x1

− x2

+ x3

− x4

7;

2x

+ x

2

+

2x

+ x =

1

3

5

x j

≥ 0, где j

=1, 2,..., 5.

Z = 3x1

+4x2

2x

− x

≥ 5;

Вариант 22.

1

2

≥10;

−x1

+3x2

x

+2x

≤ 40;

1

2

x1

≥ 0, x2

≥ 0.

Z = 3x1

+2x2

9x

−10x

≤17;

Вариант 24.

1

+

2

≥ 41;

13x1

2x2

x

+3x

≥ 43;

1

2

x1

≥ 0, x2

≥ 0.

1.На чем основан графический метод решения задачи линейного программирования?

2.Какие задачи линейного программирования можно решать графическим методом?

3.Каким может быть многоугольник решений?

4.Что геометрически означает каждое неравенство в системе ограничений?

9