ТВиМС / Лекции_ТВиМС / Глава 1 / Лекция 1.4. Теоремы сложения и умножения вероятностей

Тема 1.4. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

План лекции:

1. Полная группа событий и условная вероятность.

2. Формула умножения вероятностей.

3. Формула сложения вероятностей.

Список литературы:

1. Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.

2. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. - М.: Высшая школа, 2007. - 480 с.

3. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер - М: ЮНИТИ, 2002. – 543 с.

п.1. Полная группа событий и условная вероятность

Множество попарно несовместных событий называют полной группой событий, если при любом исходе случайного эксперимента непременно наступает одно из событий, входящих в это множество. Другими словами, для полной группы событий выполнены следующие условия:

• появление одного из событий данного множества в результате испытания является достоверным событием, т.е. событие ;

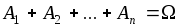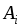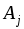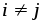• события и () попарно несовместимы и 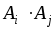– событие невозможное при любых , т.е. .

Простейшим примером полной группы событий является пара противоположных событий и .

Теорема. Сумма вероятностей событий полной группы равна единице:

.

Во многих случаях вероятности появления одних событий зависят от того, произошло другое событие или нет.

Вероятность события , вычисленная при условии, что произошло другое событие , называется условной вероятностью события и обозначается .

Вероятность каждого события в данном испытании связана с наличием известного комплекса условий. При определении условной вероятности мы полагаем, что в этот комплекс условий обязательно входит событие . Таким образом, мы имеем другой, более обременительный комплекс условий, соответствующий испытанию в новой обстановке. Вероятность появления события при этих новых условиях называется его условной вероятностью в отличие от вероятности , которая может быть названа безусловной вероятностью события .

В тех случаях, когда вероятность события рассматривается при условии, что имели место два других события и , используется условная вероятность относительно произведения событий и : .

п.2. Формула умножения вероятностей

Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

Доказательство: Предположим, что из возможных элементарных исходов событию благоприятствуют исходов, из которых исходов благоприятствуют событию . Тогда вероятность события будет , условная вероятность события относительно события будет .

Произведению событий и благоприятствуют только те исходы, которые благоприятствуют и событию , и событию одновременно, т.е. исходов. Поэтому вероятность произведения событий и .

Умножив числитель и знаменатель этой дроби на , получим:

.

Аналогично доказывается и формула .

Теорему умножения вероятностей легко обобщить на любое конечное число событий.

Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий:

.

Для доказательства этой теоремы можно использовать метод математической индукции.

п.3. Формула сложения вероятностей

Теорема: Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:

.

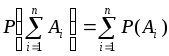Доказательство: Докажем эту теорему для случая суммы двух несовместных событий и .

Пусть событию благоприятствуют элементарных исходов, а событию – соответственно исходов. Так как события и по условию теоремы несовместны, то событию + благоприятствуют + элементарных исходов из общего числа исходов. Следовательно:

,

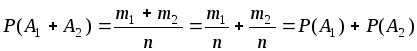где – вероятность события ;

– вероятность события.

Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

Доказательство: Событие наступит, если наступит одно из несовместных событий , , . По теореме сложения вероятностей несовместных событий:

.

Событие произойдет, если наступит одно из двух несовместных событий: , . Вновь применяя теорему сложения вероятностей несовместных событий, получаем: . Следовательно, .

Аналогично для события получаем . Откуда .

Следовательно .