ТВиМС / Лекции_ТВиМС / Глава 3 / Лекция_3.5.Статистические гипотезы

Тема 3.5. СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ

План лекции:

1. Понятие гипотезы.

2. Схема статистической проверки гипотезы.

Список литературы:

1. Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.

2. Гмурман, В.Е. Теория вероятностей и математическая статистика [Текст] / В.Е. Гмурман. - М.: Высшая школа, 2007. - 480 с.

3. Кремер, Н.Ш. Теория вероятностей и математическая статистика [Текст] / Н.Ш. Кремер - М: ЮНИТИ, 2002. – 543 с.

п.1. Понятие гипотезы.

Одна из часто встречающихся на практике задач, связанных с при­менением статистических методов, состоит в решении вопроса о том, должно ли на основании данной выборки быть принято или, напро­тив, отвергнуто некоторое предположение (гипотеза) относительно ге­неральной совокупности (случайной величины).

Например, новое лекарство испытано на определенном числе лю­дей. Можно ли сделать по данным результатам лечения обоснованный вывод о том, что новое лекарство более эффективно, чем применявшие­ся ранее методы лечения? Аналогичный вопрос логично задать, говоря о новом правиле поступления в вуз, о новом методе обучения, о пользе быстрой ходьбы, о преимуществах новой модели автомобиля или тех­нологического процесса и т. д.

Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.

Задачи статистической проверки гипотез ставятся в следующем виде: относительно некоторой генеральной совокупности высказыва­ется та или иная гипотеза Н. Из этой генеральной совокупности из­влекается выборка. Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н или принять ее.

Следует отметить, что статистическими методами гипотезу можно только опровергнуть или не опровергнуть, но не доказать. Например, для проверки утверждения (гипотеза Н) автора, что «в рукописи нет ошибок», рецензент прочел (изучил) несколько страниц рукописи.

Если он обнаружил хотя бы одну ошибку, то гипотеза Н отверга­ется, в противном случае — не отвергается, говорят, что «результат проверки с гипотезой согласуется».

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки.

Под статистической гипотезой (или просто гипотезой) понима­ют всякое высказывание (предположение) о генеральной совокупности, проверяемое по выборке.

Статистические гипотезы делятся на гипотезы о параметрах рас­пределения известного вида (это так называемые параметрические ги­потезы) и гипотезы о виде неизвестного распределения (непараметри­ческие гипотезы).

Например, статистическими являются гипотезы:

1. генеральная совокупность распределена по закону Пуассона;

2. дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.

Гипотеза «на Марсе есть жизнь» не является статистической, т.к. в ней не идёт речь ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.

Таким образом, одну из гипотез выделяют в качестве основной (или нулевой) и обозначают Но, а другую, являющуюся логическим отрицанием Н₀, т. е. противоположную Но — в качестве конкурирующей (или альтер­нативной) гипотезы и обозначают Н₁.

Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой (в ней идет речь об одном значении параметра), в противном случае - сложной.

Например, гипотеза Но, состоящая в том что математическое ожи­дание случайной величины X равно а_о, т.е. М(Х)=а_о является простой. В качестве альтернативной гипотезы можно рассматривать ги­потезу Н₁: М(Х)≠ а_о (сложная гипотеза).

Имея две гипотезы Но и Н₁, надо на основе выборки Х₁,... ,Х_п принять либо основную гипотезу Н₀, либо конкурирующую Н₁.

Правило, по которому принимается решение принять или откло­нить гипотезу Но (соответственно, отклонить или принять Н₁), назы­вается статистическим критерием К (или просто критерием) проверки гипотезы Но.

Проверку гипотез осуществляют на основании результатов выбор­ки Х₁, Х₂,..., Х_п, из которых формируют функцию выборки К_п =К(Х₁, Х₂,…, Х_n), называемой статистикой критерия.

Основной принцип проверки гипотез состоит в следующем. Мно­жество возможных значений статистики критерия К_п разбивается на два непересекающихся подмножества: критическую область S, т. е. область отклонения гипотезы Но и область принятия этой гипоте­зы. Если фактически наблюдаемое значение статистики критерия (т. е. значение критерия, вычисленное по выборке: К_набл =К(х₁,х₂,..., х_п)) попадает в критическую область S, то основная гипотеза Но отклоняет­ся и принимается альтернативная гипотеза Н₁; если же К_набл попадает в , то принимается Но, а Н₁ отклоняется.

При проверке гипотезы может быть принято неправильное реше­ние, т. е. могут быть допущены ошибки двух родов:

Ошибка первого рода состоит в том, что отвергается нулевая гипо­теза Но, когда на самом деле она верна.

Ошибка второго рода состоит в том, что отвергается альтернатив­ная гипотеза Н₁, когда она на самом деле верна.

Рассматриваемые случаи наглядно иллюстрирует следующая таб­лица.

Гипотеза Н0	Отвергается	Принимается
верна	ошибка 1-го рода	правильное решение
неверна	правильное решение	ошибка 2-го рода

Вероятность ошибки 1-го рода (обозначается через α) называется уровнем значимости критерия.

Очевидно, α = P(Н₁\Но). Чем меньше α, тем меньше вероятность отклонить верную гипотезу. Допустимую ошибку 1-го рода обычно за­дают заранее.

В одних случаях считается возможным пренебречь событиями, ве­роятность которых меньше 0,05 (α= 0,05 означает, что в среднем в 5 случаях из 100 испытаний верная гипотеза будет отвергнута), в других случаях, когда речь идет, например, о разрушении сооружений, гибе­ли судна и т. п., нельзя пренебречь обстоятельствами, которые могут появиться с вероятностью, равной 0,001.

Обычно для α используются стандартные значения: α = 0,05; 0,01; 0,005; 0,001.

Вероятность ошибки 2-го рода обозначается через β, т.е. β = Р(Н₀\Н₁).

Величину 1- β, т. е. вероятность недопущения ошибки 2-го рода (отвергнуть неверную гипотезу принять верную Н₁), называется мощностью критерия.

Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше, что, конечно, желательно (как и уменьшение α).

Последствия ошибок 1-го, 2-го рода могут быть совершенно раз­личными: в одних случаях надо минимизировать α, в другом - β. Так, применительно к производству, к торговле можно сказать, что α - риск поставщика (т.е. забраковка по выборке всей партии изделий, удовлетворяющих стандарту), β - риск потребителя (т.е. прием по выборке всей партии изделий, не удовлетворяющей стандарту); применительно к судебной системе, ошибка 1-го рода приводит к оправданию виновного, ошибка 2-го рода — осуждению невиновного. Или, например, если отвергнуто правильное решение «продолжить строительство жилого дома», то эта ошибка первого рода повлечёт материальный ущерб; если же принято неправильное решение «продолжать строительство», несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей.

Отметим, что одновременное уменьшение ошибок 1-го и 2-го рода возможно лишь при увеличении объема выборок. Поэтому обычно при заданном уровне значимости α отыскивается критерий с наибольшей мощностью.

п.2. Схема статистической проверки гипотезы.

Методика проверки гипотез сводится к следующему:

1. Располагая выборкой Х₁, Х₂,…,Х_п, формируют нулевую гипотезу Но и альтернативную Н₁.

2. В каждом конкретном случае подбирают статистику критерия К_п=К(Х₁,Х₂,..., Х_п).

3. По статистике критерия К_п и уровню значимости а определяют критическую область S (и ). Для ее отыскания достаточно найти критическую точку k_кр, т.е. границу (или квантиль), отделяющую область S от .

Границы областей определяются, соответственно, из соотношений: Р(K_п > k_кр) = а, для правосторонней критической области S; Р(K_п <k_кр) = а, для левосторонней критической обла­сти S; Р(K_п < ) = Р(K_п > ) =, для двусторонней критической области S.

Для каждого критерия имеются соответствующие таблицы, по ко­торым и находят критическую точку, удовлетворяющую приведен­ным выше соотношениям.

4. Для полученной реализации выборки 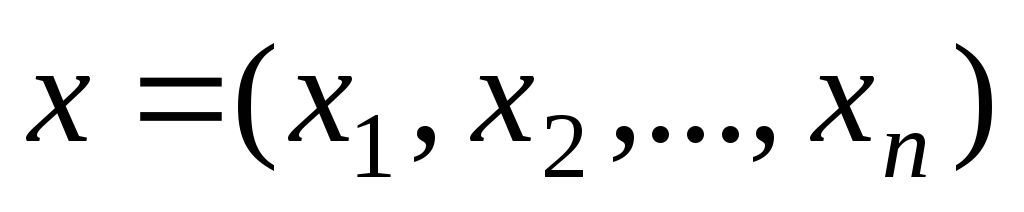подсчитывают значение критерия, т.е. К_набл =К(х₁,х2,..., х_п)= k.

5. Если 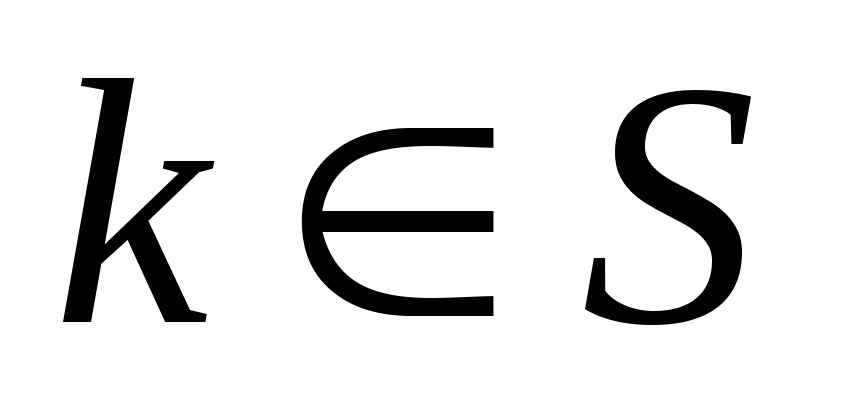(например, 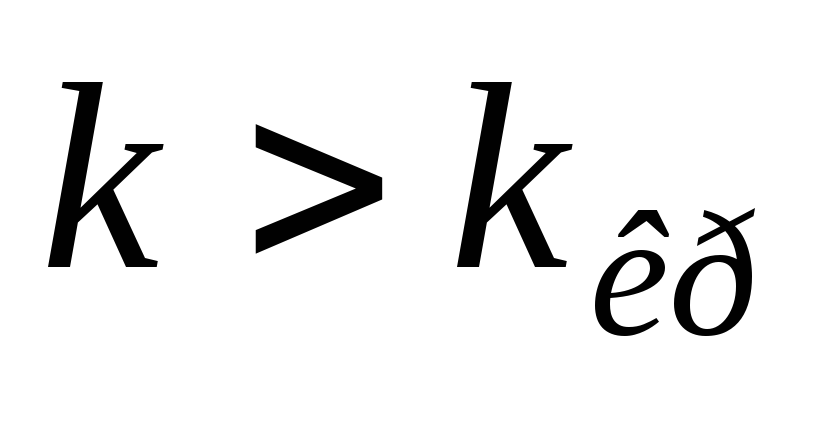для правосторонней области S), то нулевую гипотезу Н₀ отвергают, если же (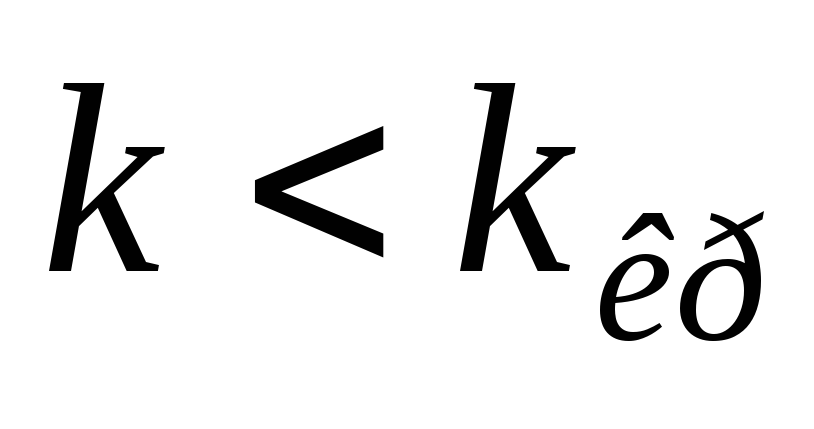), то нет оснований, чтобы отвергнуть гипотезу Но.

Во многих случаях закон распределения изучаемой случайно вели­чины неизвестен, но есть основания предположить, что он имеет вполне определенный вид: нормальный, биномиальный или какой-либо дру­гой.

Пусть необходимо проверить гипотезу Но о том, что случайная величина X под­чиняется определенному закону распределения, заданному функцией распределения F_о(х), т. е. Но: F_х(х)=F_о(х). Под альтернативной гипо­тезой Н₁ будем понимать в данном случае то, что просто не выполнена основная (т.е. Н₁: F_х(х)≠ F_о(х)).

Для проверки гипотезы о распределении случайной величины X проведем выборку, которую оформим в виде статистического ряда:

xi	x1	x2	…	Xm
ni	n1	n2	…	nm

где - объем выборки.

Требуется сделать заключение: согласуются ли результаты наблю­дений с высказанным предположением. Для этого используем специ­ально подобранную величину — критерий согласия.

Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. (Он используется для проверки согласия предполагаемого вида распреде­ления с опытными данными на основании выборки.)

Существуют различные критерии согласия: Пирсона, Колмогорова, Фишера, Смирнова и др. Критерий согласия Пирсона — наиболее часто употребляемый кри­терий для проверки простой гипотезы о законе распределения.

Рассмотрим применение критерия согласия Пирсона для проверки гипотезы о нормальном распределении исследуемой случайной величины X.

По результатам выборки подсчитывают: - эмпирическую абсолютную частоту для каждого варианта; - оценку математического ожидания; - несмещённую оценку среднего квардатического отклонения; числа в предположении нормальности случайной величины X с параметрами , ; числа - теоретические частоты, где n – объем выборки.

В качестве критерия проверки нулевой гипотезы примем случайную величину . Доказано, что при закон распределения этой случайной величины, независимо от закона распределения изучаемой величины X, стремиться к известному закону с f степенями свободы. Число f находят из равенства , где i – число частичных интервалов, r – число параметров предполагаемого распределения. В случае нормального закона r=2.

Построим правостороннюю критическую область, исходя из требования, что вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости α: . Точка по данным f и α находится по таблице критических точек распределения . На основании выборки вычисляем . Если , то нулевую гипотезу отвергают, в противном случае её можно принять.

5