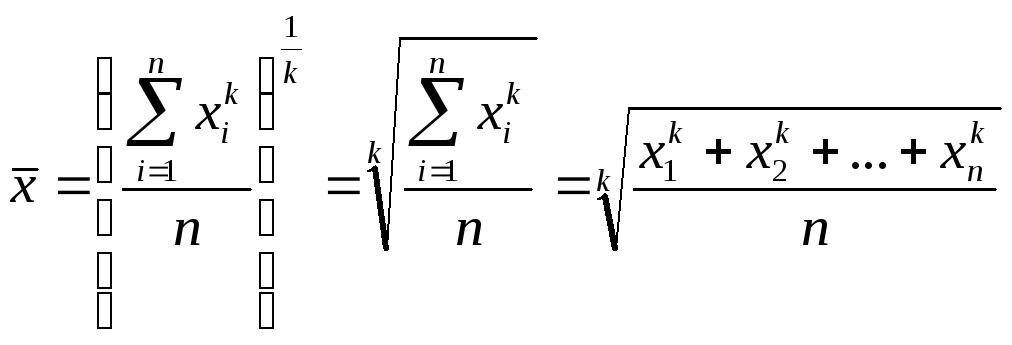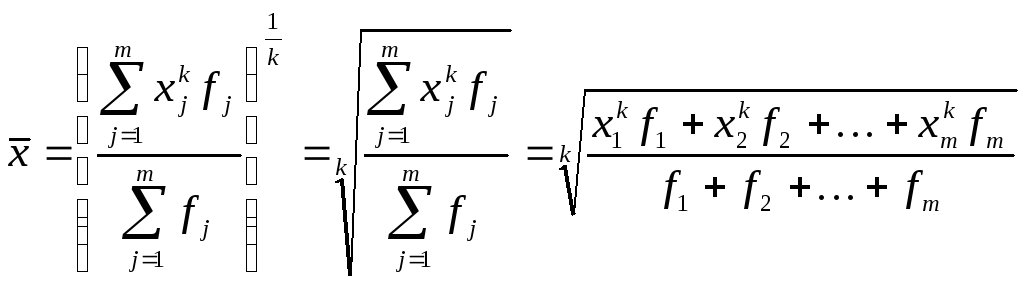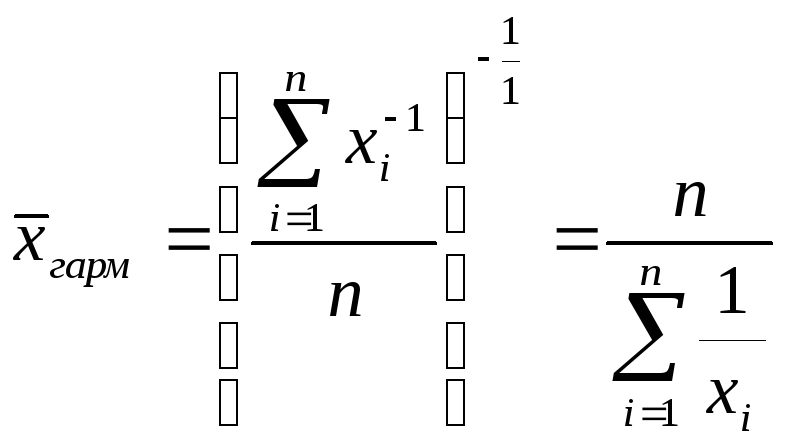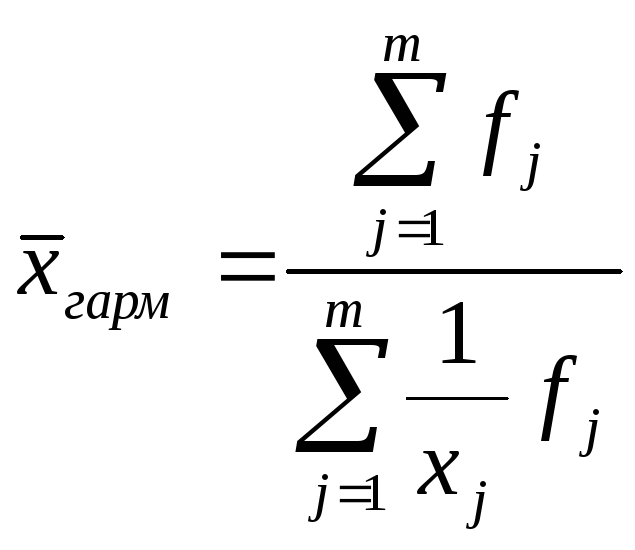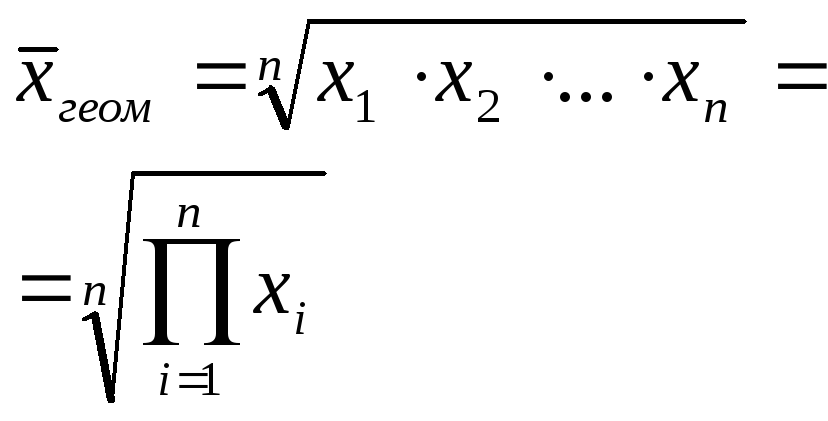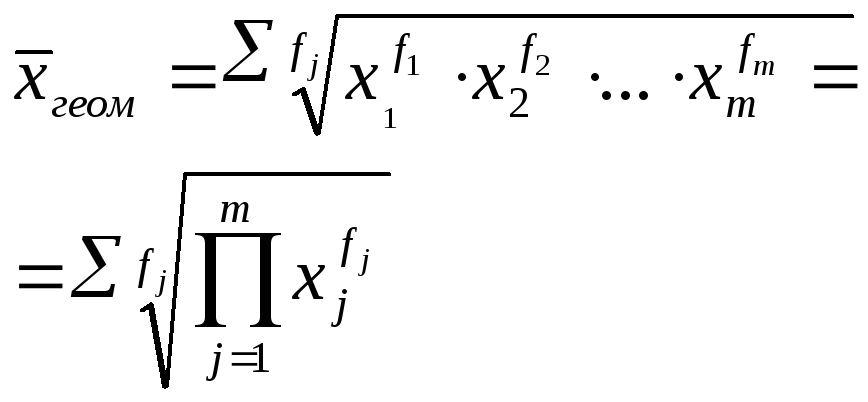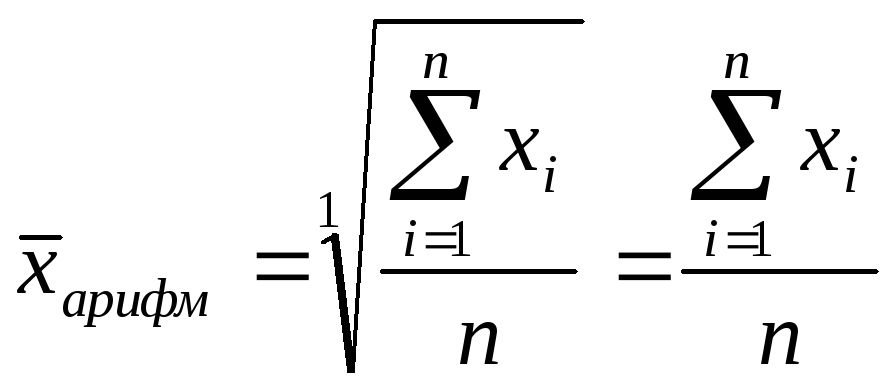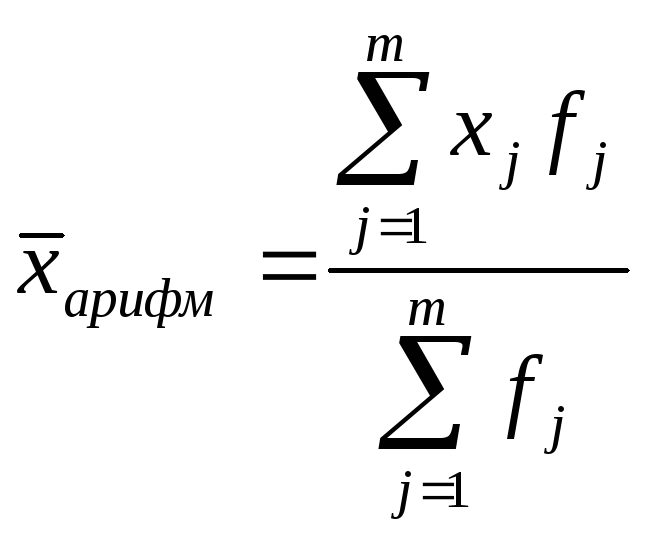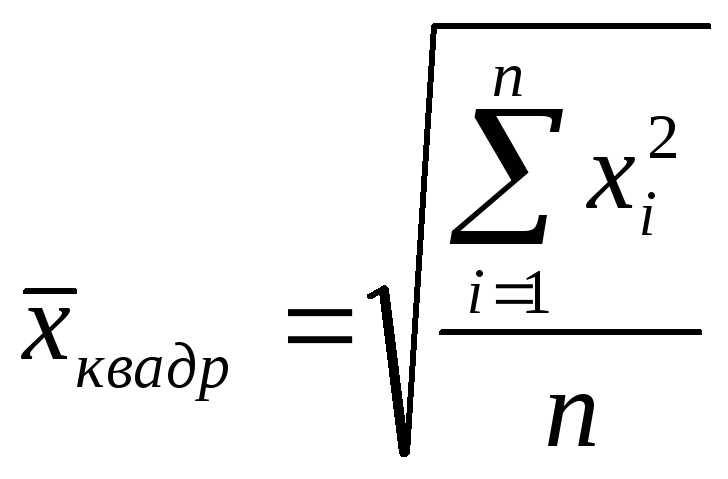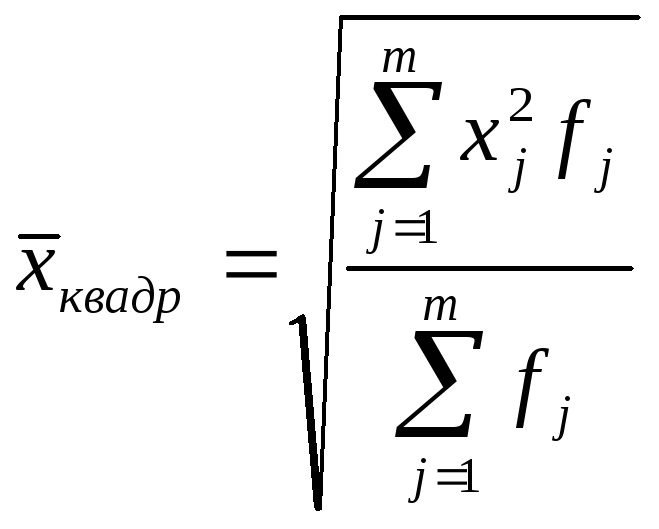65

Тема 5. Средние величины

5.1. Справочные материалы

Наиболее распространенными статистическими показателями являются статистические показатели в форме средних величин.

Средняя величина – это обобщающая мера варьирующего признака, характеризующая его уровень в расчете на единицу совокупности.

Условиями применения средних величин являются наличие качественно однородной совокупности и достаточно большой ее объем.

Определить среднюю во многих случаях можно через исходное соотношение средней или её логическую формулу:

Числитель исходного соотношения средней представляет собой определяющий показатель.

Различают две основные формы средних:

1. Степенные средние.

2. Структурные.

Общая формула степенной средней простойзаписывается следующим образом:

(5.1)

Общая формула степенной средней взвешеннойзаписывается следующим образом:

(5.2)

Изменение показателя степени k приводит в каждом отдельном случае к определенному виду средней:

Пока-затель степени	Вид средней	Формулы средней
		Простая	Взвешенная
k = -1	Средняя гармони-ческая
k= 0	Средняя геомет-рическая
k= 1	Средняя арифме-тическая
k= 2	Средняя квадра-тическая

Степенные средние, исчисленные для одной и той же совокупности, имеют различные количественные значения. Это отражено в правиле мажорантности средних: чем больше показатель степени, тем больше величина соответствующей средней:

(5.3)

Пример 5.1. Рассмотрим следующие данные о реализации продукта одного вида на трех рынках:

Рынки	Цена за ед. продукции, руб., х	Количество проданной продукции, шт., f	Выручка от продажи, руб., М
I	0,30	1000	300
II	0,35	2000	700
III	0,40	2000	800
Итого	-	5000	1800

Требуется рассчитать среднюю цену, по которой продавался товар.

Исходное соотношение средней, или ее логическая формула, выглядит следующим образом:

Пусть мы располагаем только данными о ценах на трех рынках и о количестве товара, проданного на каждом их них. При этом цены на отдельных рынках выступают в качестве вариантов, а количество проданного товара – в качестве весов. Тогда средняя цена определится по средней арифметической взвешенной, то есть

.

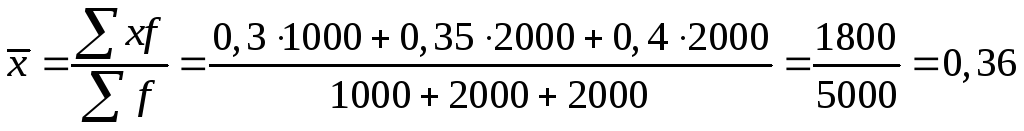Теперь предположим, что количество проданного товара неизвестно, а известны цены и выручка от продажи. В этом случае расчет следует записать в форме средней гармонической взвешенной, т.е.

.

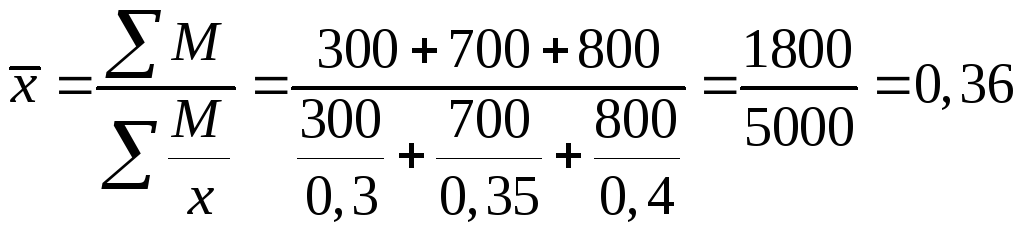Результат, как и следовало ожидать, получился тот же.

Пример 5.2. Предположим, что произведены инвестиции, приносящие ежегодный доход. Процент доходности меняется из года в год. Например, в течение 5 лет получен % дохода i₁- в первый год, i₂ во второй год, i₃ в третий год, i₄ в четвертый год, i₅- в пятый год. Доход на инвестиции начисляется один раз в год. Это значит, что после первого года сумма, равная процентному приросту i₁, добавляется к первоначальной сумме счета.

Если необходимо найти средний уровень дохода за пять лет, то можно сложить i_1, i₂, i₃, i₄, i₅ и разделить на 5. Полученная величина будет арифметической средней уровня дохода за 5 лет.

С другой стороны, если первоначальная сумма инвестиций Р, то после первого года мы имеем Р(1+i₁). В конце второго года эта сумма составит Р^.(1+i₁)(1+i₂) и т.д. После истечения пяти лет получим F=Р^.(1+i₁)(1+i₂)(1+i₃)(1+i₄)(1+i₅). Если необходимо определить средний процент дохода i, который даст сумму дохода F по истечении пяти лет, при прибавлении ежегодного накопленного прироста к сумме вклада, то это должна быть геометрическая средняя процента по вкладу. Уровень процента i есть средняя из i₁, i₂, i₃, i₄ ,i₅ в мультипликативном смысле. Это коэффициент, который находится из следующего уравнения: (i+1)⁵=(1+i₁)^.(1+i₂)^.(1+i₃)^.(1+i₄)^.(1+i₅). Решение этого уравнения находится по формуле: ,

где (i+1) геометрическая средняя из (1+i₁ ),(1+i₂),(1+i₃),(1+i₄),(1+i₅).

Например, предположим, что n = 2 года, i₁ = 0,10 и i₂ = 0,05.

Геометрическая средняя от (1+i₁) и (1+i₂) есть:

Эта средняя дает процентный рост по вкладу за два года – 0.0747, или 7,47%. Если использовать среднюю арифметическую, то x=(0,10+0,05)/2=0,075, что несколько отличается от геометрической средней. Разница в данном примере невелика, но расчет по формуле средней геометрической более верен.

Пример 5.3. Максимальный выигрыш в лотерее равен 1 000 000 рублей, а минимальный – 100 рублей. Какую величину можно считать средней между миллионом и сотней? Арифметическая средняя, равная 500 050 руб., здесь непригодна, т.к. это, как и миллион, крупный, а никак не средний выигрыш. Геометрическая средняя в этом случае дает наиболее правильный с точки зрения экономики и логики ответ:

При изучении статистической совокупности применяются такие ее характеристики, которые описывают количественно ее структуру, строение.

Квантили – это варианты, занимающие определенное место в ранжированной совокупности. К числу квантилей, наиболее часто используемых в статистическом анализе, относят перцентили, квартили, децили и медиану, которые характеризуют структуру совокупности.

Перцентиль – это значение признака в определенной позиции ранжированного ряда, мера относительной позиции варианта в ряду. Р-тый перцентиль – это значение признака, слева от которого лежит Р% вариантов ряда. Позиция Р-го перцентиля задается как (n+1)Р/100, где n – число вариантов ряда.

В статистике наиболее часто применяются квантили, которые делят ряд на четыре равные части – квартили (от латинского слова quarta - четверть).

Первый квартиль (25-й перцентиль) – это значение признака, слева от которого лежит 1/4 (или 25%) всех вариантов.

Второй квартиль – это 50 перцентиль или медиана. Медиана – значение признака, относительно которого совокупность делится на две равные по числу вариантов части.¹

Третий квартиль - это точка, слева от которой находится ¾, или 75%, вариантов ряда.

25-й перцентиль называют нижним квартилем (Q₁,), 50-й перцентиль (медиану) – средним квартилем (Q₂), 75-й перцентиль – верхним квартилем (Q₃).

В статистическом анализе также часто применяют квантили, которые делят совокупность на десять равных частей – децили. Их значения определяются соответственно как 10, 20, ..., 90 перцентили.

В общем случае квантили интервального вариационного ряда определяются по формуле:

,

(5.4)

где х _Qp(min) – нижняя граница интервала, в котором находится квантиль;

k – величина квантильного интервала (интервальная разность);

V_Qp-1 – накопленная частота или частость интервала, предшествующего квантильному;

Р – доля признаков, находящихся левее квантиля (например, для верхнего квартиля -0,25, для медианы -0,5, для седьмого дециля - 0,7);

Σf_i – сумма всех частот;

f_Qp – частота квантильного интервала.

Для расчета значения медианы в интервальном вариационном ряду вначале находят интервал, содержащий медиану. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности. Внутри медианного интервала расчет значения медианы производится по формуле:

,

(5.5)

где – нижняя граница медианного интервала;

k – величина медианного интервала;

–половина суммы всех частот (или частостей);

–накопленная частота или частость интервала, предшествующего медианному;

–частота медианного интервала.

Мода – это значение признака, наиболее часто встречающееся в совокупности. В интервальном вариационном ряду мода рассчитывается по следующей формуле:

,

(5.6)

где – нижняя граница модального интервала;

k – величина модального интервала;

–частота модального интервала;

–частота интервала, предшествующего модальному;

–частота интервала, следующего за модальным.

Пример 5.4. Правительство развивающейся страны объявило конкурс для зарубежных инвесторов на заключение контракта по строительству нового морского порта. В ответ были получены следующие предложения цены (млрд. долл.): 2, 3, 2, 4, 3, 5, 1, 1, 6, 4, 7, 2, 5, 1, 6. Построить вариационный ряд, найти среднюю арифметическую, квартили и 65-ый перцентиль.

Решение: Строим вариационный ряд

xi	1	2	3	4	5	6	7
fi	3	3	2	2	2	2	1

Рассчитаем среднюю арифметическую взвешенную:

Определим первый квартиль, или 25-ый перцентиль. Позиция этого перцентиля: (15+1)*0,25=4. Четвертое по порядку значение равно 2, т.е. Q₁=2.

Определим второй квартиль, или 50-ый перцентиль, т.е. медиану. Позиция этого перцентиля: (15+1)*0,5=8. Восьмое по порядку значение равно 3, т.е. Q₂=Ме=3.

Определим третий квартиль, или 75-ый перцентиль. Позиция этого перцентиля: (15+1)*0,75=12. Двенадцатое значение признака равно 5, т.е. Q₃=5.

Позиция 65-го перцентиля: (15+1)*0,65=10,4. Десятый по порядку вариант равен 4, а одиннадцатый равен 5. Значение 65-го перцентиля находится в точке, которая делит расстояние десятым и одиннадцатым признаком в отношении 0,4 к 1. Следовательно, Р₆₅=4+0,4(5-4)=4,4.²

Среднюю арифметическую, медиану и моду часто называют мерами центральной тенденции.

Что характеризуют эти три меры и каковы их достоинства и недостатки? Средняя суммирует всю информацию и является центром массы. Медиана – это значение признака в центре набора данных. Одна половина значений признака лежит левее этой точки, другая – правее. Точное местонахождение любой точки не существенно при определении медианы; важно только ее положение относительно центрального значения, т.е. медиана устойчива по отношению к крайним значениям ряда. Средняя арифметическая, напротив, чувствительна к положению крайних значений ряда. Тем не менее средняя арифметическая имеет существенные преимущества перед другими мерами центральной тенденции. Средняя арифметическая основывается на информации, содержащей все значения ряда, в то время как медиана базируется только на значении, лежащем «в середине ряда». Если же необходимо предотвратить влияние нескольких наблюдений, лежащих далеко от центра ряда, то надо использовать и медиану. Например, если изучается распределение доходов и имеет место высокая степень неравенства, т.е. присутствует некоторое число единиц наблюдения как с очень высокими, так и с очень низкими доходами, то логичнее рассчитывать не средний доход, а медианный. В такой ситуации он более адекватно отразит типичное значение дохода.

Мода не так популярна в статистическом анализе, как средняя арифметическая и медиана. В одном ряду может быть несколько мод. Моде отдается предпочтение при изучении цен на рынке, спроса населения на отдельные продукты питания, одежду и обувь определенных размеров. Если средняя арифметическая близка к моде и медиане, то она типична. Вычисление моды особенно существенно в несимметричных рядах, когда она сильно отличается от медианы и средней арифметической.