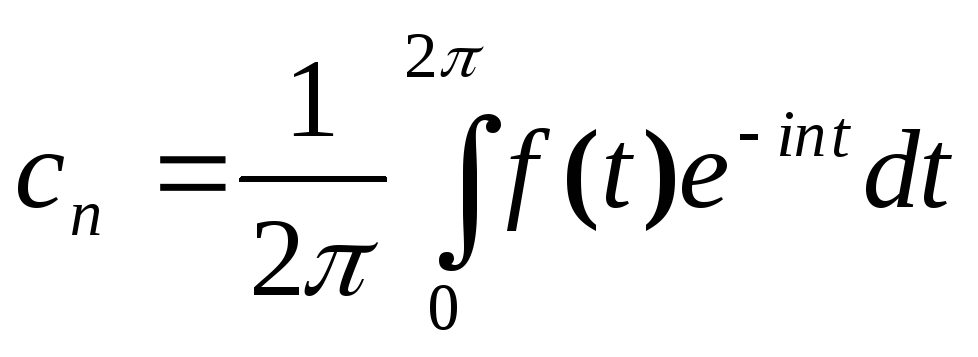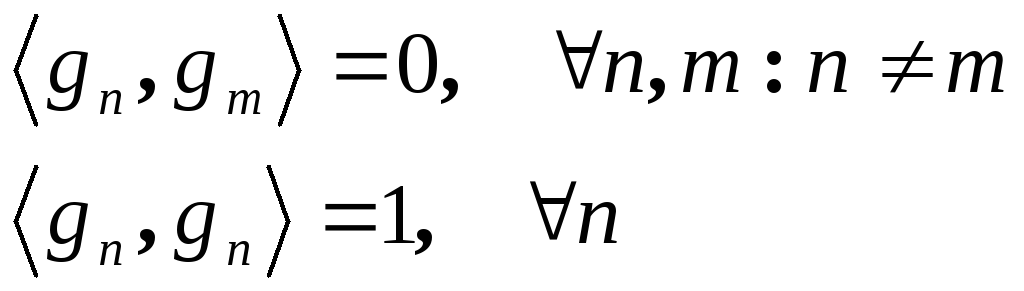Кусайкин Д.В / ЦОС заочникам / Лабораторная работа _3

Лабораторная работа №3

Изучение преобразования Фурье, частотных характеристик chirp сигналов.

Цель работы: Изучить основы спектрального представления сигналов.

Содержание отчета:

1. Выражение, представляющее разложение периодического сигнала на гармонические составляющие

2. Выражение интеграла Фурье

3. Графики, получающиеся по ходу выполнения работы

1 Теоретическая справка.

1.1 Преобразование Фурье и ряд Фурье

Ряд Фурье. Можно показать, что такая 2-периодическая функция может быть представлена как суперпозиция целочисленных растяжения базисной функции , т.е.

(0)

где

(0)

Компоненты образуют ортонормированную систему функций, т.е.

(0)

Ряд (1) называется рядом Фурье. Ряд Фурье применим для разложения периодических функций.

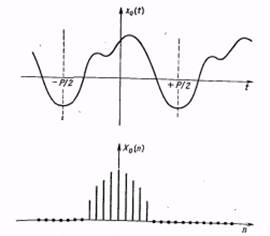
Рисунок 1.1 Периодическая функция x0(t) с ограниченной полосой частот и ее спектр

Для иллюстрации применения разложения в ряд Фурье рассмотрим формирование меандра.

Меандр – это последовательность прямоугольных импульсов со скважностью, равной двум¹.

В спектре меандра присутствуют только нечетные гармоники.

(0)

Гармоники образующие меандр имеют амплитуду обратно пропорциональную номеру соответствующей гармоники.

Интеграл Фурье. Аналитический спектр аналогового непериодического сигнала может быть получен с помощью преобразования Фурье (интеграл Фурье):

Спектр одного прямоугольного импульса с параметрами A , и равен:

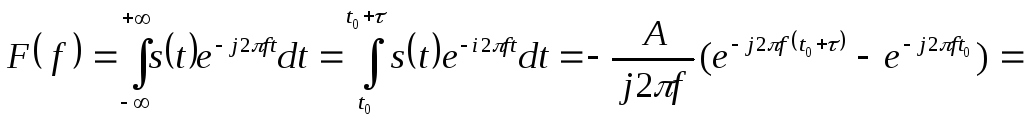
Отсюда амплитудный спектр прямоугольного импульса

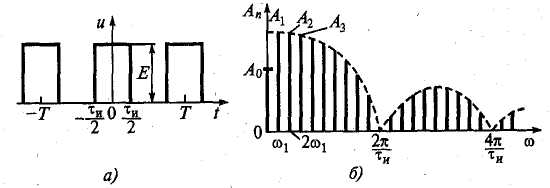
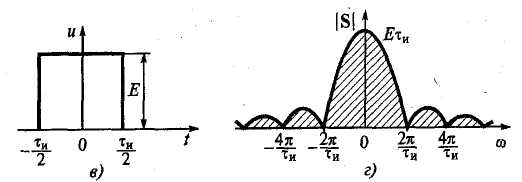
Рисунок 1.2 Прямоугольные импульсы:

а, б— периодическая последовательность и ее спектр;

в, г — одиночный импульс и его спектральная плотность

1.2 Явление Гиббса.

Чаще всего с изменением частотных характеристик функций приходится сталкиваться при усечении операторов фильтров. На примере усечения операторов и рассмотрим характер происходящих изменений.

При расчетах фильтров, как правило, задается определенная передаточная характеристика H(w) фильтра, и по ней производится расчет оператора фильтра h(n), количество членов которого может оказаться очень большим, в пределе - бесконечным. Усечение может рассматриваться, как результат умножения функции оператора фильтра на селектирующее весовое окно длиной 2N+1. В простейшем случае это окно представляет собой П-образную селектирующую функцию:

h_n = h(n) П_N(n), П_N(n) = 1 при |n| £ N, П_N(n) = 0 при |n| > N.

Функция h(n) оператора фильтра обуславливает определенную частотную передаточную характеристику фильтра H(w). Полному оператору h(n) соответствует исходная частотная характеристика H(w):

H(w) =h(n) exp(-jwn). (3.1.1)

Сущность явления Гиббса. Усеченной функции h_n во временном окне селекции П_N(n) в частотном пространстве соответствует спектральная функция, которая в определенной степени должна отличаться от функции H(w). Очевидно, что при усечении ряда Фурье (3.1.1), до конечного числа членов ±N мы будем иметь усеченный ряд Фурье:

H_N(w) =h(n) exp(-jwn), (3.1.2)

при этом сходимость суммы остающихся членов ряда H_N(w) к исходной передаточной функции H(w) ухудшается, и происходит отклонение частотной характеристики фильтра от первоначально заданной в тем большей степени, чем меньше значение N. Особенно ярко это проявляется на крутых перепадах (разрывах, скачках) в передаточных функциях:

- крутизна перепадов "размывается", т.к. она не может быть больше, чем крутизна (в нулевой точке) последней сохраненной гармоники ряда (3.1.2);

- по обе стороны "размытых" перепадов появляются выбросы и затухающие осцилляции с частотой, близкой к частоте первого отброшенного члена ряда (3.1.1).

Эти эффекты (см. рис. 3.1.2) при усечении рядов Фурье получили название явления Гиббса.

1.3 Дискретное преобразование Фурье (ДПФ)

Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций).

Прямое преобразование:

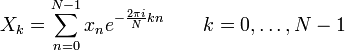
Обратное преобразование:

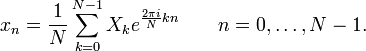
N – количество значений сигнала, измеренных за период, а также количество компонент разложения;

— измеренные значения сигнала (в дискретных временных точках с номерами , которые являются входными данными для прямого преобразования и выходными для обратного.

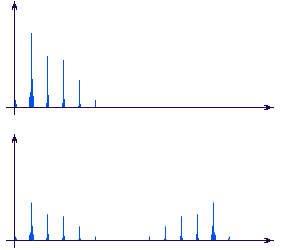
Рисунок 1.3

На этом рисунке сверху показан ожидаемый спектр сигнала, полученный с помощью непрерывного преобразования Фурье, а снизу - полученный на компьютере с помощью дискретного преобразования Фурье. Нижний спектр искажен зеркальным эффектом (рис. 1.4).

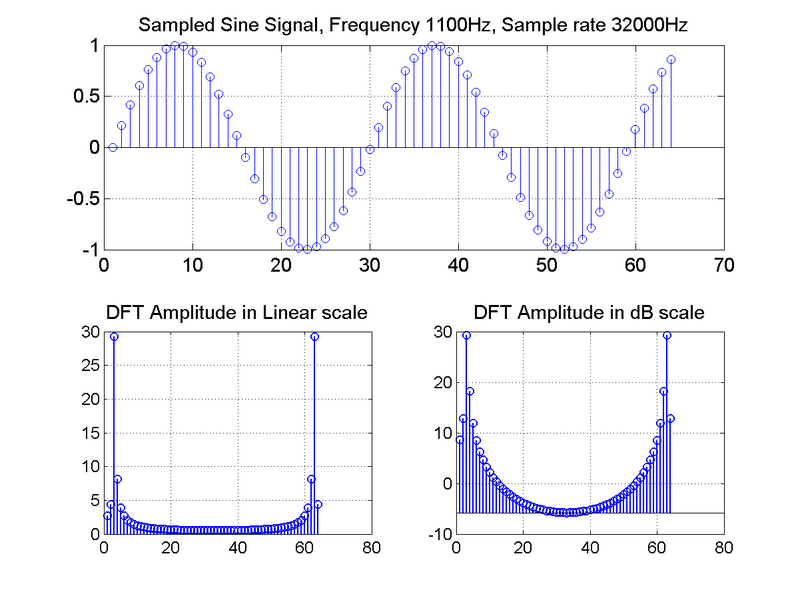
Рисунок 1.4 Дискретный сигнал и его ДПФ

Выполнение работы

1. Представление сигнала гармоническими составляющими

N=16;

t=-1:0.01:1;

A=1;

T=1;

nh=(1:N)*2-1;

harmonics=cos(2*pi*nh'*t/T);

Am=2/pi./nh;

Am(2:2:end)=-Am(2:2:end);

s1=harmonics.*repmat(Am',1,length(t));

s2=cumsum(s1);

for k=1:N

subplot(4,4,k)

plot(t, s2(k,:))

end

Зарисовать 1 строку таблицы графиков. Сделайте вывод о сходимости ряда Фурье к рассматриваемому сигналу.

2. Явление Гиббса

% Приближение сигнала

T=20;

w0 = 2*pi/T;

t = -1.5*T:T/1000:1.5*T;

N = input('Number of harmonics:');

c0 = 0;

x = c0*ones(1,length(t)); % dc component

for n=1:N,

cn = j./n/pi.*(cos(n*pi)-1);

c_n = conj(cn);

x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);

end

figure(3);

plot(t,x);

grid

title(['N = ',num2str(N)])

Промоделировать приближение сигнала при 20,60 и 100 гармониках. Зарисовать «верхушку» импульса при 20 гармониках.

3) Cинтез периодического сигнала с использованием пакета Simulink. Соберите схему, указанную на рисунке ниже и зарисуйте осциллограммы. Задайте для каждого генератора свою частоту сигнала (произвольно).

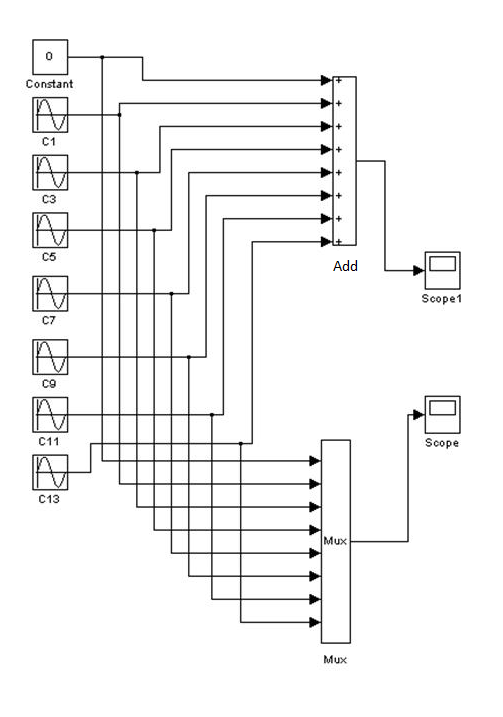
Рис. 1 Вид S - модели Фурье-синтеза сигнала

4) Спектр непериодических сигналов

N=128;

A1=0.5;

t1= 0 ;

tau1= 0.0625;

f =(0.01:0.01:N);

%p1(t)

Fp1=(A1*sin(pi*f*tau1)./(pi*f)).*exp(-j*pi*f*(2*t1+tau1));

%abs(Fp1(1:3000))/abs(Fp1(1))

plot(-1.4:0.001:1.2,rectpuls(-1.4:0.001:1.2,tau1),1,2)

figure

plot(f(1:4000),abs(Fp1(1:4000))),grid

title('Amplitude spectr of p1(t)');

Изменяя длительность импульса (параметр tau1) сделайте вывод о зависимости ширины спектра сигнала от длительности сигнала во времени.

Зарисуйте получившиеся графики и подпишите их. Сделайте вывод

5) Спектры chirp сигналов.

Соберите приведенную схему (рисунок 2). Изменяя по своему усмотрению параметры генератора сигналов и chirp генератора добейтесь наиболее наглядной картины графиков сигналов. (обязательно рассмотреть все виды параметра frequency sweep (закон изменения частоты)в блоке chirp). Зарисовать сигналы и проанализировать их спектры. Параметры анализатора спектра задавать в соответствии с рисунком 3.

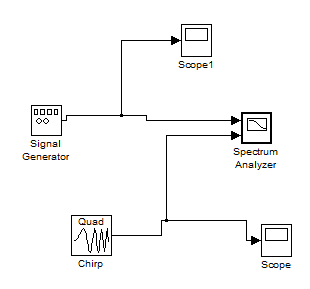
Рисунок 2

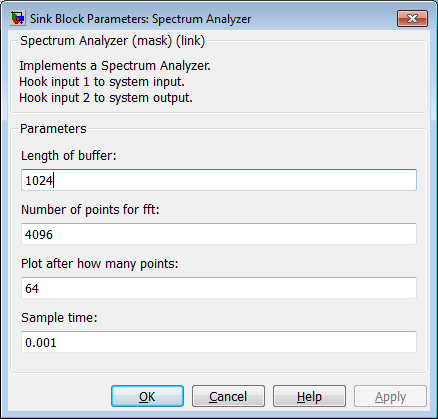
Рисунок 3

6) Дискретное преобразование Фурье

Основное назначение преобразования Фурье - выделить частоты регулярных составляющих сигнала, зашумленного помехами. Рассмотрим данные, поступающие с частотой 1000 Гц. Сформируем сигнал, содержащий регулярные составляющие с частотами 50 Гц и 120 Гц и случайную аддитивную компоненту с нулевым средним.

По временной осциллограмме нельзя сказать какие частоты содержит принятый сигнал. В этом случае помогает разложение дискретного сигнала в ДПФ.

t = 0:0.001:0.6;

x = sin(2 * pi * 50 * t) + sin(2 * pi * 120 * t);

y = x + 2 * randn(size(t));

plot(y(1:50)), grid

Y = fft(y, 512);

Pyy = Y.*conj(Y)/512;

f = 1000 * (0:255)/512;

figure(2), plot(f, Pyy(1:256)), grid

Y = fftshift(Y);

Pyy = Y.*conj(Y)/512;

figure, plot(1000/512*(-256:255),Pyy), grid

Контрольные вопросы:

1. Как можно представить в частотной области периодический сигнал?

2. Как можно представить в частотной области непериодический сигнал?

3. Что такое явление Гиббса?

4. Какая связь между длительностью сигнала во времени и спектром сигнала?

5. Что такое chirp сигнал?

6. Какие существуют виды преобразований Фурье?

1 Скважность – отношение периода к длительности импульса