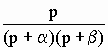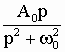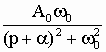Билет №30

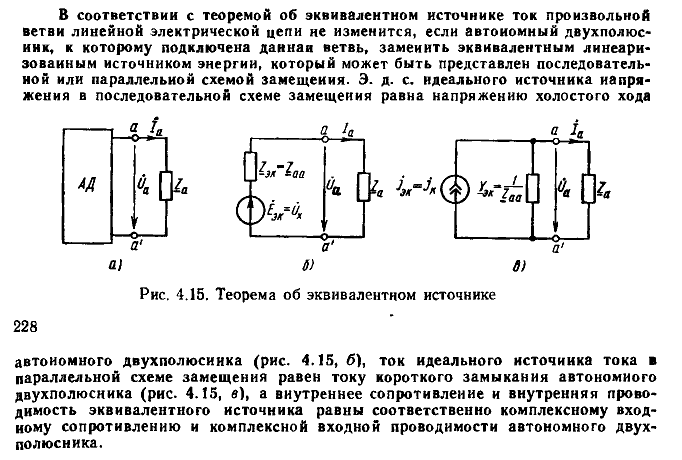
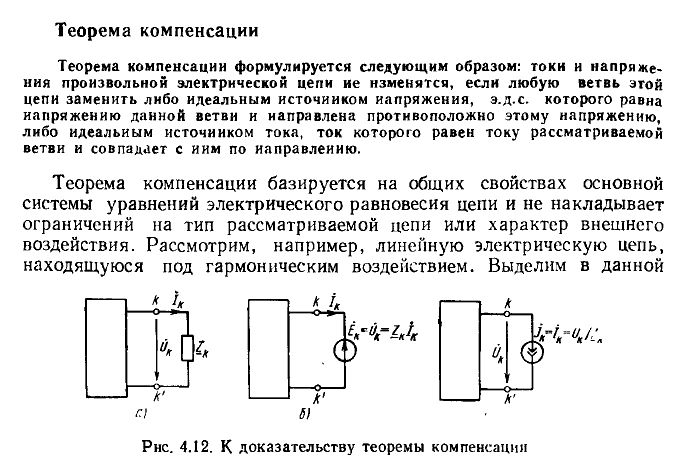
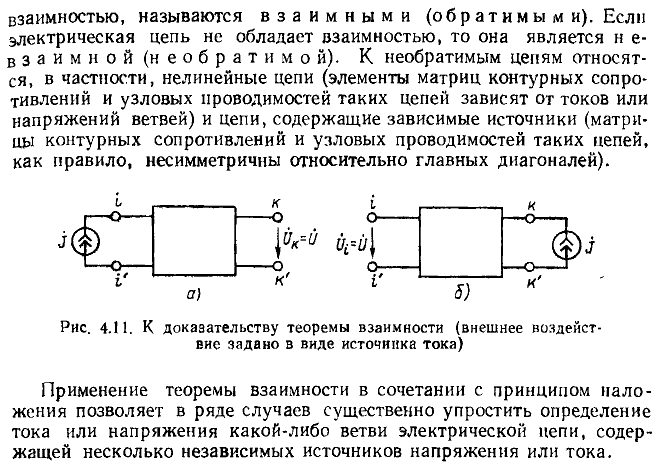
Основные теоремы линейных цепей: теорема обратимости, теорема компенсации, теоремы об эквивалентном источнике.

Анализ переходных процессов операторным методом

В основе операторного метода лежит преобразование Лапласа и операционное исчисление, известные из курса высшей математики. Операторный метод позволяет производить анализ переходных процессов при воздействии сигналов любой формы и не требует определения постоянных интегрирования, что существенно упрощает анализ электрических цепей, порядок которых выше чем первый.

 

3.1 Преобразование Лапласа и его основные свойства.

 

Пусть f(t) - функция действительного переменного t, которая удовлетворяет следующим условиям:

  f(t) тождественно равно нулю при t<0;

  f(t) - однозначная кусочно-непрерывная функция с конечным числом разрывов первого рода;

  При t  функция f(t) растет не быстрее чем экспонента, т.е. 

, где M₀ и S₀ - положительные действительные числа.

Указанным условиям удовлетворяют практически все функции времени, используемые в электротехнических задачах. При этих условиях существует интегральное преобразование Лапласа от функции f(t):

,

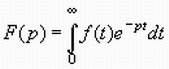(3.1)

где f(t) - оригинал; F(p) - изображение исходной функции;  - комплексная переменная.

Таким образом преобразование Лапласа устанавливает взаимно однозначное соответствие между исходной функцией времени f(t) и другой функцией другой (комплексной) переменной F(p). Для обозначения того, что эта пара функций связаны преобразованием Лапласа (3.1) будем использовать краткую запись  или .

Рассмотрим некоторые свойства преобразования Лапласа, необходимые для дальнейшего рассмотрения операторного метода. Доказательство их проводится в соответствующем курсе математики.

1. Линейность преобразования: изображение суммы функций равно сумме изображений слагаемых.

Если  и , то

,

(3.2)

где к₁ и к₂ - вещественные числа.

Это свойство следует непосредственно из определения преобразования (3.1) и может быть распространено на произвольное число слагаемых.

2. Дифференцирование оригинала.

Если , то ,

(3.3)

где  - производная, f(0) - начальное значение исходной функции.

При нулевых начальных условиях (f(0) = 0) имеем простое соотношение: .

3. Интегрирование оригинала.

Если , то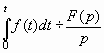 

(3.4)

4. Теорема запаздывания.

Если , то 

(3.5)

5. Произведение изображений.

Если  и , то

(3.6)

Интегралы в правой части называют сверткой функций. Произведение изображений соответствует свертке оригиналов. Свертка двух функций соответствует произведению их изображений.

 

3.2. Изображение простейших функций.

1. Единичная импульсная функция , где А₀ - вещественное число. Изображение по Лапласу:

.

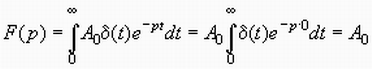Поскольку  отлична от нуля только для момента t = 0, то под знаком интеграла вся функция также будет отлична от нуля только для этого момента времени. Учитывая, что экспонента в нулевой степени и интеграл от  равны единице , получим приведенный результат.

2. Экспоненциальная функция .

3. Изображение ступенчатой функции (постоянной величины) . Заметим, что данную функцию можно получить из экспоненциальной при a = 0. Поэтому искомое изображение по Лапласу: . Этот результат можно получить из предыдущего примера при .

Существуют довольно обширные справочные таблицы, которые содержат пары оригинал - изображение для различных функций времени. Небольшая справочная таблица такого рода приведена ниже. В нее включены, кроме функций, рассмотренных выше в примерах, еще несколько пар оригинал - изображение, которые часто встречаются в задачах анализа переходных процессов. Заметим, что с помощью таблицы можно найти не только прямое (по f(t) определить F(p)), но и обратное преобразование (по F(p) определить f(t)).

 

 

Таблица 3.1.

	Оригинал	Изображение
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.