2 курс 1 часть / отц / экзамен / шпоры / Билет 17

Билет 17

1. 1. Комплексная частотная характеристика простого параллельного колебательного контура, особенности амплитудно-частотной и фазо-частотной характеристики. Резонансная частота, добротность, полоса пропускания, связь между ними.

Частотные характеристики параллельного колебательного контура

Простейший параллельный колебательный контур с потерями в ветвях R₁ и R₂ имеет вид, изображенный на рис. 4.13. Комплексная входная проводимость такого контура

, (4.53)

где Y₁ = G₁—jВ₁; Y₂ = G₂—jВ₂ — комплексные проводимости ветвей с индуктивностью и емкостью соответственно. Проводимости G₁, G₂, B₁, B₂ можно найти из формул преобразования (3.57):

(4.54)

где ; .

Из условия резонанса токов имеем: = arctg(B/G) = 0. Отсюда следует:

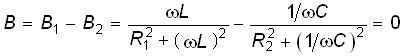. (4.55)

Решив (4.55) относительно , получим уравнение резонансной частоты:

. (4.56)

Из уравнения (4.56) следует, что резонанс в параллельном контуре возможен лишь в случае неотрицательности подкоренного выражения (т. е. при R₁ < и R₂ < , или R₁ > и R₂ > ).

Реактивные составляющие токов в ветвях при резонансе равны друг другу:

. (4.57)

При этом ток в неразветвленной части цепи определяется из уравнения

, (4.58)

где активное сопротивление R_0э, называют эквивалентным резонансным сопротивлением параллельного контура. Как следует из уравнения (4.58), входной ток контура совпадает по фазе с приложенным напряжением. Величину R_0э можно найти из условия резонанса токов. Так как при резонансе токов В = 0, то согласно (4.53) и (4.54) полная эквивалентная проводимость контура

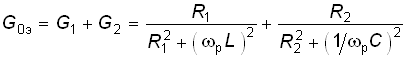. (4.59)

Подставив значение _p из (4.56) в (4.59) получим:

, (4.60)

откуда

. (4.61)

Наибольший теоретический и практический интерес представляют резонанс токов в контурах без потерь и с малыми потерями.

Контур без потерь. Для контура без потерь (R₁ = R₂ = 0) уравнение резонансной частоты (4.56) принимает вид

, (4.62)

т. е. совпадает с выражением (4.21) для последовательного контура. Эквивалентное сопротивление контура без потерь R_0э = и входной ток равен нулю, а добротность обращается в бесконечность. Комплексы действующих значений токов в ветвях

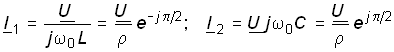, (4.63)

т. е. ток в индуктивности отстает от приложенного напряжения на /2, а в емкости опережает на /2. На рис. 4.14, а изображена векторная диаграмма токов для этого случая при U = Ue^j0 = U.

Рис. 4.14

Сумма энергий электрического и магнитного полей для параллельного контура без потерь, как и для последовательного контура остается неизменной, т. е. энергетические процессы протекают аналогично процессам в последовательном контуре.

Частотные зависимости характеристик параллельного контура от частоты имеют вид

(4.64)

На рис. 4.15 изображены графики зависимостей (4.64). Как следует из рисунка, при < ₀ входное сопротивление контура носит индуктивный, а при > ₀ емкостный характер, причем вследствие отсутствия потерь при переходе через = ₀ ФЧХ контура изменяется скачком от — /2 до /2, а входное реактивное сопротивление контура претерпевает разрыв (|Х| = ). Частотная зависимость входного тока определяется уравнением

, (4.65)

т. е. является зеркальным отображением модуля реактивной проводимости |В( )| (на рис. 4.15 показано штриховой линией).

Контур с малыми потерями (R₁ ; R₂ p). Резонансная частота для этого случая будет приближенно совпадать с частотой ₀. Для контура с малыми потерями можно принять, что ²  R₁R₂, тогда

, (4.66)

где R = R₁ + R₂. Ток в неразветвленной части цепи

, (4.67)

а комплексные значения токов в ветвях

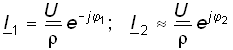, (4.68)

где

,

т. е. действующие значения токов в ветвях

. (4.69)

Из уравнений (4.67) и (4.69) следует, что отношение токов в ветвях к току в неразветвленной части цепи равно добротности контура:

, (4.70)

т. е. ток в реактивных элементах L и С при резонансе в Q раз больше тока на входе контура (отсюда термин “резонанс токов”). На рис. 4.14, б изображена векторная диаграмма токов для этого случая. В контуре с потерями сумма энергий электрического и магнитного полей не остается постоянной с течением времени.

Рис. 4.15

Интересен случай R₁ = R₂ = . Как следует из уравнения (4.56), для _р получаем неопределенность, при этом входное сопротивление контура имеет чисто резистивный характер на любой частоте (случай безразличного резонанса).

Рассмотрим частотные характеристики контура с малыми потерями. Комплексное эквивалентное сопротивление контура можно определить уравнением

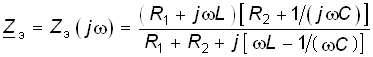. (4.71)

В режиме малых расстроек в цепи с незначительными потерями с учетом малости потерь (R₁ L и R₂ 1/ C) уравнение (4.71) можно переписать в такой форме:

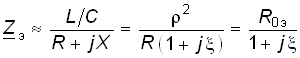. (4.72)

Выделяя в (4.72) активную R_э и реактивную Х_э составляющие, получаем уравнения частотных характеристик:

. (4.73)

На рис. 4.16, а изображены нормированные относительно R_0эчастотные характеристики R_э/R_0э, X_э/R_0э, и Z_э/R_0э как функции обобщенной расстройки . Фазочастотная характеристика цепи определится уравнением (рис. 4.16, б):

. (4.74)

Рис. 4.16

Анализ полученных зависимостей показывает, что по своему виду частотные характеристики контура с потерями существенно отличаются от характеристик контура без потерь. Это отличие касается прежде всего зависимости реактивного сопротивления контура от частоты: для контура с потерями при резонансе оно оказывается равным нулю (см. рис. 4.16, а), а в контуре без потерь терпит разрыв (см. рис. 4.15).

Зависимость комплексного входного тока от частоты определяется из уравнения

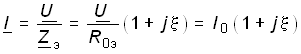, (4.75)

т. е. при резонансе ( = 0) ток принимает минимальное значение, определяемое формулой (4.58) (рис. 4.16, в).

Частотная зависимость токов I₁( ) и I₂( ) в ветвях определяется согласно закону Ома:

,

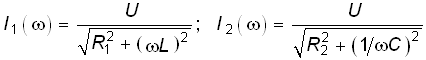т. е. ток I₁ с увеличением частоты уменьшается, а I₂ растет, причем в пределе I₁( ) = 0; I₂( ) = U/R₂.

Комплексная передаточная функция по току в ветвях с L и С параллельного колебательного контура определяется в соответствии с (4.2):

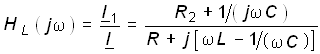; (4.76)

. (4.77)

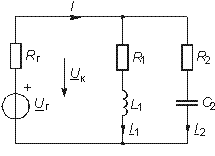
Рис. 4.17

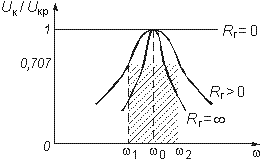
Рис. 4.18

Отсюда получаем АЧХ и ФЧХ КПФ по току для контура с малыми потерями:

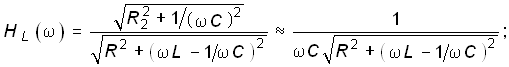(4.78)

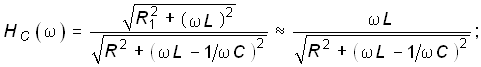(4.79)

(4.80)

(4.81)

В контуре с малыми потерями при резонансе АЧХ принимает значения:

. (4.82)

Сравнение формул (4.32)—(4.38) с формулами (4.78)—(4.81) показывает, что КПФ по току параллельного контура дуально соответствует КПФ по напряжению для последовательного контура.

Рассмотрим, как влияет на резонансные свойства параллельного контура подключение его к источнику с задающим напряжением U_г и внутренним сопротивлением R_г. При этом выходное напряжение снимается с контура (рис. 4.17). Нетрудно видеть, что комплексное напряжение на контуре

, (4.83)

где Z_э определяется формулой (4.71). При резонансе токов

. (4.84)

Определим отношение U_к/U_кр с учетом (4.72), (4.83), (4.84);

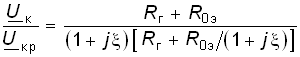. (4.85)

Введем понятие эквивалентной добротности контура

. (4.86)

Тогда после несложных преобразований формулы (4.85) с учетом (4.44) и (4.86) получаем

. (4.87)

Из (4.87) нетрудно получить АЧХ и ФЧХ относительно напряжения на контуре, нормированного к напряжению U_кр,

; (4.88)

. (4.89)

На рис. 4.18 показан характер этих зависимостей при различных сопротивлениях R_г источника.

Полоса пропускания параллельного контура определяется как полоса частот, на границе которой напряжение на контуре уменьшается в раз относительно U_кр (см. рис. 4.18):

.

Отсюда получаем уравнение граничных частот полосы пропускания:

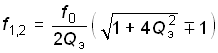. (4.90)

При этом абсолютная f_a и относительная f₀ полосы пропускания будут равны:

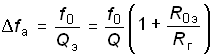, (4.91)

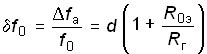. (4.92)

Сравнение уравнений (4.50) с уравнениями (4.91) и (4.92) показывает, что параллельный контур в общем случае имеет более широкую полосу пропускания, чем последовательный с такой же добротностью. И только при R_г = (см. рис. 4.18) их полосы пропускания равны.

Таким образом, для улучшения избирательных свойств параллельного контура его необходимо возбуждать источником тока. Из уравнения (4.84) также следует, что параллельный контур нельзя использовать для усиления напряжения, если использовать независимый источник, так как при этом U_кp < U_г.

Рис. 4.19

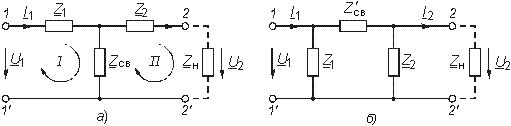
Рис. 4.20

Поэтому для усиления напряжения и получения высокой добротности параллельного контура используют активные цепи с зависимыми источниками тока. На рис. 4.19 приведен пример подобной схемы на базе полевого транзистора и его эквивалентная схема замещения.

2. Интеграл Дюамеля

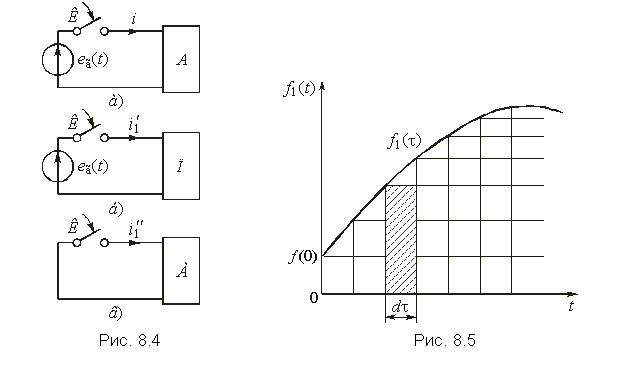
Интеграл Дюамеля может быть получен, если аппроксимиро­вать приложенное воздействие f₁(t) с помощью единичных функ­ций, сдвинутых относительно друг друга на время Dt (рис. 8.2).

Реакция цепи на каждое ступенчатое воздействие определится как

                               

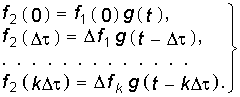
Результирующая реакция цепи на систему ступенчатых воздей­ствий найдется, исходя из принципа наложения:

    

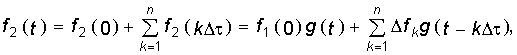
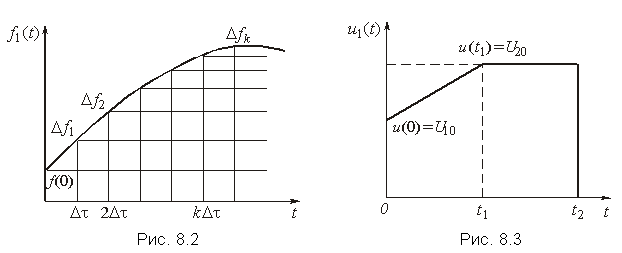где п — число аппроксимирующих участков, на которые разбит ин­тервал 0 ... t. Домножив и разделив выражение, стоящее под зна­ком суммы, на Dt и перейдя к пределу с учетом того получим одну из форм интеграла Дюамеля:

                           

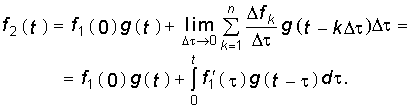
Уравнение (8.8) отражает реакцию цепи на заданное воздействие, поскольку аппроксимирующая функция стремится к ис­ходной.

Вторая форма интеграла Дюамеля может быть получена с по­мощью теоремы свертки (см. § 7.1):

                                         

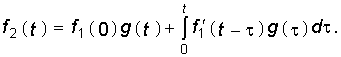
Наконец, интегрируя по частям выражения, стоящие в уравне­ниях (8.8) и (8.9), получаем третью и четвертую формы интеграла Дюамеля:

                                      

                                      

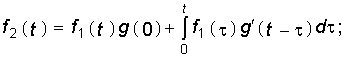
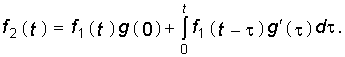
Применение той или иной формы интеграла Дюамеля диктуется удобством и простотой вычисления подынтегральных выражений.

Пример. Запишем реакцию цепи (см. рис. 8.1) на напряжение, изображенное на рис. 8.3 с помощью интеграла Дюамеля (8.8). Переходная характеристика дан­ной цепи имеет вид .

После нахождения переходной функции определяем число участков интегри­рования, где функция непрерывна и дифференцируема. Определяем значение  на этих участках. Для рассматриваемого воздействия таких участков будет три: , , . Необходимость включения третьего участка объясняется тем обстоятельством, что несмотря на прекращение входного воз­действия в силу переходных процессов (см. гл. 6) в цепи будет наблюдаться ос­таточная реакция. Для каждого из выделенных участков запишем уравнение (8.8) с учетом реакций предыдущих участков:

на участке

    

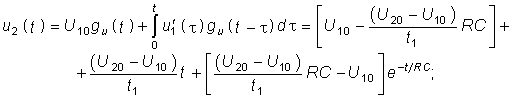
на участке

                   

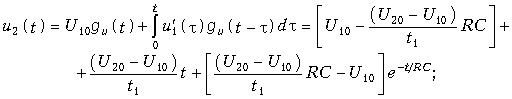
на участке

            

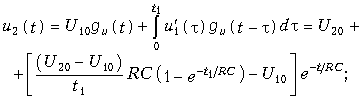
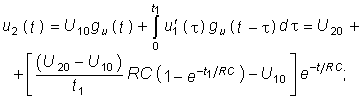
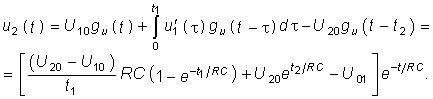
В случае, когда воздействие прикладывается к активной цепи (рис. 8.4, а), расчет переходных процессов можно вести методом наложения. При этом вначале расчет ведется с помощью интеграла Дюамеля для пассивной цепи (рис. 8.4, б), затем определяется клас­сическим или операторным методом реакция цепи при включении рассматриваемой ветви к активному двухполюснику (рис. 8.4, в). Результирующая реакция находится как сумма реакций: .