2 курс 1 часть / отц / экзамен / шпоры / билет 26

Метод узловы́х потенциалов — метод расчета электрических цепей путем записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях.

Очень часто необходимым этапом при решении самых разных задач электроники является расчет электрической цепи. Под этим термином понимается процесс получения полной информации о напряжениях во всех узлах и о токах во всех ветвях заданной электрической цепи. Для расчета линейной цепи достаточно записать необходимое число уравнений, которые базируются на правилах Кирхгофа и законе Ома, а затем решить полученную систему.

Однако на практике записать систему уравнений просто из вида схемы удается только для очень простых схем. Если в схеме более десятка элементов или она содержит участки типа мостов, то для записи системы уравнений уже требуются специальные методики. К таким методикам относятся метод узловых потенциалов и метод контурных токов.

Метод узловых потенциалов не привносит ничего нового к правилам Кирхгофа и закону Ома. Данный метод лишь формализует их использование настолько, чтобы их можно было применить к любой, сколь угодно сложной цепи. Иными словами, метод дает ответ на вопрос «как использовать законы для расчета данной цепи?».

Методика

1. Записывают уравнения для токов в ветвях схемы по обобщенному закону Ома.

2. Записывают для всех узлов, кроме одного, уравнения по 1 закону Кирхгофа.

3. В уравнения 1-ого закона Кирхгофа подставляют токи из уравнений обобщенного закона Ома, раскрывают скобки и проводят подобие относительно потенциалов узлов.

Переход к эквивалентной схеме

Метод узловых потенциалов применяется к эквивалентной схеме. Если изначально дана реальная схема, то для нее необходимо составить эквивалентную схему и дальнейший расчет производить с ней. Таким образом, схема, к которой применяется метод узловых потенциалов, не содержит никаких реальных элементов (транзисторов, диодов, ламп, гальванических элементов, пассивных элементов с паразитными параметрами и т.д.).

выбор обозначений

Составление системы уравнений

Перед началом расчёта выбирается один из узлов, потенциал которого считается равным нулю. Затем узлы нумеруются, после чего составляется система уравнений.

Слева от знака равенства записывается потенциал заданного узла, умноженный на сумму проводимостей ветвей, примыкающих к нему, минус потенциалы узлов, примыкающих к данному, умноженные на проводимости ветвей, соединяющих их с данным узлом.

Справа от знака равенства записывается сумма всех источников токов, примыкающих к данному узлу, если источник направлен в сторону рассматриваемого узла, то он записывается со знаком «+», если же он направлен от узла — то со знаком «−». Если это источник ЭДС, то он записывается как значение ЭДС, умноженное на проводимость ветвей, соединяющей их с данным узлом.

2 Классический метод анализа переходных процессов

Классический метод анализа переходных процессов основан на составлении системы дифференциальных и алгебраических уравнений с использованием уравнений для элементов и законов Кирхгофа для мгновенных токов и напряжений в цепи:

Для определения интересующей реакции систему исходных уравнений путем исключения остальных переменных приводят к одному линейному уравнению n-го порядка с постоянными коэффициентами:

,

(1.4)

где i(t) - искомая переменная; f(t) - правая часть, обусловленная возмущающими силами, т.е. функциями источников.

Напомним известные из курса математики сведения о решении линейных дифференциальных уравнений. Общее решение линейного дифференциального уравнения (1.4) определяется в виде суммы двух составляющих:

i(t) = i_св(t) + i_вын(t) .

(1.5)

Первая составляющая называется свободной или собственной и определяется как общее решение соответствующего однородного уравнения, которое получается из (1.4) путем приравнивания нулю правой части f(t) = 0:

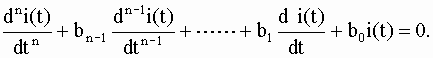
(1.6)

Для определения общего решения (1.6) составляется характеристическое уравнение, которое получается из (1.6) путем замены k -той производной на p^k . При этом сама искомая переменная заменяется на единицу. Характеристическое уравнение

pⁿ + b_n-1p^n-1 + ........... +b₁p + b₀ = 0

(1.7)

является алгебраическим уравнением степени n и его корни p_k определяют общее решение однородного дифференциального уравнения:

,

(1.8)

где A_k - постоянные интегрирования.

Решение (1.8) записано для случая различных корней p_k . Входящие в (1.8) n постоянных интегрирования определяются по известным независимым начальным условиям.

Заметим, что в однородном дифференциальном уравнении (1.6) правая часть приравнивается нулю, что означает отсутствие в цепи внешнего воздействия, т.е. источника. Поэтому токи и напряжения в ветвях цепи будут определяться только параметрами и свойствами самой цепи, а также начальным запасом энергии. Физически очевидно, что для реальных цепей собственная составляющая i_св(t) при отсутствии источников должна стремиться со временем к нулю. Эта составляющая существует во время переходного процесса.

Вторая составляющая i_вын(t) решения (1.5) называется вынужденной и представляет собой частное решение неоднородного дифференциального уравнения (1.4) (с ненулевой правой частью). Из математики известно, что вид частного решения определяется видом правой части уравнения. В частности, если правая часть f(t) - константа, то и частное решение ищется в виде константы. Если правая часть является гармонической функцией с определенными частотой, амплитудой и начальной фазой, то и частное решение будет гармонической функцией той же частоты, для которой нужно определить амплитуду и начальную фазу.

Таким образом, вынужденная составляющая обусловлена воздействием источников в цепи и при t искомая переменная i(t)  i_вын(t). Поэтому вынужденная составляющая называется установившейся и определяется как установившееся значение (в случае постоянной вынуждающей силы) или как установившаяся функция (в случае гармонической вынуждающей силы) для искомой переменной в цепи после коммутации

i_вын(t) = i_уст(t)

(1.9)

Необходимо отметить, что определение вынужденной составляющей в случае воздействия сигналов более сложной формы, чем упомянутые выше, представляет достаточно сложную задачу.

В заключении приведем рекомендуемый порядок расчета переходных процессов классическим методом.

1. Определить независимые начальные условия i_Lk(0₊) и u_Ck(0₊) с использованием законов коммутации.

2. Для цепи после коммутации составить систему уравнений Кирхгофа с использованием уравнений для элементов.

3. Полученную систему разрешить относительно искомой переменной. При этом получится одно дифференциальное уравнение n-ой степени, где n равно общему числу индуктивностей и емкостей, в которых можно задавать независимые начальные условия.

4. Определить решение полученного дифференциального уравнения

 

(1.10)

где i_вын(t)=i_уст(t) -вынужденная (установившаяся) составляющая; p_k - корни характеристического уравнения; A_k - постоянные интегрирования, определяемые из начальных условий.

Далее классический метод будет использован для анализа переходных процессов в простейших RL, RC и RLC- цепях.