116

Содержание

Тема 1. Основные понятия теории вероятностей…………………………….3

Тема 2. Классические теоремы теории вероятностей………………………12

Тема 3. Повторные независимые испытания………………………………..20

Тема 4. Случайные величины и законы их распределения………………...32

Тема 5. Числовые характеристики случайных величин……………………39

Тема 6. Основные дискретные случайные величины и их числовые характеристики…………………………….………………………. 48

Тема 7. Основные непрерывные случайные величины и их числовые характеристики……………….……………………………………. 55

Тема 8. Закон больших чисел и центральная предельная теорема………..64

Тема 9. Основные понятия математической статистики. Числовые характеристики…………………………….………………………..70

Тема 10. Статистические оценки…………………………………………….85

Тема 11. Корреляция и регрессия……………………………………………94

Тема 12. Проверка статистических гипотез………………………………..109

Литература…………………………………………………………………...117

Приложения………………………………………………………………….

Михаил Филиппович Тиунчик

РУКОВОДСТВО К РЕШЕНИЮ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

Учебное пособие

Н/К

Редактор Г.С.Одинцова

ЛР № 020756 от 02.04.98г.

Подписано в печать . Формат 6084/16. Бумага писчая.

Печать офсетная. Усл.п.л. 7,0. Уч.-изд.л. 5,0. Тираж 830 экз.

Заказ № .

680042, г.Хабаровск, ул.Тихоокеанская, 134, ХГАЭиП, РИЦ.

ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Испытания и события. Невозможное, достоверное и случайное события. Виды случайных событий. Классическое определение вероятности. Относительная частота и ее устойчивость. Ограниченность классического определения вероятности. Статистическое определение вероятности. Геометрические вероятности. Элементарные события. Пространство элементарных событий. Противоположное событие, сумма и произведение событий. Алгебра событий. Аксиоматическое определение вероятности. Вероятностное пространство. Принципы практической невозможности и практической достоверности событий. Предмет теории вероятностей. Перестановки, сочетания, размещения и формулы для вычисления их числа. Применение комбинаторики к подсчету вероятностей.

Л и т е р а т у р а

[2], гл. 1, § 1,2, гл.2, § 1,2; [3], гл.1, гл. 2, 2.1-2.3, 2.5, гл.3, 3.1; [5], гл.1, § 1-6, гл.2, § 4; [6], гл.1; [7], гл.1; [8], гл.1, § 1-3, § 7; [9], гл.1, § 1-4; [10], гл.1, § 1-3; [11], гл.26, § 182-185; [12], ч.2, гл.1, § 1,2; [13], гл.20, § 1,2; [15], гл.1, § 1-3, гл.2, § 1-3; [16], гл.1, 1.1-1.3, 1.7.

О с н о в н ы е ф о р м у л ы и м е т о д и ч е с к и е

у к а з а н и я

Вероятность Р(А) события А вычисляется как отношение числа m благоприятных этому событию исходов к общему числу n равновозможных, единственно возможных и несовместных исходов:

Р(А) = . (1.1)

Пусть всем возможным результатам испытания соответствуют точки множества , а данному событию А – точки множества S, которое является частью множества  (S). Тогда

Р(А) = , (1.2)

где mes G - длина, площадь, объем множества G.

Частота W(А) события А находится на основании результатов опыта по формуле

W(А) = , (1.3)

где n – общее число фактически проведенных испытаний, а m – число появления события А.

Число перестановок Р_n из n элементов находится по формуле

Р_n = n! . (1.4)

По определению принимают равенство 0!=1.

Число сочетаний изn элементов по m элементов вычисляется по формуле

(1.5)

В частности, . Это согласуется с тем, что в множестве изn элементов имеется только одно подмножество из 0 элементов – пустое множество.

Число размещений изn элементов по m находится по формуле

. (1.6)

При решении задач на классическое определение вероятности прежде всего выясняют, в чем состоят исходы испытания и какие исходы благоприятны данному событию. Затем непосредственно вычисляют вероятность события по формуле (1.1), предварительно вычислив общее число исходов n и число m благоприятных исходов. При этом надо убедиться, что указаны все элементарные исходы и что они равновозможны и несовместны.

При выявлении элементарных исходов иногда допускаются ошибки. Поясним это на примере. Монета бросается 2 раза. Найти вероятность того, что герб выпадет оба раза (событие А).

Решая эту задачу, рассуждают так. Герб может выпасть 2 раза, 1 раз и 0 раз (ни разу). Считают, что элементарных исходов три: {0,1,2}. Эти исходы несовместны и единственно возможны. Благоприятен А один исход (герб выпал оба раза). Тогда Р(А) = .

Приведенное решение содержит ошибку. На самом деле описанные выше исходы не являются равновозможными, и поэтому нельзя применять классическое определение вероятности. Пространством элементарных событий является следующее множество равновозможных событий: {ГГ, ГЦ, ЦГ, ЦЦ}. Через Г обозначено появление герба, а через Ц – цифр (решки). Ошибка первоначального рассуждения в том, что учтен только один из симметричных исходов ГЦ, ЦГ. Таким образом, Р (А) = .

Решение многих задач основывается на двух фундаментальных правилах, называемых правилами суммы и произведения.

Правило суммы можно сформулировать так: если некоторый объект можно выбратьn₁ способами, а объект -n₂ способами, причем любой способ выбора отличается от любого способа выбора, то выбор «или» можно сделатьn₁ + n₂ способами.

Правило суммы обобщается на любое конечное число объектов.

Правило произведения состоит в следующем: если объект можно выбратьn₁ способами, и после каждого такого выбора объект можно выбратьn₂ способами, то выбор пары (,) может быть осуществленn₁n₂ способами.

Это правило обобщается на случай k объектов. Тогда число комбинаций () есть N=n₁…n_k .

В частности, может быть k одинаковых групп по n элементов в каждой. Пусть на r-м шаге выбирается элемент из r-й группы. Тогда число N различных комбинаций есть n^k .

Приведем пример. Цифровой замок содержит на общей оси 4 диска, каждый из которых разделен на 6 секторов, отмеченных цифрами. При наборе кода каждый диск может быть установлен в любую из 6 позиций. Следовательно, замок содержит N=6⁴ различных четырехзначных кодов.

При решении задач встречаются выборки без возвращения и выборки с возвращением. Выборку без возвращения наглядно можно представить как последовательный набор из совокупности n перенумерованных шаров, находящихся в урне. Вынутые шары в урну не возвращаются. При выборке с возвращением шары вынимаются, запоминаются и возвращаются в урну. В последнем случае один и тот же шар может быть выбран более одного раза. Если производится выбор с возвращением, то число различных выборок объема k из множества в n элементов равно n^k.

К выборкам без возвращения относятся размещения, перестановки и сочетания, которые часто применяются при непосредственном вычислении вероятностей по формуле (1.1). Для вычисления числа перестановок, сочетаний и размещений применяются, соответственно, формулы (1.4)-(1.6).

Перестановки из n элементов можно понимать как размещения из n элементов по n элементов.

Важно уяснить различие между сочетаниями и размещениями. Поясним это на примере.

В группе 25 студентов. Сколькими способами можно выбрать: 1) трех делегатов на конференцию; 2) актив группы (старосту, заместителя старосты, профорга)? В первой ситуации нас интересует только состав, поэтому речь идет о сочетаниях. Применяя формулу (1.5), получим N==2300. Во второй ситуации в каждой выбранной тройке студентов можно перераспределять должности, т.е. речь идет о составе и порядке (о размещениях). Тогда по формуле (1.6)N=Р₃=23003!=13800.

При подсчете числа сочетаний для уменьшения вычислительной работы надо руководствоваться следующим. Если m, то применяют формулу

,

которая следует из (1.5). Если m>, то надо воспользоваться свойством и к вычислению применять последнюю формулу.

Например, . Вычислим теперь. Воспользовавшись указанным свойством, получим.

Р е ш е н и е т и п о в ы х з а д а ч

Задача 1. Подарочный набор состоит из яблока, апельсина и шоколада. Сколько различных видов подарочных наборов можно составить, если имеется четыре сорта яблок, три сорта апельсинов и семь сортов шоколада?

Решение. Яблоко для подарочного набора можно выбрать 4 способами, апельсин – 3 способами, шоколад – 7 способами. Применяя правило произведения, находим, что из имеющегося ассортимента продуктов можно образовать N== 84 разных подарочных наборов.

Задача 2. Телефонный номер состоит из шести цифр. Сколько абонентов можно подключить к АТС, если предположить, что все цифры номера различны?

Решение. Из множества цифр, содержащего 10 различных элементов, выбираются 6 элементов. Надо учитывать порядок расположения выбранных элементов. Следовательно, необходимо найти число размещений без повторений из десяти элементов по 6 элементов в каждом, т.е. А. Значит, согласно (1.6) к АТС можно будет подключить Аабонентов.

Задача 3 . На окружности даны 6 точек. Сколько треугольников можно вписать в окружность так, чтобы их вершинами были указанные точки?

Решение. Из множества, содержащего 6 различных элементов, выбираются 3 элемента, так как вписанный треугольник однозначно определяется тремя точками, лежащими на окружности. Порядок элементов роли не играет. Следовательно, необходимо найти число сочетаний из шести элементов по три по формуле (1.5). Значит, можно вписать Сразличных треугольников.

Задача 4. Для некоторого района планом предусмотрено строительство школы, детского сада и молодежного кафе. Скольким числом способов указанные объекты можно пустить в строй?

Решение. Все три объекта в плановый период должны быть построены. Однако порядок введения их в строй может быть разным. Следовательно, число способов N равно числу перестановок из трех элементов. Тогда, согласно формуле (1.4) N=P₃= 3! = 6, т.е. школа, детский сад и молодежное кафе могут быть пущены шестью различными способами.

Задача 5. Какова вероятность того, что наудачу выбранное целое число от 1 до 30 включительно является делителем числа 40?

Решение. Испытание состоит в том, что выбирается наудачу целое число. Число n возможных исходов испытания равно 30. Событие А означает, что наудачу взятое число является делителем числа 40. Этому событию благоприятствует 7 исходов испытания: {1; 2; 4; 5; 8; 10; 20}. Следовательно, по формуле (1.1) получим, что Р(А)=.

Задача 6. Группа туристов из 12 юношей и 8 девушек выбирает по жребию хозяйственную команду в составе трех человек. Какова вероятность того, что в составе этой команды окажется двое юношей и девушка?

Решение. Испытание состоит в том, что из 20 человек выбирают три человека. Так как выбор осуществляется по жребию, то все исходы испытания равновозможны и, кроме того, они несовместны. Число исходов испытания n=С, так как выборка состоит из трех элементов и порядок их расположения в выборке не учитывается. Пусть событие А состоит в том, что в составе выбранных окажутся двое юношей и девушка. Двух юношей из 12 можно выбрать Сспособами и после каждого такого выбора одну девушку из 8 можно выбрать Сспособами. По правилу произведения, событию А благоприятствуютm=исходов испытания. Искомая вероятность вычисляется по формуле (1.1):Р(А)=.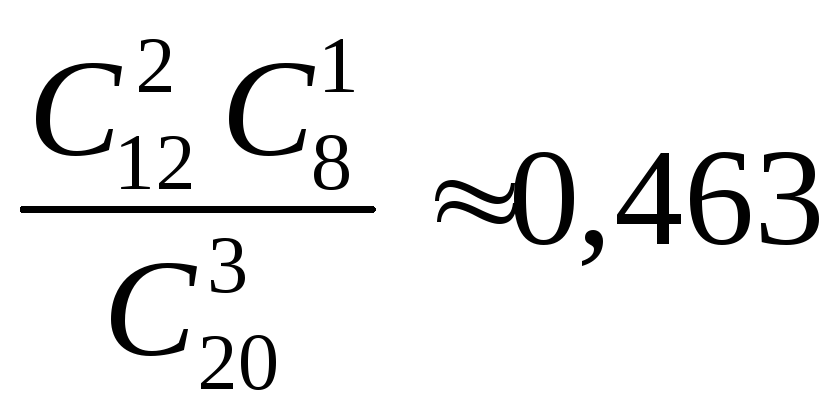

Примечание: Эта задача связана с гипергеометрическим распределением, которое часто встречается. При решении подобных задач для контроля правильности решения рекомендуется сделать проверку по правилу: сумма нижних (верхних) индексов в произведении сомножителей числителя равна нижнему (верхнему) индексу знаменателя. В нашем примере это выполняется (12+8=20, 2+1=3), что говорит о правильности решения.

Задача 7. На книжной полке случайным образом расставлены 4 книги по высшей математике и 3 книги по теории вероятностей и математической статистике. Определить вероятность того, что книги по одному и тому же предмету окажутся рядом.

Решение. Испытание состоит в том, что 7 книг ставятся на полку. Так как они ставятся на полку произвольно, то все исходы испытания равновозможны и, кроме того, они несовместны. Для вычисления общего числа исходов испытания применим формулу (1.4). Число перестановок из 7 элементов: n=Р₇=7!. Событию А, состоящему в том, что книги по одному и тому же предмету окажутся рядом, благоприятствуют m=исходов испытания. Действительно, комплект книг по высшей математике может быть упорядочен 4! способами, а по теории вероятностей и математической статистике – 3! способами. Кроме того, сами комплекты книг могут быть упорядочены двумя способами. Таким образом, искомая вероятностьР(А) =

Задача 8. В урне находятся девять карточек, на каждой из которых написана одна из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9. Извлечены и разложены наугад в ряд три карточки. Какова вероятность того, что получившееся трехзначное число состоит только из нечетных цифр?

Решение. Испытание состоит в том, что из множества, содержащего 9 различных элементов, выбираются три элемента. Порядок существенен. Элементы не могут повторяться, т.е. речь идет о размещениях без повторений. Следовательно, число исходов испытания n=. Пусть событие А состоит в том, что получившееся трехзначное число состоит только из нечетных цифр. Числоm таких трехзначных чисел будет равно числу размещений из 5 по 3 (m=). Тогда по формуле (1.1)Р(А)=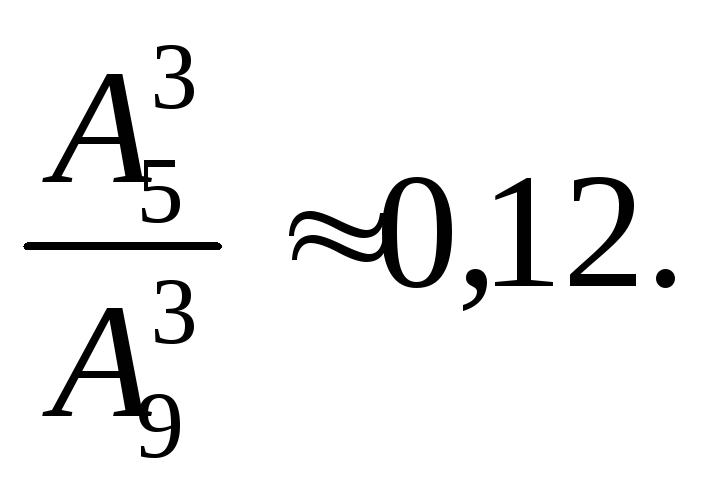

Задача 9. Территория нефтебазы имеет форму прямоугольника со сторонами а=40 м, b=50 м. На территории имеется 4 круглых нефтебака диаметром 10 м каждый. Какова вероятность поражения нефтебаков снарядом, попавшим на территорию нефтебазы, если попадание снаряда в любую точку равновозможно?

Решение. В формуле (1.2) mes - площадь территории нефтебазы. Она равна 4050=2 000 (м²). Mes S равна суммарной площади верхних поверхностей всех четырех нефтебаков. Каждая такая поверхность представляет собой круг радиуса 5 м. Следовательно, mes S=4(м²). Тогда по (1.2) искомая вероятность Р(А)=

Задача 10. Из 980 абитуриентов, подавших заявление на первый курс института, были зачислены 460 человек. Определить относительную частоту поступления в институт.

Решение. Относительная частота поступления в институт (событие А) вычисляется по формуле (1.3): W(А)=.

З а д а ч и

1. В районе 8 населенных пунктов. Сколько различных маршрутов для самолета можно составить, если известно, что каждый маршрут соединяет три пункта?

2. Сколько различных «слов», состоящих не менее чем из четырех разных букв, можно образовать из букв слова «ученик»?

3. На четырех карточках написаны числа 1, 3, 4, 5. Найти вероятность того, что сумма чисел на трех произвольно выбранных карточках делится на 4.

4. Данное предприятие в среднем выпускает 20% продукции высшего сорта и 70% продукции первого сорта. Найти вероятность того, что случайно взятое изделие окажется первого или высшего сорта.

5. В цехе работают 7 мужчин и 5 женщин. По табельным номерам наудачу отобраны 3 человека. Определить вероятность того, что все отобранные 1) мужчины, 2) женщины.

6. В группе трое юношей и 21 девушка. По жребию разыгрываются два билета в театр. Какова вероятность того, что в театр пойдут: 1) две девушки, 2) одна девушка и один юноша, 3) лица одного пола?

7. Из 6 менеджеров, 4 бухгалтеров и 5 инженеров необходимо случайным образом сформировать комиссию в составе 6 человек для анализа работы фирмы. Найти вероятность того, что в комиссию войдут 3 менеджера, 2 бухгалтера и один инженер.

8. На склад торгового центра завезено 120 мешков сахарного песка. Среди этих мешков 10 имели избыточную влажность. Для продажи случайно отобрали 15 мешков. Определить вероятность того, что на продажу поступило 2 мешка сахара с избыточной влажностью.

9. Из пяти букв разрезной азбуки составлено слово «книга». Ребенок, не имеющий читать, рассыпал эти буквы, а затем собрал в произвольном порядке. Найти вероятность того, что у него снова получилось слово «книга».

10. Определить вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы а, а, а, н, н, с, получится слово «ананас».

11. Наудачу взятый телефонный номер состоит из 6 цифр. Какова вероятность того, что в нем все цифры различны?

12. В прямоугольнике с основанием 8 см и высотой 6 см вписан эллипс. Указать вероятность того, что точка, брошенная наудачу в прямоугольник, окажется внутри эллипса.