1. Системы координат на плоскости.

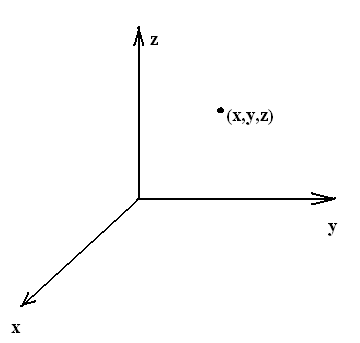
2. Системы координат в пространстве.

Декартова прямоугольная система координат

Сферическая система координат.

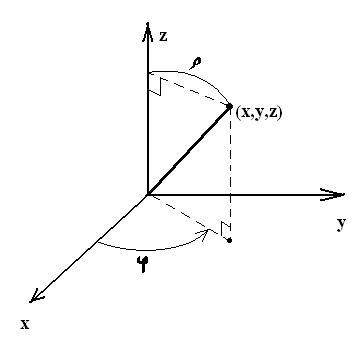
Цилиндрическая система координат (трубы, туннели…).

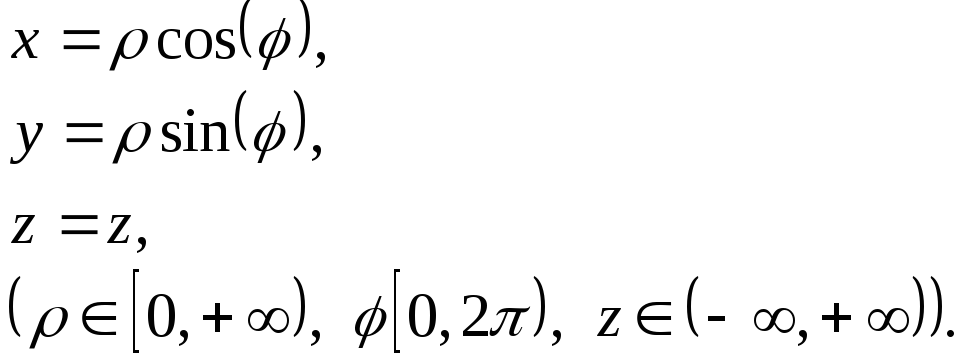
3. Способы задания кривых на плоскости.

4. Способы задания кривых и поверхностей в пространстве.

Существует три основных способа задания кривых и поверхностей в пространстве:

• Явное.

• Неявное.

• Параметрическое.

Способы задания поверхностей

- Явное:

Пример: График функции двух переменных (гиперболический параболоид).

Еще одним способом наглядного представления функции двух переменных, широко используемым на практике, является ее представление в виде изолинии – ГМТ на плоскости, для которых функция принимает постоянные значения: . Таким образом, каждая изолиния задается неявно с помощью уравнения.

- Неявное:

Пример: (однополостный гиперболоид),(плотность, как характеристика, распределенная в пространстве).

- Параметрическое:

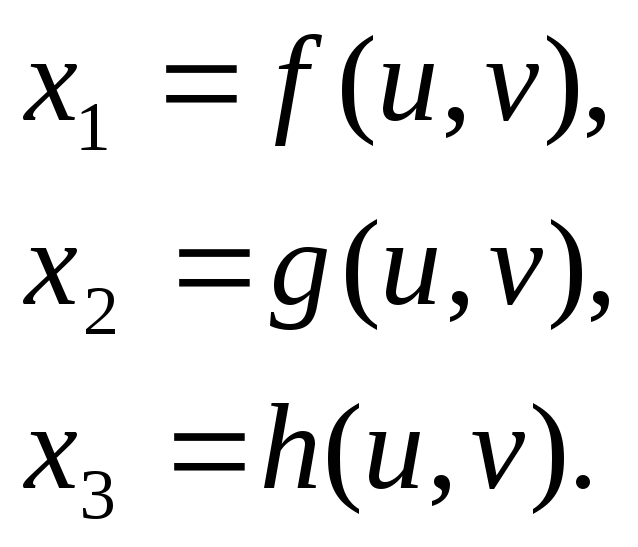
Пример: боковая поверхность кругового цилиндра радиуса R и высотой H в цилиндрической СК:

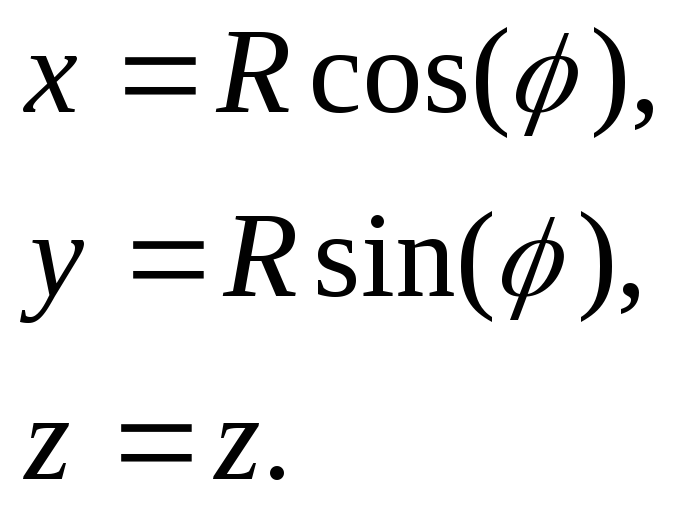
Способы задания кривых

- Неявное:

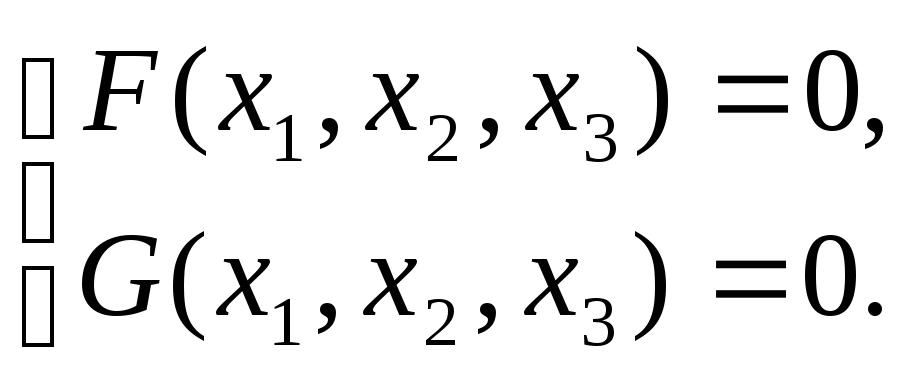
Данная система имеет следующую геометрическую интерпретацию: ее решение соответствует линии пересечения двух неявно заданных поверхностей (если она существует).

- Параметрическое:

Если принять следующее параметрическое задание поверхности:

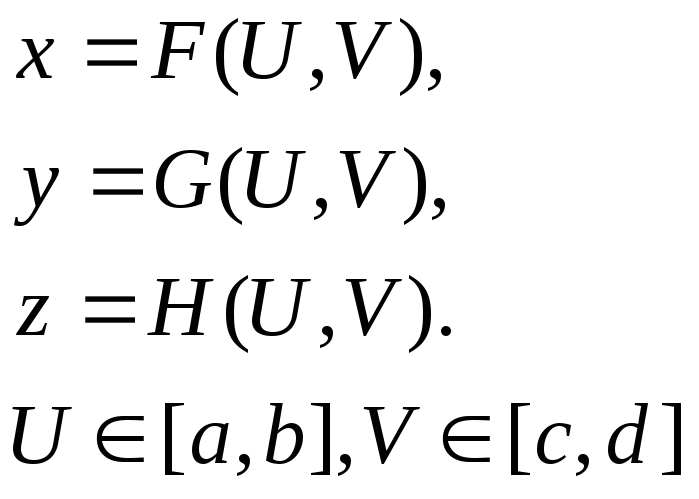
То с помощью замены можно всегда перейти к параметрическому заданию исходной поверхности:

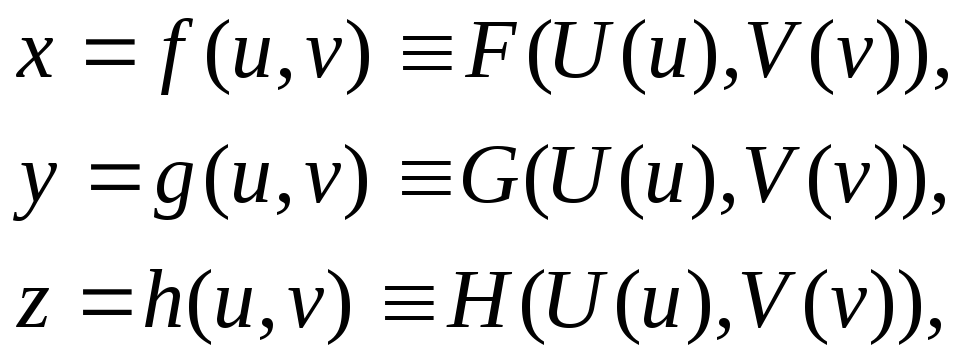
при котором область допустимых значений параметров u и v представляет собой единый квадрат . В этом случае параметрыu и v будем называть нормализованными.

Величины U, V называют внутренними криволинейными координатами на поверхности. Также как и на плоскости, они могут использоваться для явного, неявного или параметрического задания кривой на поверхности.

Пример: если , то при подстановке в вышеуказанные уравнения получим координатную линию на поверхности (параметрически заданная пространственная кривая). Аналогично для уравненияи т.д.

5. Преобразования симметрии относительно заданной точки.

делаем перенос мировой системы координат:

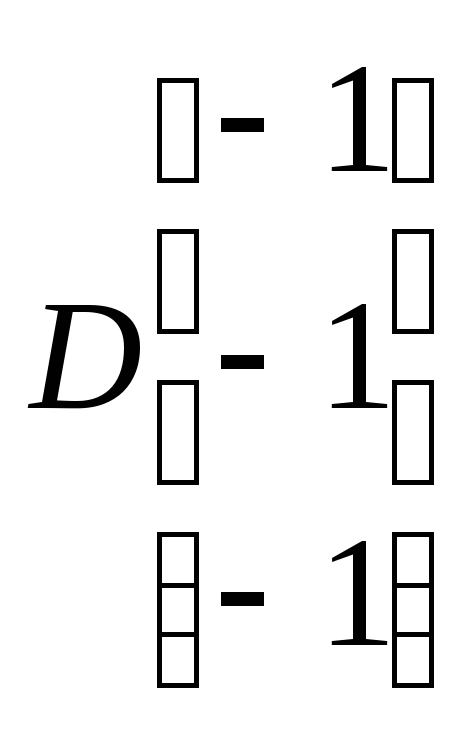T(V)

*T(V)

Переносим систему координат обратно:

T(V)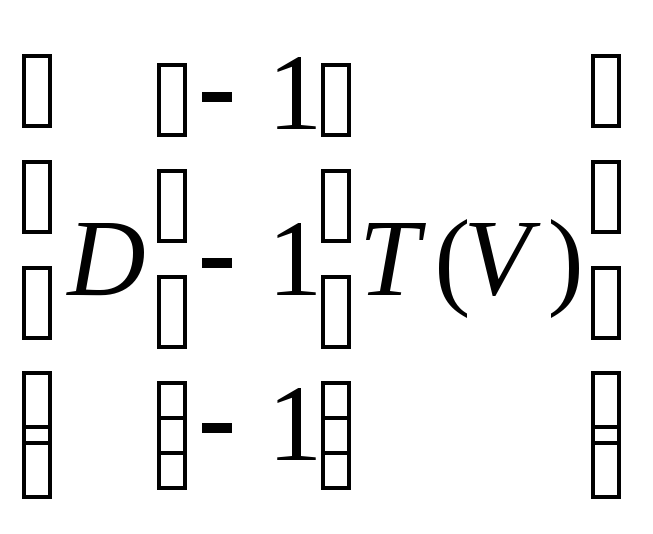

6. Преобразования симметрии относительно заданной прямой.

Симметрия – это то же самое отражение, поэтому задача преобразования симметрии относительно заданной прямой сводится к задаче отражения относительно произвольной прямой.

Отражение в двумерном пространстве

Задача отражения относительно произвольной прямой сводится к задаче отражения относительно прямой проходящей через начало координат посредством следующих действий:

1. Перемещение линии и объекта таким образом, чтобы линия прошла через начало координат.

2. Поворот линии и объекта вокруг точки начала координат до совпадения с одной из координатных осей.

3. Отражение относительно координатной оси.

4. Обратный поворот вокруг начала координат.

5. Перемещение в исходное положение.

В матричном виде данное преобразование имеет представление:

,

где - матрица перемещения,R – матрица поворота вокруг начала координат, - матрица отражения.

В общем случае матрица отражения имеет следующий вид:

- отражение относительно прямой y=0.

- отражение относительно прямой x=0.

- отражение относительно прямой y=x.

У каждой из этих матриц определитель равен -1. В общем случае, если определитель матрицы преобразования равен -1, то преобразование дает полное отражение.

7. Преобразования симметрии относительно заданной плоскости.

Некоторые ориентации трехмерного объекта нельзя получить одними вращениями, требуются преобразования отражения. В трехмерном пространстве отражение происходит относительно плоскости. По аналогии с двумерным отражением, трехмерное отражение относительно плоскости эквивалентно вращению вокруг оси в трехмерном пространстве в четырехмерное и обратно в исходное трехмерное пространство. Для чистого отражения детерминант матрицы равен -1.

В общем случае матрица отражения имеет следующий вид:

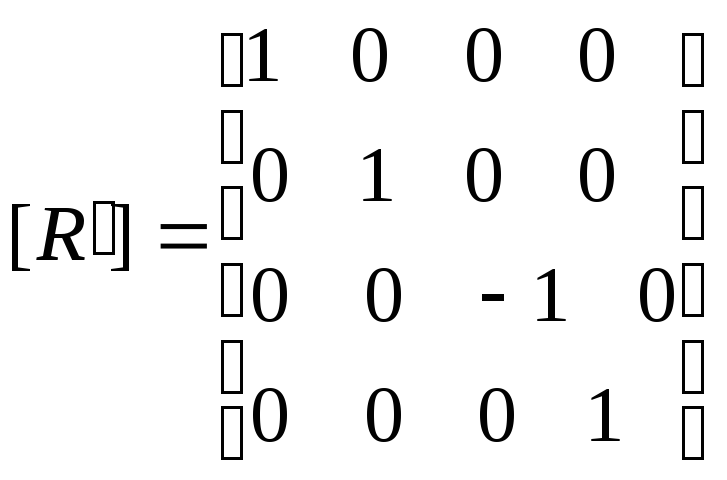- отражение относительно плоскости xy.

- отражение относительно плоскости yz.

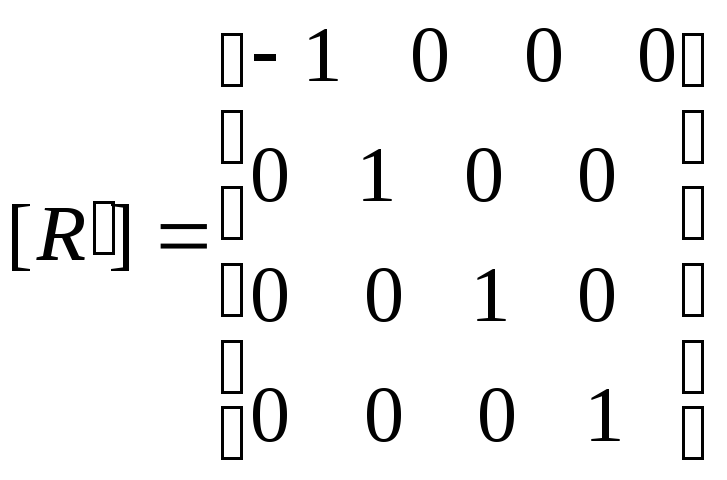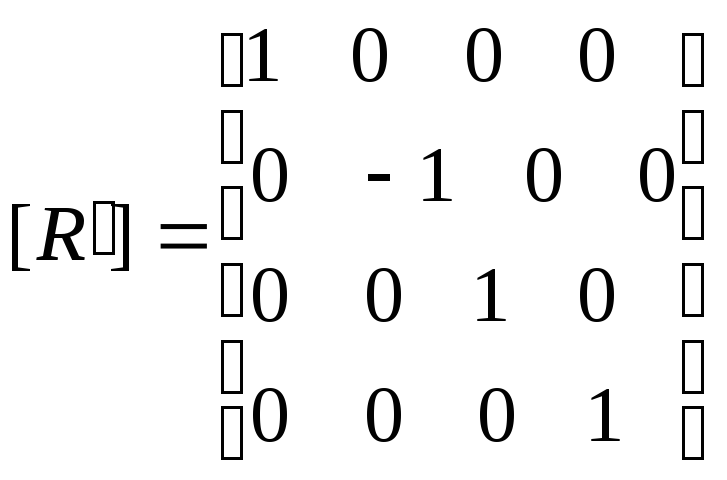- отражение относительно плоскости xz.

Симметрии относительно плоскостей , осейи точки(начала координат) задаются матрицами

Симметрии относительно произвольных плоскостей и прямых можно получить по той же формуле, что и растяжения, взяв в качестве нужную комбинацию чисели. Однако если мы хотим, чтобы полученное преобразование было действительно симметрией нужного вида, векторы, для которых, должны быть перпендикулярны, то есть, их скалярное произведение должно быть равно:. При отыскании нужных векторов полезно иметь в виду, что вектор с координатамиперпендикулярен плоскости. В частности, матрица симметрии относительно плоскостиимеет вид