
Лекция 6 Базовая графика
Вывод изображения на экран дисплея и разнообразные действия с ним, в том числе и визуальный анализ, требуют от пользователя известной геометрической грамотности. Геометрические понятия, формулы и факты, относящиеся прежде всего к плоскому и трехмерному случаям, играют в задачах компьютерной графики особую роль.
Геометрические фигуры представлены в памяти ЭВМ числовыми моделями, содержащими параметры формы и параметры положения фигуры, а также геометрические условия формирования фигуры. В начертательной геометрии рассматриваются способы описания фигур с помощью параметров. Минимальное количество параметров, необходимых для описания фигуры, называется ее параметрическим числом. Точка задается двумя параметрами на плоскости и тремя в пространстве. Прямая задается двумя параметрами на плоскости и четырьмя в пространстве.
Плоскость тремя параметрами. Точки, прямые и плоскости описываются параметрами положения. Отрезок прямой на плоскости задается четырьмя и в пространстве шестью параметрами, из которых один (длина отрезка) является параметром формы. Окружность задается тремя параметрами, из которых один (радиус окружности) является параметром формы. Числовые модели фигур могут быть заданы аналитически в виде неявного уравнения либо параметрически в виде параметрического уравнения. Например, в случае окружности параметрами положения являются координаты хс ус ее центра, параметром формы величина R радиус. С помощью этих параметров может быть написано неявное уравнение окружности:
![]()
Та же окружность может быть задана параметрическим уравнением, где добавлен еще один переменный параметр центральный угол а, определяющий положение точки на окружности:
![]()
С помощью последних уравнений можно воспроизвести процесс построения отдельных точек окружности, определяя ее как множество точек. В начертательной геометрии есть понятие определителя фигуры, который состоит из частей: постоянной (в случае окружности это, например, xc, yc, R ) и переменной ( ). Первая геометрическая, вторая алгоритмическая части определителя. Легко видеть, что алгоритмическая часть определителя задает алгоритм воспроизводства всего множества точек, принадлежащих фигуре, которая имеет данную геометрическую часть определителя. Все эти понятия являются фундаментальными для компьютерной графики.
Аффинные преобразования на плоскости
Аффинное преобразование это такое преобразование, которое сохраняет параллельность линий, но не обязательно углы или длины. В компьютерной графике все, что относится к двумерному случаю, принято обозначать символом 2D (2-dimension). Допустим, на плоскости введена прямолинейная координатная система. Тогда каждой точке М ставится в соответствие упорядоченная пара чисел (х, у) ее координат (рис. 1).
В
Где -
-
произвольные числа

Указанные выше формулы можно рассматривать двояко: либо сохраняется точка и изменяется координатная система в этом случае произвольная точка М остается той же, изменяются лишь ее координаты (х, у) (х*, у*) , либо изменяется точка и сохраняется координатная система в этом случае формулы задают отображение, переводящее произвольную точку М(х, у) в точку М*(х*, у*), координаты которой определены в той же координатной системе. В дальнейшем будем интерпретировать формулы, как правило, что в заданной системе прямолинейных координат преобразуются точки плоскости. В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих хорошо прослеживаемые геометрические характеристики. При исследовании геометрического смысла числовых коэффициентов в формулах для этих случаев удобно считать, что заданная система координат является прямоугольной декартовой. Наиболее часто применяются следующие приемы компьютерной графики: перенос, масштабирование, поворот, отражение. Алгебраические выражения и рисунки, поясняющие данные преобразования сведем в табл.1.
Аффинные преобразования на плоскости

Под переносом понимается смещение примитивов вывода на один и тот же вектор. Масштабирование это увеличение или уменьшение всего изображения либо его части. При масштабировании координаты точек изображения умножаются на некоторое число. Под поворотом понимается вращение примитивов вывода вокруг заданной оси. ( В плоскости чертежа вращение происходит вокруг точки.) Под отражением понимают получение зеркального отображения изображения относительно одной из осей (например X). Выбор этих четырех частных случаев определяется двумя обстоятельствами: 1. Каждое из приведенных выше преобразований имеет простой и наглядный геометрический смысл (геометрическим смыслом наделены и постоянные числа, входящие в приведенные формулы). 2. Как доказывается в курсе аналитической геометрии, любое преобразование вида (*) всегда можно представить как последовательное исполнение (суперпозицию) простейших преобразований вида А, Б, В и Г (или части этих преобразований). Таким образом, справедливо следующее важное свойство аффинных преобразований плоскости: любое отображение вида (*) можно описать при помощи отображений, задаваемых формулами А, Б, В и Г. Для эффективного использования этих известных формул в задачах компьютерной графики более удобной является их матричная запись. Для объединения этих преобразований вводят однородные координаты. Однородными координатами точки называется любая тройка одновременно не равных нулю чисел x1 , x2 , x3 , связанных с заданными числами x и y следующими соотношениями:
![]()
Тогда точка M(х, у) записывается как M(hX, hY, h), где h 0 является масштабным множителем. Двумерные декартовы координаты могут быть найдены как
![]()
В проективной геометрии эти координаты вводятся для устранения неопределенностей, возникающих при задании бесконечноудаленных (несобственных) элементов. Однородные координаты можно интерпретировать как вложение промасштабированной с коэффициентом h плоскости в плоскость Z= h в трехмерном пространстве. Точки в однородных координатах записываются трехэлементными вектор-строками. Матрицы преобразования должны иметь размер 3х3. При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости. В самом деле, считая h = 1, сравним две записи: помеченную символом (*) и нижеследующую, матричную:
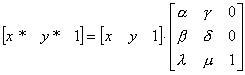
Теперь можно использовать композиции преобразований, применяя одно результирующее вместо ряда преобразований, следующих друг за другом. Можно, например, сложную задачу разбить на ряд простых. Поворот точки А около произвольной точки В можно разбить на три задачи: перенос, при котором В= 0 (где 0-начало координат); поворот; обратный перенос, при котором точка В возвращается на место и т. д. Композиция наиболее общего вида из операций Т, D, R, M имеет матрицу:
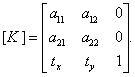
Верхняя часть размером 2х2 - объединенная матрица поворота и масштабирования, a tx и ty описывают суммарный перенос. К изложенным фундаментальным преобразованиям сводятся следующие: прокручивание перемещение окна на поверхности визуализации (если перемещение ограничено только направлениями вверх и вниз, то оно называется вертикальным прокручиванием);
трансфокация постепенное изменение масштаба изображения; кувыркание динамическое изображение примитивов вывода, вращающихся вокруг некоторой оси, ориентация которой непрерывно изменяется в пространстве; панорамирование постепенный перенос изображения с целью создания зрительного ощущения движения.
![]()
