
Лекция 1. Целые числа План
-
Отрицательные целые числа.
-
Операции над целыми числами. Свойства операций.
-
Свойства множества целых чисел.
Содержание
1.
В математике имеется ряд задач, не
разрешимых во множестве целых
неотрицательных чисел. Так, например,
никакое целое неотрицательное число х
не может
быть решением уравнения b
+ х = а
(а,
b
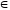 N0),
если а
< b.
Другими словами, уравнение 6 + х
= а
при а
< b
не имеет
решений во множестве N0.
N0),
если а
< b.
Другими словами, уравнение 6 + х
= а
при а
< b
не имеет
решений во множестве N0.
Вторая проблема,
не разрешимая во множестве целых
неотрицательных чисел, возникает при
описании процесса измерения величин.
Если величина х
имела значение
а
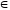 N0
и в результате
некоторого процесса уменьшилась на b
единиц, то
новое ее значение у
= а
– b
оказывается
неопределенным
в N0,
если а <
b.
N0
и в результате
некоторого процесса уменьшилась на b
единиц, то
новое ее значение у
= а
– b
оказывается
неопределенным
в N0,
если а <
b.
Неразрешимость этих задач приводит к необходимости расширить множество целых неотрицательных чисел. Это расширение достигается путем введения отрицательных целых чисел, которые в объединении с множеством N0 образуют множество целых чисел.
Отрицательные числа были известны математикам Китая около двух тысяч лет назад. Индийские математики Брахмагупта и Бхаскара II пользовались ими приблизительно в 650 г. В Европе отрицательные числа стали использоваться лишь в XVII веке.
Древнегреческий математик Диофант (III в.н.э.) свободно оперировал отрицательными числами. Они постоянно встречались в промежуточных вычислениях его «Арифметики». Однако и в XVI, и в XVII веках многие европейские математики не признавали отрицательных чисел, и если такие числа встречались при вычислениях, они называли их ложными, невозможными.
Положение изменилось после того, как в 1622 году Жирар (Франция) дал общеизвестный ныне способ геометрического изображения отрицательных чисел. Лет двадцать спустя отрицательные числа получили всеобщее распространение.
Возвращаясь к рассмотренным выше задачам, следует отметить, что их неразрешимость во множестве N0 связана с невозможностью найти разность a – b, если а < b.
Наша дальнейшая цель – построить такое числовое множество Z, которое включало бы в себя N0 и в котором операции сложения, вычитания и умножения были бы определены для всех элементов из Z и обладали бы всеми основными свойствами, которыми эти операции обладали в N0.
Для этого исследуем свойства всевозможных разностей вида a – b, где а и b являются натуральными числами и а > b.
Прежде
всего, каждая такая разность a
– b
единственным образом задает пару
натуральных чисел (а,
b)
и наоборот. Паре (а,
b),
где а >
b,
отвечает
единственное натуральное число
х
= a
– b.
В то же
время каждому числу х
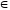 N соответствует
бесконечно много пар вида (с
+ х,
с),
так
как (с
+ х)
– с
= х
при
любом с
N соответствует
бесконечно много пар вида (с
+ х,
с),
так
как (с
+ х)
– с
= х
при
любом с
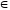 N.
N.
Если
одно и то же число х
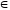 N
задается
двумя различными парами (а,
b)
и (с,
d),
то х
=
a
– b
и
х
= с –
d,
откуда
a
– b
=
с
–
d,
или
N
задается
двумя различными парами (а,
b)
и (с,
d),
то х
=
a
– b
и
х
= с –
d,
откуда
a
– b
=
с
–
d,
или
а + d = b + с. (1)
Таким образом, две пары (а, b) и (с, d) представляют одно и то же число тогда и только тогда, когда компоненты этих пар удовлетворяют соотношению (1). Далее найдем условия, которым удовлетворяют компоненты пар (а, b) и (с, d) при сложении чисел х = a – b и у = с – d. Очевидно, что х+у = (а – b) + (с – d) = (а + с) – (b + d). Следовательно, если числа х и у определяются парами (а, b) и (с, d), то их сумма должна определяться парой
(а + с, b + d). (2)
Теперь
для чисел х,
у
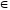 N
,
заданных парами (а,
b)
и (с,
d),
найдем пару натуральных чисел, которая
определяет их произведение. Перемножая
равенства х
= a
– b
и у = с –
d,
получаем:
ху
= (ac
+ bd)
– (ad
+ bc).
Таким
образом, произведение ху
определяете
парой натуральных чисел
N
,
заданных парами (а,
b)
и (с,
d),
найдем пару натуральных чисел, которая
определяет их произведение. Перемножая
равенства х
= a
– b
и у = с –
d,
получаем:
ху
= (ac
+ bd)
– (ad
+ bc).
Таким
образом, произведение ху
определяете
парой натуральных чисел
(ac + bd, ad + bc). (3)
Итак, если представлять натуральные числа х, у в виде разностей х = a – b, у = с – d или, что одно и то же, в виде пар натуральных чисел (а, b) и (с, d), где а > b, с > d, то их равенство, сумма, произведение определяются условиями (1), (2), (3) соответственно. Но в них над компонентами пар выполняются только операции сложения и умножения, которые всегда осуществимы во множестве натуральных чисел, а значит, условия (1), (2), (3) могут быть распространены на случай пар натуральных чисел (а, b) и (с, d), в которых а ≤ b, с≤ d.
Последним замечанием мы и будем руководствоваться при расширении множества N0 целых неотрицательных чисел до множества Z. А именно, элемент множества Z определим как совокупность пар натуральных чисел, удовлетворяющих равенству (1). Операции сложения и умножения в Z определим с помощью пар (2) и (3) соответственно. При этом будем рассматривать пары, удовлетворяющие как неравенствам а > b и с > d, так и неравенствам а ≤ b, с≤ d.
Определение 1. Две пары натуральных чисел (а, b) и (с, d) называются эквивалентными тогда и только тогда, когда a + d = b + c.
Если пары (а, b) и (с, d) эквивалентны, то будем записывать: (а, b) ~ (с, d).
Нетрудно показать, что введенное бинарное отношение на множестве пар натуральных чисел обладает следующими свойствами:
1° (а, b) ~ (а, b) – рефлексивность;
2° ((а, b) ~ (с, d)) => ((с, d) ~ (а, b)) – симметричность;
3°
(((а,
b)
~ (с,
d))
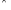 ((с,
d)
~
(e,
f)))
=> ((а,
b)
~ (e,
f))
– транзитивность.
((с,
d)
~
(e,
f)))
=> ((а,
b)
~ (e,
f))
– транзитивность.
Выполнимость свойств рефлексивности и симметричности проверяется элементарно. Докажем справедливость свойства транзитивности. По определению, эквивалентности (а, b) ~ (с, d) и (с, d) ~ (e, f) означают выполнимость следующих равенств: a + b = b + с; с + f = d + e. К обеим частям первого из этих равенств прибавим f, а к обеим частям второго – b. В результате получим равенства:
a + d + f = b + c + f; b + c + f =b + d + e.
Отсюда по транзитивности равенства натуральных чисел можем записать: a + d + f = b + d + e, или a + f = b + e, но последнее равенство означает эквивалентность пар (а, b) и (e, f).
Отношение эквивалентности, установленное на множестве пар натуральных чисел, разбивает это множество на классы попарно эквивалентных элементов. Класс, которому принадлежит пара (а, b), обозначается символом К(а, b).
Определение 2. Класс эквивалентных пар натуральных чисел называется целым числом.
2. Из определения целого числа ясно, что два числа К(а, b) и К(с, d) равны в том и только том случае, когда (а, b) ~ (с, d), то есть
(K(а,
b)
= K(с,
d))
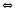 ((а,
b)
~
(с,
d)).
((а,
b)
~
(с,
d)).
Далее во множестве целых чисел введем операции сложения и умножения и покажем, что они коммутативны, ассоциативны и удовлетворяют дистрибутивному закону.
Определение 3. Суммой двух целых чисел К(а, b) и К(с, d) называется целое число К(а + с, b + d).
К(а,
b)
и
К(с,
d)
 К(а
+ с, b
+ d).
(4)
К(а
+ с, b
+ d).
(4)
Покажем, что определенная таким образом сумма не зависит от выбора представителей в классах К(а, b) и К(с, d).
Теорема
1. Если
(а1,
b1)
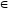 К(а,
b)
и
(с1,
d1)
К(а,
b)
и
(с1,
d1)
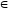 К(с,
d),
то
(а1
+ с1,
b1
+ d1)
К(с,
d),
то
(а1
+ с1,
b1
+ d1)
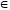 K(a
+ c,
b+d).
K(a
+ c,
b+d).
Доказательство.
Поскольку
(а1,
b1)
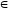 К(а,
b)
и
(с1,
d1)
К(а,
b)
и
(с1,
d1)
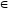 К(с,
d),
то
(а1,
b1)
~ (а,
b)
и
(с1,
d1)
~ (с,
d),
а это означает, что а1 +
b
= b1
+
а
и с1
+ d
= d1
+
c.
Складывая эти равенства почленно,
получаем а1
+ с1
+ b
+
d
= b1
+ d1
a
+ с.
Последнее равенство означает, что (а1
+ с1,
b1
+ d1)
~ (а
+ с, b
+ d),
то есть (а1
+ с1,
b1
+ d1)
К(с,
d),
то
(а1,
b1)
~ (а,
b)
и
(с1,
d1)
~ (с,
d),
а это означает, что а1 +
b
= b1
+
а
и с1
+ d
= d1
+
c.
Складывая эти равенства почленно,
получаем а1
+ с1
+ b
+
d
= b1
+ d1
a
+ с.
Последнее равенство означает, что (а1
+ с1,
b1
+ d1)
~ (а
+ с, b
+ d),
то есть (а1
+ с1,
b1
+ d1)
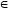 K(a
+ c,
b+d).
K(a
+ c,
b+d).
Определение 4. Произведением двух целых чисел К(а, b) и К(с, d) называется целое число К(ас + bd, ad + bc).
K(а,
b)
· K(с,
d)
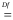 K(ac
+ bd,
ad + bc).
(5)
K(ac
+ bd,
ad + bc).
(5)
Произведение, как и сумма, не зависит от выбора пар в перемножаемых числах.
Теорема
2. Если
(а1,
b1)
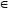 К(а,
b)
и
(с1,
d1)
К(а,
b)
и
(с1,
d1)
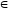 К(с,
d),
то (a1c1
+ b1d1,
a1d1
+ b1c1)
К(с,
d),
то (a1c1
+ b1d1,
a1d1
+ b1c1)
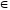 K(ac
+ bd,
ad
+ bc).
K(ac
+ bd,
ad
+ bc).
Доказательство.
Как
и в теореме 1, из того, что (а1,
b1)
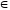 К(а,
b)
и
(с1,
d1)
К(а,
b)
и
(с1,
d1)
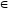 К(с,
d),
следует, что а1
+ b
= b1
+а
и с1
+ d
= d1
+с.
Первое из этих равенств умножим на с1,
после
чего, прибавив к обеим частям bd
+ a1d1
+ ad,
получим:
а1с1+b(c1
+
d)
+ a1d1
+
ad
=
b1с1
+ а(c1
+ d)
+ bd
+ a1d1.
Используя равенство
c1
+ d
= d1
+ c
и
группируя члены, находим: а1с1
+ d1(b
+ a1)
+bс
+ ad
= b1с1
+
ас
+ ad1
+
bd
+
a1d1.
Далее, учитывая равенство
b
+ а1
= а
+ b1,
будем иметь: a1c1
+ b1d1+
ad
+ bc
= а1d1
b1c1
+ ac
+bd.
Но последнее равенство означает, что
(a1c1
+ b1d1,
a1d1
+ b1c1)
~
(ac
+ bd,
ad
+ bc),
или, что одно и то же, (a1c1
+ b1d1,
a1d1
+ b1c1)
К(с,
d),
следует, что а1
+ b
= b1
+а
и с1
+ d
= d1
+с.
Первое из этих равенств умножим на с1,
после
чего, прибавив к обеим частям bd
+ a1d1
+ ad,
получим:
а1с1+b(c1
+
d)
+ a1d1
+
ad
=
b1с1
+ а(c1
+ d)
+ bd
+ a1d1.
Используя равенство
c1
+ d
= d1
+ c
и
группируя члены, находим: а1с1
+ d1(b
+ a1)
+bс
+ ad
= b1с1
+
ас
+ ad1
+
bd
+
a1d1.
Далее, учитывая равенство
b
+ а1
= а
+ b1,
будем иметь: a1c1
+ b1d1+
ad
+ bc
= а1d1
b1c1
+ ac
+bd.
Но последнее равенство означает, что
(a1c1
+ b1d1,
a1d1
+ b1c1)
~
(ac
+ bd,
ad
+ bc),
или, что одно и то же, (a1c1
+ b1d1,
a1d1
+ b1c1)
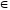 K(ac
+ bd,
ad
+ bc).
Тем самым теорема доказана.
K(ac
+ bd,
ad
+ bc).
Тем самым теорема доказана.
Поскольку в определениях операций сложения и умножения целых чисел содержатся только действия сложения и умножения натуральных чисел (см. формулы (4), (5)), то существование и единственность суммы и произведения целых чисел вытекает из существования и единственности их во множестве натуральных чисел N. Доказательства требовала только независимость суммы и произведения от выбора представителей в классах.
Операции сложения и умножения целых чисел обладают следующими свойствами:
1. К(а, b) + K(с, d) = K(с, d) + K(а, b) – коммутативность сложения;
2. (К(а, b) + K(с, d))+K(e, f) = К(а, b) +(K(с, d) + K(e, f)) – ассоциативность сложения;
3. К(а, b) · K(с, d) = K(с, d) · K(а, b) – коммутативность умножения;
4. (К(а, b) · K(с, d)) · K(e, f) = К(а, b) · (K(с, d) · K(e, f)) – ассоциативность умножения;
5. К(а, b) · (K(с, d) + К(e, f)) = K(а, b) · K(с, d) + K(а, b) · K(e, f) – дистрибутивность умножения относительно сложения.
Справедливость свойств легко проверить сравнением левой и правой частей равенств. Докажем, например, справедливость дистрибутивности.
К(а, b) · (K(с, d) + К(e, f)) = K (а, b) · K(c + е, d + f) = К(ас + ае + bd + bf, ad + af + be + be).
K(а, b) · K(с, d) + K(а, b) · K(e, f) = К(ас + bd, ad + be) + K(ae + bf, af + bе) = K(ac + bd + ае + bf, ad + bc + af + be).
Правые части полученных равенств совпадают, тем самым справедливость дистрибутивности установлена. Коммутативность и ассоциативность доказываются аналогично.
Определение 5. Разностью двух целых чисел К(а, b) и К(с, d) называется целое число К(х, у), удовлетворяющее условию К(с, d) + К(х, у) = К(а, b).
В дальнейшем будем использовать обозначение
К(х, у) = К(а, b) – K(с, d).
Действие, с помощью которого находится разность двух целых чисел, называется вычитанием.
Теорема 3. Разность любых двух целых чисел К(а, b) и K(с, d) существует и единственна.
Доказательство существования. Определим сначала вид числа К(х, у). По определению 5 разности имеем К(с, d) + К(х, у) = К(а, b). По определению 3 суммы K(c, d) + K(x, y) = К(с + х, d + y). Таким образом получаем равенство К(с + x, d + у) К(а, b). Это равенство равносильно эквивалентности (с + x, d + у) ~ (а, b), или равенству с + x + b = d + y + a. Сгруппировав слагаемые в последнем равенстве, перепишем его в виде x + (c + b) = y+ (а + d), что означает справедливость эквивалентности (x, у) ~ (а + d, b + с). Следовательно, К(х, у) = K(a + d, b + с).
Покажем теперь, что число K(a + d, b + с) является разностью чисел К(а, b) и К(с, d).
Действительно, К(с, d) + K(x, y) = К(с, d) + K(a + d, b + с) = K(c + a + d, d + b + c) = К(а + с + d, b + с + d) = K(а, b). Справедливость последнего равенства вытекает из эквивалентности (a + c + d, b +с + d) ~ (а, b).
Итак, существование разности целых чисел доказано.
Доказательство единственности. Предположим, что существуют две разности K(x, y) и K(u,v) целых чисел К(а, b) и K(с, d). Тогда справедливы равенства:
K(с, d) + K(x, y) = К(а, b); K(c, d) + K(u,v) = К(а, b).
Эти равенства можно переписать в следующем виде:
K(c + x, d + y) = K(а, b); К(с + и, d+ v) = K(а, b).
Отсюда следует, что K(c + x, d + y) = К(с + и, d+ v), а это равносильно равенству с + x + d + v = d + y + c + u, или x + v = y + u. Последнее означает, что (х, у) ~ (u ,v), то есть K(x, y) = K(u, v). Тем самым единственность доказана.
Как следует из доказательства теоремы 3, разность двух целых чисел К(а, b) и K(с, d) находится по формуле:
К(а, b) – К(с, d) = K(a + d, b + с).
Теорема
4.
Если целое число К(а,
b)
таково,
что а
=
b,
то для любой пары (с,
d)
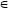 К(а,
b)
будет
с
= d.
К(а,
b)
будет
с
= d.
Если
а > b,
то для любой пары (с,
d)
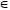 К(а,
b)
будет с
> d.
К(а,
b)
будет с
> d.
Если
а < b,
то для любой пары (с,
d)
 К(а,
b)
будет с
<
d.
К(а,
b)
будет с
<
d.
Доказательство. Пусть а = b и (с, d) – любая пара, входящая в класс К(а, а). Из (с, d) ~ (а, а) следует, что c + a = d + a и c = d.
Рассмотрим
теперь целое число К(а,
b)
такое,
что а
> b,
и
пусть (с,
d)
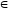 К(а,
b).
Тогда a
= b
+ k,
где k
К(а,
b).
Тогда a
= b
+ k,
где k
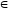 N
и
a
+ d
= b
+ c.
Подставив в последнее равенство значение
a
= b
+ k,
получим
b
+ k
+ d
= b
+ c,
или
d
+ k
= c,
что означает с
> a.
N
и
a
+ d
= b
+ c.
Подставив в последнее равенство значение
a
= b
+ k,
получим
b
+ k
+ d
= b
+ c,
или
d
+ k
= c,
что означает с
> a.
Если
а < b,
то для любой пары (с,
d)
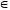 К(а,
b)
можем записать: (с,
d)
~
(а,
b)
или c
+ b
= d
+ a,
где b
= a
+ m,
m
К(а,
b)
можем записать: (с,
d)
~
(а,
b)
или c
+ b
= d
+ a,
где b
= a
+ m,
m
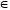 N.
Тогда
c
+ a
+ m
= d
+ a.
Отсюда следует, что с
+ m
= d,
и
значит, с
<
d.
Теорема
доказана.
N.
Тогда
c
+ a
+ m
= d
+ a.
Отсюда следует, что с
+ m
= d,
и
значит, с
<
d.
Теорема
доказана.
Определение 6. Целое число К(а, а) будем называть нулем и обозначать символом 0.
Целое число К(а, b), где а > b, будем называть целым положительным, или натуральным, числом.
Целое число К(а, b), где а < b, будем называть целым отрицательным числом.
Таким образом, множество Z целых чисел разбивается на три класса: множество натуральных чисел; множество отрицательных целых чисел, множество, состоящее из одного числа – нуля.
Натуральное число К(а + п, а) будем обозначать в дальнейшем символом n.
Теорема 5. Сумма и произведение натуральных чисел являются натуральными числами.
Доказательство. Пусть n = К(а + п, а) и m = К(b + m, b) – натуральные числа. Их сумма n + m = K(a + n, a) + К(b + m, b) = К(a + b + m + n, а + b) является натуральным числом.
Рассмотрим произведение nm = К(а + п, а) · К(b + т, b) = К((а + n)(b + m) + ab, (a + n)b + a(b + m)) = К(аb + пb + ат + пт + ab, ab + nb + ab + am) = K(2ab + nb + am + nm, 2ab + nb + am) = K(c + mn, c), здесь с = 2ab + nb + am.
Число K(c + mn, c) является натуральным, и справедливость теоремы доказана.
Определение 7. Число K(с, d) называется противоположным числу К(а, b), если К(а, b) + K(с, d) = 0.
Число противоположное К(а, b), обозначается через – К(а, b). Таким образом, знак минус, поставленный перед целым числом, означает переход к противоположному числу.
Согласно определению 7, имеем равенство: – К(а, b) + К(а, b) = К(с, с). По определению 5 разности двух целых чисел можем записать
– К(а, b) = К(с, с) – К(а, b) = К(с + b, c + a) = К(b, a).
Следовательно,
К(b,
a)
есть
число, противоположное числу К(а,
b).
В
частности, целое
отрицательное число К(a,
a
+n)
является противоположным
натуральному числу п
= К(а
+
n,
а).
Поэтому отрицательные целые числа будем
обозначать в дальнейшем
символом – n,
где п
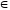 N.
N.
Определение 8. Модулем (абсолютной величиной) целого числа х называется само это число, если х – натуральное, и число – х, если х – целое отрицательное. Модуль нуля равен нулю.
Модуль
числа х
обозначается
через
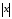 .
Используя
введенное обозначение, определение 8
можем записать в следующем виде:
.
Используя
введенное обозначение, определение 8
можем записать в следующем виде:
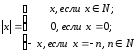
Далее рассмотрим ряд свойств целых чисел.
1) –n = (–1) · n;
2) (–1) · (–1) = 1;
3) – (–n) = n;
4) (–п) · (–m) = n · m;
5) (–п) · т = – п · т;
6) n – m = n + (–т) = –(m – n);
7) (–n) + (–m) = –(n + m);
8) –0 = 0.
Докажем, например, справедливость свойств 1 и 4. По определению, –1 = К(а, a + 1), n = К(b + n, b). Тогда (–1) · п = К(а, a + 1) · К(b + n, b) = K(a(b + n) + b(a + 1), ab + (a + 1)(b + n)) = K(2ab + an + b, 2ab + an + b + n) = K(c, с + п) = –п.
Здесь с = 2ab + an + b. Тем самым доказано, что (–1) · п = – n.
Справедливость свойства 4 вытекает из свойств 1 и 2, так как (–n) · (–m) = (–1) · n · (–1) · m = (–1) · (–1) · п · т = 1 · n · m = п · т. Остальные свойства доказываются аналогично.
В дальнейшем будем говорить, что натуральное число имеет знак плюс (+), а отрицательное – знак минус (–).
Из свойств 1 – 8 легко выводятся правила сложения и умножения целых чисел.
Правило сложения. При сложении двух целых чисел с одинаковыми знаками получается число того же знака, модуль которого равен сумме модулей слагаемых.
При сложении чисел с разными знаками получается число, знак которого совпадает со знаком слагаемого, имеющего больший модуль, а модуль равен разности модулей слагаемых.
Сумма противоположных чисел равна нулю, а сложение с нулем не меняет числа.
Правило умножения. При умножении двух целых чисел получается число, модуль которого равен произведению модулей множителей, а знак положителен, если знаки множителей одинаковы, и отрицателен, если множители имеют противоположные знаки.
Если хотя бы один из множителей равен нулю, то произведение равно нулю.
