
gosy_voprosy / вопрос_49
.docxВероятностная модель — матмодель реального явления, содержащего элементы случайности(т. е., принципиально неустранимой неопределённости).
Стохастическая ситуация — ситуация, обладающая свойствами:
-
Наличие случайности (неопределённости).
-
Воспроизводимость с учётом случайности.
-
Устойчивость частот событий
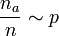 ,
где
,
где
![]() —
число
экспериментов, в которых произошло
событие A,
—
число
экспериментов, в которых произошло
событие A,
![]() —
общее
число экспериментов,
—
общее
число экспериментов,
![]()
Вероятностное
пространство
— тройка
![]() .
.
![]() —
произвольное
непустое
множество.
—
произвольное
непустое
множество.
![]() называют
элементарными
исходами.
называют
элементарными
исходами.
![]() —
—
![]() -алгебра
подмножеств
-алгебра
подмножеств
![]() .
.
![]() называют
событиями.
называют
событиями.
![]() —
вероятность,
которая должна обладать указанными
ниже свойствами.
—
вероятность,
которая должна обладать указанными
ниже свойствами.
Свойства вероятности
-
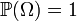 .
.
-
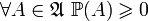 .
.
-

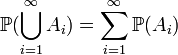 (счётная
аддитивность).
(счётная
аддитивность).
Семейство
![]() подмножеств
подмножеств
![]() является
является
![]() -алгеброй:
-алгеброй:
-
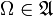 .
.
-
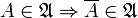 .
.
-
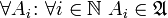
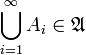 .
.
![]() —
борелевская
—
борелевская
![]() -алгебра,
порождённая всеми множествами вида
-алгебра,
порождённая всеми множествами вида
![]()
Парадокс БертранаПравить
Какова вероятность того, что длина произвольной хорды внутри окружности превосходит длину стороны правильного вписанного треугольника?
-
 Фиксируем
начало хорды в одной из вершин, все
хорды внутри угла
Фиксируем
начало хорды в одной из вершин, все
хорды внутри угла
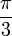 подходят.
подходят.
-
 Любая
из хорд с серединой внутри вписанной
в этот треугольник окружности
Любая
из хорд с серединой внутри вписанной
в этот треугольник окружности
-
 Любая
из перпендикулярных диаметру хорд,
пересекающая его не дальше, чем R/2 от
центра окружности.
Любая
из перпендикулярных диаметру хорд,
пересекающая его не дальше, чем R/2 от
центра окружности.
А
всё потому, что в постановке задачи не
оговорено
![]() ,
а сказано только «произвольно выбранная».
Итого, правильный ответ — любое число
от 0 до 1.
,
а сказано только «произвольно выбранная».
Итого, правильный ответ — любое число
от 0 до 1.
МОНТЕ-КАРЛО МЕТОД
(метод статистических испытаний) - численный метод решения разл. задач при помощи моделирования случайных событий. В приложении к физике M.-К. м. можно определить как метод исследования физ. процесса путём создания и эксплуатации стохастич. модели, отражающей динамику данного процесса.
Если физ. процесс описывается k величинами (переменными) p1,...,pk, к-рые можно рассматривать как случайные величины с плотностью распределения F(p1,....,pk), и требуется оценить плотность распределения нек-рой характеристики f данного процесса, являющейся ф-цией переменных, f= f(p1,...,pk), или совокупности таких характеристик f1,...,fm, то M.-К. м. состоит в следующем. Создаётся алгоритм, реализуемый в виде программы на ЭВМ или в виде спец. устройства (электронного, механического или др.). Назначение алгоритма - многократно генерировать набор величин q1,...,qk. с плотностью вероятности F. Процедуру многократного получения набора {qj} наз. моделированием физ. процесса; числа qj отождествляют с переменными pj. Для каждого конкретного набора {qji}вычисляют величину f(qi1,...,qik); получив достаточно большое число N наборов {qj}, можно оценить ср. значение величины f, её дисперсию и поведение ф-ции распределения плотности вероятности. Такой подход наз. прямым моделированием. При т. н. косвенном моделировании процесс описывают одним или неск. ур-ниями (дифференц., интегральными или др.), к-рые решают затем с помощью M.-К. м. С матем. точки зрения обе процедуры эквивалентны вычислению интеграла по нек-рой многомерной области. Кратность вычисляемого интеграла варьируется от 10-20 (в нек-рых задачах физики элементарных частиц) до ~106 (в расчётах на решётке).
M.-К. м. был сформулирован в 1949 в работах Дж. Неймана (J. Neumann), С. Улама (S. Ulam), H. Метрополиса (N. Metropolis). Предшественник M.-К. м. - статистическое моделирование, известное ещё в 19 в. Классич. примером такого моделирования является "игла Бюффона", т. е. получение числа p путём случайного бросания иглы на горизонтальную поверхность, расчерченную сеткой равноотстоящих параллельных линий. С появлением быстродействующих компьютеров метод обрёл второе рождение и получил в 1949 назв. "метод Монте-Карло".
Техника моделирования. Обычно M.-К. м. реализуют в виде программы на универсальной ЭВМ. Ранее применялись механич. устройства, ныне всё чаще используют спец. моделирующие устройства с применением микропроцессоров. С помощью таких устройств получен ряд результатов в статистич. физике и квантовой теории поля.
Для реализации случайной величины в M.-К. м. традиционно используют датчики, генерирующие случайную последовательность чисел, равномерно распределённых на интервале (0,1). Различают три типа случайных чисел. Истинно случайные числа можно вырабатывать, напр., преобразуя случайные сигналы от радиоакт. источника или от шумового диода. Таким способом можно достаточно быстро получать большие последовательности некоррелированных случайных чисел. В расчётах на ЭВМ используют псевдослучайные числа, полученные с помощью нек-рого алгоритма. Назначение такого алгоритма - генерировать числа, к-рые похожи на случайные, хотя, строго говоря, они детерминированы. Необходимы спец. исследования и тесты, чтобы убедиться в достаточной случайности таких чисел (равномерность распределения, отсутствие корреляций и пр.). Квазислучайные числа также получают при помощи нек-рого алгоритма, причём в основу алгоритма закладывают требование равномерного заполнения точками заданного многомерного объёма. Известен ряд алгоритмов, дающих точки, распределённые в гиперкубе более равномерно, чем случайные и псевдослучайные. Следствием лучшей равномерности является более быстрая сходимость результата.
Использование
M.-К. м. в физике базируется гл. обр. на
возможности его применения для вычисления
интегралов, решения интегральных ур-ний
и др. Пусть требуется вычислить интеграл
![]() ,
где W - конечная k
-мерная область определения. Алгоритм
вычисления в M.-К. м. основан на теореме
о среднем:
,
где W - конечная k
-мерная область определения. Алгоритм
вычисления в M.-К. м. основан на теореме
о среднем:
![]() ,
где V
-
объём области W. Выберем k
-мерный параллелепипед с объёмом W,
содержащий область W, и выберем случайным
образом достаточно большое число N
точек, равномерно распределённых в этом
параллелепипеде. Для M
точек, попавших при этом в область W,
вычислим значение ф-ции f.
Оценку интеграла даёт величина
,
где V
-
объём области W. Выберем k
-мерный параллелепипед с объёмом W,
содержащий область W, и выберем случайным
образом достаточно большое число N
точек, равномерно распределённых в этом
параллелепипеде. Для M
точек, попавших при этом в область W,
вычислим значение ф-ции f.
Оценку интеграла даёт величина
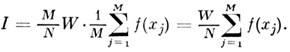
Если в области W точки распределены с плотностью вероятности р(х), то, зная объём V, можно получить след. оценку интеграла:
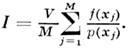
Алгоритм решения интегрального ур-ния
![]()
M.-К. м. таков. Для достаточно широкого класса ядер К(х, <у )приближённое решение можно искать в виде суммы
![]()
где
![]()
Пусть далее нам нужно найти функционал
![]()
Построим стохастич. процесс, соблюдая след. правила. Будем многократно строить цепочки из M случайных точек. Первая точка x0 всегда "бросается" в область W с плотностью вероятности f(x )(с точностью до нормирующего множителя); переход от точки xm-1 к точке х т определяется плотностью вероятности К(х т-1, xm)dxm. Можно показать, что матем. ожидание
случайной
величины
 равно
искомому функционалу Ф. Вообще говоря,
можно осуществлять переход xm-1->
х
т
спроизвольной
плотностью вероятности P(xm-1,xm)dxm.
При
этом случайная величина, с помощью к-рой
оценивается функционал, вычисляется
по ф-ле
равно
искомому функционалу Ф. Вообще говоря,
можно осуществлять переход xm-1->
х
т
спроизвольной
плотностью вероятности P(xm-1,xm)dxm.
При
этом случайная величина, с помощью к-рой
оценивается функционал, вычисляется
по ф-ле
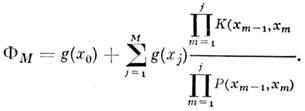
При моделировании физ. процесса важно выбрать оптим. ф-цию р(х)[или Р(х т-1,х т)]. Разработке методов, позволяющих правильно выбрать эти ф-ции, посвящено большинство работ, связанных с вопросом ускорения сходимости. Перспективным является, напр., адаптивный метод, при к-ром ф-ция р(х)"настраивается" в процессе моделирования на данную подынтегральную ф-цию f(x).
Структура и классификация СМО
Системы
массового обслуживания
– это такие системы, которые обслуживают
массовый поток требований, при этом
поток требований является случайной
величиной.
В простейшем случае СМО
может быть представлена в виде условной
схемы, где изображены ее составные
части.
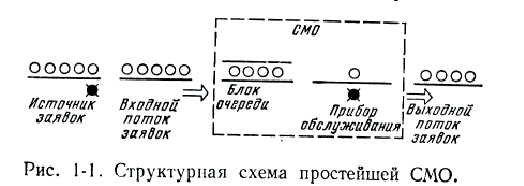 На
этой схеме представлен источник заявок,
который формирует входной поток,
задерживая на какой-то отрезок времени
поступление заявки в его состав. Заявки
условно представлены шариками. Интервалы
между заявками входного потока в общем
случае неодинаковы: они представляют
собой случайные величины и определяются
вероятностными законами входного
потока. Заявки поступают на вход блока
очереди, в которой реализуется заданный
закон дисциплины очереди. Этот закон
определяет порядок обслуживания входных
заявок (или их поступления на обслуживание),
который может быть детерминированным
(например, первой обслуживается та
заявка, которая первой поступила, или
первой обслуживается последняя
поступившая заявка) или случайным
(например, в соответствии с законом
Эрланга).
Прибор обслуживания
осуществляет обслуживание каждой
поступившей на его вход заявки в
соответствии с заданным детерминированным
или случайным законом обслуживания.
Обслуженная заявка поступает в выходной
поток, который отличается от входного
потока в зависимости от законов дисциплины
очереди и обслуживания. Таким образом,
в состав СМО входят два блока: блок
очереди и прибор обслуживания.
Для
модели СМО характерно, что все явления
описываются с помощью событий, которые
появляются в тот или иной момент времени
(на временной оси). Входной поток заявок
– это временная последовательность
событий на входе СМО, для которой
появление события (заявки) подчиняется
вероятностным (или детерминированным)
законам. Блок дисциплины очереди в
соответствии с заданным вероятностным
(или детерминированным) законом
осуществляет выборку (или перераспределение)
во времени (или на временной оси) событий
во входном потоке для выдачи их на вход
прибора обслуживания. Последний согласно
своему закону осуществляет задержку
во времени каждого поступающего на его
вход события и формирует выходной поток
заявок СМО. Идеализация модели СМО
заключается в том, что все остальные
свойства реальных систем, которые не
вписываются в эту модель событий, не
учитываются.
Примерами реальных
систем управления, которые сводятся к
моделям СМО, могут служить системы
управления аэропортом, телефонной сетью
большого города. При этом поток
воздействий – случайная величина, так
как интервалы между вылетами и посадкой
самолетов, между вызовами абонентами
телефонной станции, поступлениями
заявок клиентов на обслуживание в сети
бытового обслуживания и т.д. представляет
собой случайные величины. Кроме того,
время обслуживания самолета, разговора
по телефону и обслуживания в предприятии
бытового обслуживания также является
случайной величиной.
На
этой схеме представлен источник заявок,
который формирует входной поток,
задерживая на какой-то отрезок времени
поступление заявки в его состав. Заявки
условно представлены шариками. Интервалы
между заявками входного потока в общем
случае неодинаковы: они представляют
собой случайные величины и определяются
вероятностными законами входного
потока. Заявки поступают на вход блока
очереди, в которой реализуется заданный
закон дисциплины очереди. Этот закон
определяет порядок обслуживания входных
заявок (или их поступления на обслуживание),
который может быть детерминированным
(например, первой обслуживается та
заявка, которая первой поступила, или
первой обслуживается последняя
поступившая заявка) или случайным
(например, в соответствии с законом
Эрланга).
Прибор обслуживания
осуществляет обслуживание каждой
поступившей на его вход заявки в
соответствии с заданным детерминированным
или случайным законом обслуживания.
Обслуженная заявка поступает в выходной
поток, который отличается от входного
потока в зависимости от законов дисциплины
очереди и обслуживания. Таким образом,
в состав СМО входят два блока: блок
очереди и прибор обслуживания.
Для
модели СМО характерно, что все явления
описываются с помощью событий, которые
появляются в тот или иной момент времени
(на временной оси). Входной поток заявок
– это временная последовательность
событий на входе СМО, для которой
появление события (заявки) подчиняется
вероятностным (или детерминированным)
законам. Блок дисциплины очереди в
соответствии с заданным вероятностным
(или детерминированным) законом
осуществляет выборку (или перераспределение)
во времени (или на временной оси) событий
во входном потоке для выдачи их на вход
прибора обслуживания. Последний согласно
своему закону осуществляет задержку
во времени каждого поступающего на его
вход события и формирует выходной поток
заявок СМО. Идеализация модели СМО
заключается в том, что все остальные
свойства реальных систем, которые не
вписываются в эту модель событий, не
учитываются.
Примерами реальных
систем управления, которые сводятся к
моделям СМО, могут служить системы
управления аэропортом, телефонной сетью
большого города. При этом поток
воздействий – случайная величина, так
как интервалы между вылетами и посадкой
самолетов, между вызовами абонентами
телефонной станции, поступлениями
заявок клиентов на обслуживание в сети
бытового обслуживания и т.д. представляет
собой случайные величины. Кроме того,
время обслуживания самолета, разговора
по телефону и обслуживания в предприятии
бытового обслуживания также является
случайной величиной.
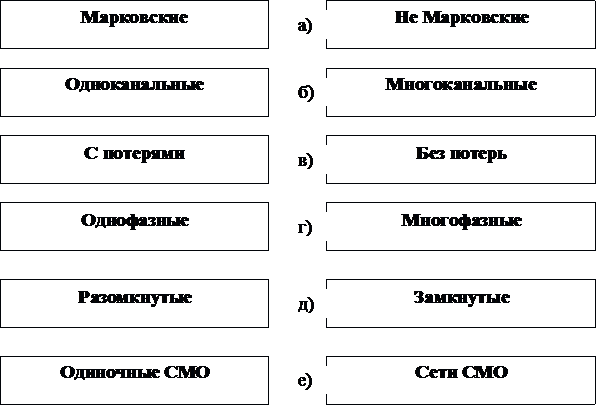 Существует
большое количество различных моделей
СМО и методов их классификации.
Существует
большое количество различных моделей
СМО и методов их классификации.
Рис. Классификация СМО
Прежде всего, они разделяются на Марковские и не Марковские. СМО относятся к Марковским системам, если они описываются с помощью дискретных Марковских цепей. Аналитическому исследованию поддаются только частные случаи нелинейных СМО, которые выделяются в отдельные классы полумарковских, линейчатых и других СМО. Далее СМО классифицируют на одноканальные и многоканальные в зависимости от числа приборов обслуживания, которые могут одновременно обслуживать входные заявки. При этом входной поток может быть один или их может быть несколько. Системы массового обслуживания делятся на два типа: системы обслуживания с потерями и системы обслуживания без потерь. Системы массового обслуживания с потерями – это такие системы массового обслуживания, в которых система отвечает отказом требованию, которое поступило в такой момент, когда все обслуживающие аппараты занятые, таким образом полностью отсутствуют условия для образования очереди. Системы массового обслуживания без потерь – это такие системы, в которых требование, которое поступило, будет находиться в системе до тех пор, пока не закончится ее обслуживание. Система массового обслуживания без потерь имеет большое количество разновидностей, определяемых различными законами ожидания в очереди, дисциплиной очереди. Для исследования последовательного процесса обслуживания несколькими приборами введена модель многофазной СМО, в которой заявка после обслуживания одним прибором поступает на следующий. Далее можно ввести понятия разомкнутой и замкнутой СМО, в которой обслуженная заявка снова поступает на обслуживание. В современных системах управления встречаются такие сложные комбинации всех рассмотренных выше СМО, что они образуют целую сеть СМО.
Примеры СМО в металлургической промышленности Примерами систем массового обслуживания без потерь в металлургической промышленности являются производственные системы металлургических цехов. Производственные процессы в металлургических цехах должны быть организованы таким образом, чтобы производство было максимально эффективным. Неэффективность производства приводит к большим экономическим потерям. Для обеспечения эффективной работы производственных мощностей необходимо правильно выбрать их параметры. Параметры должны выбираться таким образом, чтобы мощности могли обслуживать случайный поток требований. Этим вопросом "занимается" теория массового обслуживания. Примерами систем массового обслуживания в металлургии являются:
-
Система шихтоподачи. Разные виды шихты (агломерат, кокс и др.), которые засыпаются в доменную печь, являются потоком требований. Система шихтоподачи должна обеспечивать своевременная загрузку доменной печи шихтой с целью поддержания нужного вида засыпи. Загрузка в системах шихтоподачи может производиться либо двумя скипами, либо конвейером для доменных печей большого объема. В первом случае – это многоканальная (а точнее двухканальная СМО), а во втором – одноканальная.
-
Система подачи лома и чугуна в конвертор. Потребность сталеплавильного агрегата в этих материалах является потоком требований. Система подачи материалов должна обеспечить своевременную их загрузку в конвертор. Многоканальная СМО.
-
Машина непрерывного литья заготовок. Здесь потоком требований являются ковши со сталью, которые нужно разлить. Очень важным является правильный выбор количества МНЛЗ. Количество МНЛЗ рассчитывают, исходя из того, чтобы при работе методом "плавка на плавку" была обеспеченная синхронность работы машин непрерывного литья заготовок и сталеплавильных агрегатов. Многоканальная СМО.
-
Комплекс ковшового вакуумирования. Ковши со сталью являются потоком требований. Одноканальная, многофазная СМО (МСШ, установка "печь-ковш", вакуумная камера).
Потоки
заявок в СМО
Потоки
заявок бывают входные и выходные.
Входной
поток заявок – это временная
последовательность событий на входе
СМО, для которой появление события
(заявки) подчиняется вероятностным (или
детерминированным) законам. Если
требования на обслуживание приходят в
соответствие, с каким – либо графиком
(например, автомобили приезжают на АЗС
каждые 3 минуты) то такой поток подчиняется
детерминированным (определенным)
законам. Но, как правило, поступление
заявок подчиняется случайным законам.
Для описания случайных законов в
теории массового обслуживания вводится
в рассмотрение модель
потоков событий.
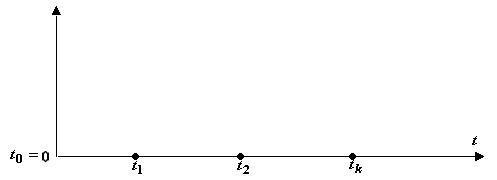
Потоком
событий
называется последовательность событий,
следующих одно за другим в случайные
моменты времени
![]() .
В
качестве событий могут фигурировать
поступление заявок на вход СМО (на вход
блока очереди), появление заявок на
входе прибора обслуживания (на выходе
блока очереди) и появление обслуженных
заявок на выходе СМО.
.
В
качестве событий могут фигурировать
поступление заявок на вход СМО (на вход
блока очереди), появление заявок на
входе прибора обслуживания (на выходе
блока очереди) и появление обслуженных
заявок на выходе СМО.
 Потоки
событий обладают различными свойствами,
которые позволяют различать различные
типы потоков. Прежде всего, потоки могут
быть однородными
и неоднородными.
Однородные
потоки – такие потоки, в которых поток
требований обладает одинаковыми
свойствами: имеют приоритет первым
пришел – первым обслужен, обрабатываемые
требования имеют одинаковые физические
свойства.
Неоднородные
потоки – такие потоки, в которых
требования обладают неодинаковыми
свойствами: требования удовлетворяются
по принципу приоритетности (пример,
карта прерываний в ЭВМ), обрабатываемые
требования имеют различные физические
свойства.
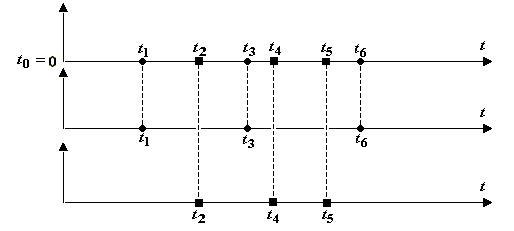
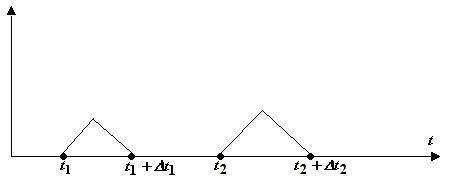
Схематично неоднородный
поток событий может быть изображен
следующим образом
Потоки
событий обладают различными свойствами,
которые позволяют различать различные
типы потоков. Прежде всего, потоки могут
быть однородными
и неоднородными.
Однородные
потоки – такие потоки, в которых поток
требований обладает одинаковыми
свойствами: имеют приоритет первым
пришел – первым обслужен, обрабатываемые
требования имеют одинаковые физические
свойства.
Неоднородные
потоки – такие потоки, в которых
требования обладают неодинаковыми
свойствами: требования удовлетворяются
по принципу приоритетности (пример,
карта прерываний в ЭВМ), обрабатываемые
требования имеют различные физические
свойства.
Схематично неоднородный
поток событий может быть изображен
следующим образом
 Соответственно
можно использовать несколько моделей
СМО для обслуживания неоднородных
потоков: одноканальная СМО с дисциплиной
очереди, учитывающей приоритеты
неоднородных заявок, и многоканальная
СМО с индивидуальным каналом для каждого
типа заявок.
Регулярным
потоком называется поток, в котором
события следуют одно за другим через
одинаковые промежутки времени. Если
обозначить через
Соответственно
можно использовать несколько моделей
СМО для обслуживания неоднородных
потоков: одноканальная СМО с дисциплиной
очереди, учитывающей приоритеты
неоднородных заявок, и многоканальная
СМО с индивидуальным каналом для каждого
типа заявок.
Регулярным
потоком называется поток, в котором
события следуют одно за другим через
одинаковые промежутки времени. Если
обозначить через
![]() –
моменты появления событий, причем
–
моменты появления событий, причем
![]() ,
а через
,
а через
![]() интервалы
между событиями, то для регулярного
потока
интервалы
между событиями, то для регулярного
потока
![]() Рекуррентный
поток
соответственно определяется как поток,
для которого все функции распределения
интервалов между заявками
Рекуррентный
поток
соответственно определяется как поток,
для которого все функции распределения
интервалов между заявками
![]() совпадают,
то есть
совпадают,
то есть
![]() Физически
рекуррентный поток представляет собой
такую последовательность событий, для
которой все интервалы между событиями
как бы "ведут себя" одинаково, т.е.
подчиняются одному и тому же закону
распределения. Таким образом, можно
исследовать только один какой-нибудь
интервал и получить статистические
характеристики, которые будут справедливы
для всех остальных интервалов.
Для
характеристики потоков очень часто
вводят в рассмотрение вероятность
распределения числа событий в заданном
интервале времени
Физически
рекуррентный поток представляет собой
такую последовательность событий, для
которой все интервалы между событиями
как бы "ведут себя" одинаково, т.е.
подчиняются одному и тому же закону
распределения. Таким образом, можно
исследовать только один какой-нибудь
интервал и получить статистические
характеристики, которые будут справедливы
для всех остальных интервалов.
Для
характеристики потоков очень часто
вводят в рассмотрение вероятность
распределения числа событий в заданном
интервале времени
![]() ,
которая определяется следующим
образом:
,
которая определяется следующим
образом:
![]() где
где
![]() –
число событий, появляющихся на интервале
–
число событий, появляющихся на интервале
![]() .
Поток
без последействия характеризуется тем
свойством, что для двух непересекающихся
интервалов времени
.
Поток
без последействия характеризуется тем
свойством, что для двух непересекающихся
интервалов времени
![]() и
и
![]()
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() ,
вероятность появления числа событий
на втором интервале не зависит от числа
появления событий на первом
интервале.
,
вероятность появления числа событий
на втором интервале не зависит от числа
появления событий на первом
интервале.
 Отсутствие
последействия означает отсутствие
вероятностной зависимости последующего
течения процесса от предыдущего. Если
имеется одноканальная СМО с временем
обслуживания
Отсутствие
последействия означает отсутствие
вероятностной зависимости последующего
течения процесса от предыдущего. Если
имеется одноканальная СМО с временем
обслуживания
![]() ,
то при потоке заявок без последействия
на входе системы выходной поток будет
с последействием, так как заявки на
выходе СМО не появляются чаще чем
интервал
,
то при потоке заявок без последействия
на входе системы выходной поток будет
с последействием, так как заявки на
выходе СМО не появляются чаще чем
интервал
![]() .
В регулярном потоке, в котором события
следуют друг за другом через определенные
промежутки времени, имеется самое
жесткое последействие.
Потоком
с ограниченным последействием
называется такой поток, для которого
интервалы
.
В регулярном потоке, в котором события
следуют друг за другом через определенные
промежутки времени, имеется самое
жесткое последействие.
Потоком
с ограниченным последействием
называется такой поток, для которого
интервалы
![]() между
событиями независимы.
Поток называется
стационарным,
если вероятность появления какого-то
числа событий на интервале времени
между
событиями независимы.
Поток называется
стационарным,
если вероятность появления какого-то
числа событий на интервале времени
![]() зависит
только от длины этого интервала и не
зависит от его расположения на оси
времени. Для стационарного потока
событий среднее число событий в единицу
времени постоянно.
Ординарным
потоком
называется такой поток, для которого
вероятность попадания на данный малый
отрезок времени dt
двух и более требований пренебрежительно
мала по сравнению с вероятностью
попадания одного требования.
Поток,
который обладает свойствами стационарности,
отсутствия последействия и ординарности
называют пуассоновским
(простейшим). Этот поток занимает
центральное место среди всего многообразия
потоков, так же как случайные величины
или процессы с нормальным законом
распределения в прикладной теории
вероятности.
Пуассоновский поток
описывается следующей формулой:
зависит
только от длины этого интервала и не
зависит от его расположения на оси
времени. Для стационарного потока
событий среднее число событий в единицу
времени постоянно.
Ординарным
потоком
называется такой поток, для которого
вероятность попадания на данный малый
отрезок времени dt
двух и более требований пренебрежительно
мала по сравнению с вероятностью
попадания одного требования.
Поток,
который обладает свойствами стационарности,
отсутствия последействия и ординарности
называют пуассоновским
(простейшим). Этот поток занимает
центральное место среди всего многообразия
потоков, так же как случайные величины
или процессы с нормальным законом
распределения в прикладной теории
вероятности.
Пуассоновский поток
описывается следующей формулой:
 ,
где
,
где
![]() –
вероятность появления
–
вероятность появления
![]() событий
за время
событий
за время
![]() ,
,
![]() –
интенсивность потока.
Интенсивностью
потока
–
интенсивность потока.
Интенсивностью
потока
![]() называют
среднее число событий, которые появляются
за единицу времени.
Математическое
ожидание и дисперсия пуассоновского
потока находится из следующих
соотношений:
называют
среднее число событий, которые появляются
за единицу времени.
Математическое
ожидание и дисперсия пуассоновского
потока находится из следующих
соотношений:
![]()
![]() Для
пуассоновского потока интервалы времени
между заявками распределены по
экспоненциальному закону
Для
пуассоновского потока интервалы времени
между заявками распределены по
экспоненциальному закону
![]() Потоком
с ограниченным последействием,
для которого интервалы времени между
заявками распределены по нормальному
закону, называется нормальным потоком.
Потоком
с ограниченным последействием,
для которого интервалы времени между
заявками распределены по нормальному
закону, называется нормальным потоком.
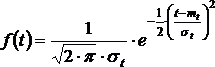
Естественным
дальнейшим обобщением Марковских
потоков (или вообще Марковских систем)
являются полумарковские
потоки,
в которых отдельно и независимо задается
матрица
![]() вероятностей
переходов из состояния
вероятностей
переходов из состояния
![]() в
состояние
в
состояние
![]() и
матрица
и
матрица
![]()
![]() вероятностей
интервалов между событиями
вероятностей
интервалов между событиями
![]() и
и
![]() .
В
частном случае
.
В
частном случае
![]() получаем
простейший поток.
получаем
простейший поток.
Законы
обслуживания
Режим
обслуживания (время обслуживания), так
же как и режим поступления заявок, может
быть либо постоянным, либо случайным.
Во многих случаях время обслуживания
подчиняется экспоненциальному
распределению.
Вероятность того, что
обслуживание закончится до момента t,
равна:
![]()
![]() где
где
![]() –
плотность потока заявок
Откуда
плотность распределения времени
обслуживания
–
плотность потока заявок
Откуда
плотность распределения времени
обслуживания
![]() Дальнейшим
обобщением экспоненциального закона
обслуживания может служить закон
распределения Эрланга, когда каждый
интервал обслуживания подчиняется
закону:
Дальнейшим
обобщением экспоненциального закона
обслуживания может служить закон
распределения Эрланга, когда каждый
интервал обслуживания подчиняется
закону:
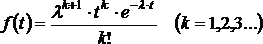 где
где
![]() –
интенсивность исходного пуассоновского
потока, k
– порядок потока Эрланга.
–
интенсивность исходного пуассоновского
потока, k
– порядок потока Эрланга.
