gosy_voprosy / вопрос _20
.docxКритерии устойчивости
[править] Критерий Рауса
Основная статья: Критерий устойчивости Рауса
Для определения устойчивости системы строятся таблицы вида:
|
Коэффициенты |
Строки |
столбец 1 |
столбец 2 |
столбец 3 |
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
Для устойчивости системы необходимо, чтобы все элементы первого столбца имели положительные значения; если в первом столбце присутствуют отрицательные элементы — система неустойчива; если хотя бы один элемент равен нулю, а остальные положительны, то система на границе устойчивости.
[править] Критерий Гурвица
Основная статья: Критерий устойчивости Гурвица
![]()
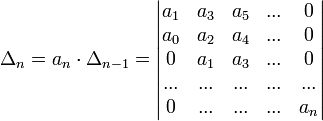 —
Определитель
Гурвица
—
Определитель
Гурвица
Теорема:
Для устойчивости замкнутой САУ необходимо
и достаточно, чтобы определитель Гурвица
и все его миноры были положительны при
![]()
[править] Критерий Михайлова
![]()
Заменим
![]() ,
где ω — угловая частота колебаний,
соответствующих чисто мнимому корню
данного характеристического полинома.
,
где ω — угловая частота колебаний,
соответствующих чисто мнимому корню
данного характеристического полинома.
![]()
![]()
![]()
Критерий:
для устойчивости линейной системы n-го
порядка необходимо и достаточно, чтобы
кривая Михайлова, построенная в
координатах
![]() ,
проходила последовательно через n
квадрантов.
,
проходила последовательно через n
квадрантов.
![]()
![]()
Рассмотрим зависимость между кривой Михайлова и знаками его корней (α>0 и β>0)
1)
Корень характеристического уравнения —
отрицательное вещественное число
![]()
Соответствующий
данному корню сомножитель
![]()
![]()
2)
Корень характеристического уравнения —
положительное вещественное число
![]()
Соответствующий
данному корню сомножитель
![]()
![]()
3)
Корень характеристического уравнения —
комплексная пара чисел с отрицательной
вещественной частью
![]()
Соответствующий
данному корню сомножитель
![]()
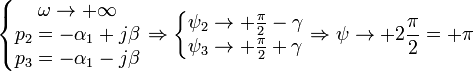 ,
где
,
где
![]()
4)
Корень характеристического уравнения —
комплексная пара чисел с положительной
вещественной частью
![]()
Соответствующий
данному корню сомножитель
![]()
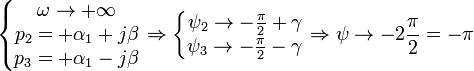 ,
где
,
где
![]()
[править] Критерий Найквиста
Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой или логарифмических частотных характеристик разомкнутой системы.
Пусть
разомкнутая система представлена в
виде полинома
![]()
тогда
сделаем подстановку
![]() и
получим:
и
получим:
![]()
Для
более удобного построения годографа
при n>2 приведём уравнение (*) к
«стандартному» виду:
![]()
При таком представлении модуль A(ω) = | W(jω)| равен отношению модулей числителя и знаменателя, а аргумент (фаза) ψ(ω) — разности их аргументов. В свою очередь, модуль произведения комплексных чисел равен произведению модулей, а аргумент — сумме аргументов.
Модули и аргументы, соответствующие сомножителям передаточной функции
|
Сомножитель |
|
|
|
k |
k |
0 |
|
p |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После
чего построим годограф для вспомогательной
функции
![]() ,
для чего будем изменять
,
для чего будем изменять
![]()
При
![]() ,
а при
,
а при
![]() (так
как n<m и
(так
как n<m и
![]() )
)
Для
определения результирующего угла
поворота найдём разность аргументов
числителя
![]() и
знаменателя
и
знаменателя
![]()
Полином
числителя вспомогательной функции
имеет ту же степень, что и полином её
знаменателя, откуда следует
![]() ,
следовательно, результирующий угол
поворота вспомогательной функции равен
0. Это означает, что для устойчивости
замкнутой системы годограф вектора
вспомогательной функции не должен
охватывать начало координат, а годограф
функции
,
следовательно, результирующий угол
поворота вспомогательной функции равен
0. Это означает, что для устойчивости
замкнутой системы годограф вектора
вспомогательной функции не должен
охватывать начало координат, а годограф
функции
![]() ,
соответственно, точку с координатами
,
соответственно, точку с координатами
![]()