
- •Глава 1. Матрицы и определители
- •§1. Матрицы и их виды
- •§2. Определители 2, 3 и n-го порядка
- •§3. Действия над матрицами
- •2 Способ (с помощью элементарных преобразований):
- •§5. Ранг матрицы.
- •§6.Формулы Крамера
- •§7. Метод Гаусса
- •§8. Матричный метод решения систем линейных уравнений
- •§10.1 Линейная зависимость векторов
- •§10.2 Базис и размерность линейного векторного пространства
- •§11.1 Скалярное произведение двух векторов в r2 и r3
- •§11.2 Скалярное произведение двух n-мерных векторов. Евклидово пространство
- •§12. Линейные операторы
- •Алгебра линейных операторов
- •§13. Собственные векторы и собственные числа линейного оператора
- •Часть 2. Элементы аналитической геометрии
- •§1. Понятие уравнения линии. Составление уравнения линии
- •§2.Уравнение прямой с угловым коэффициентом
- •§8Расстояние от точки до прямой
- •§14Гипербола
- •§15Парабола
- •§16Приведение квадратичных форм к каноническому виду
- •§17Приведение общего уравнения кривой 2-го порядка к каноническому виду
- •§18.Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •§19Общее уравнение плоскости
- •§20 Взаимное расположение двух плоскостей
- •§21 Нахождение координат любой точки, принадлежащей данной плоскости.
- •22Прямая в пространстве
- •§23Угол между прямыми в пространстве
- •Условия параллельности и перпендикулярности
Глава 1. Матрицы и определители
§1. Матрицы и их виды
Матрица обозначается заглавными латинскими буквами (А, В, С,...).
Определение
1. Прямоугольная
таблица вида
 ,
,

состоящая из m строк и n столбцов, называется матрицей.
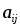 - элемент матрицы,
i
– номер строки, j
– номер столбца.
- элемент матрицы,
i
– номер строки, j
– номер столбца.
Виды матриц:
Величина
 называетсяразмерностью
матрицы
называетсяразмерностью
матрицы
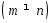 .
.Если
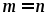 ,
матрица называетсяквадратной,
ее размерность n.
,
матрица называетсяквадратной,
ее размерность n.Если все элементы матрицы нули, то матрица называется нулевой.
Матрица вида:
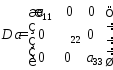 ,
называетсядиагональной.
,
называетсядиагональной.Матрица вида:
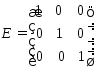 ,
называетсяединичной.
,
называетсяединичной.
Матрица вида:
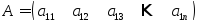 ,
называетсяматрица-строка.
,
называетсяматрица-строка.Матрица вида:
 ,
называетсяматрица-столбец.
,
называетсяматрица-столбец.Следом trA квадратной матрицы А называется сумма её
элементов, стоящих на главной диагонали:
trA=a11+a22+a33+…+ann.
§2. Определители 2, 3 и n-го порядка
Пусть даны две квадратные матрицы:

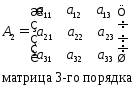
Определение
1.
Определителем второго порядка матрицы
А1
называется число, обозначаемое ∆ и
равное
 ,
где
,
где
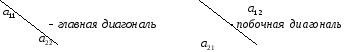
Пример. Вычислить определитель 2-го порядка:
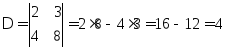
Определение 2. Определителем 3-го порядка квадратной матрицы А2 называется число вида:
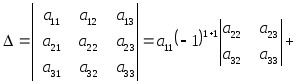
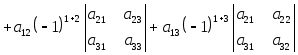
Это один из способов вычисления определителя.
Пример. Вычислить

Определение 3. Если определитель состоит из n-строк и n-столбцов, то он называется определителем n-го порядка.
Свойства определителей:
Определитель не меняется при транспонировании (т.е. если в нем строки и столбцы поменять местами с сохранением порядка следования).
Если в определителе поменять местами какие-либо две строки или два столбца, то определитель изменит только знак.
Общий множитель какой-либо строки (столбца) можно выносить за знак определителя.
Если все элементы какой-либо строки (столбца) определителя равны нулю, то определитель равен нулю.
Определитель равен нулю, если элементы каких-либо двух строк равны или пропорциональны.
Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Пример.
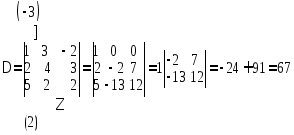
Определение 4. Определитель, полученный из данного путем вычеркивания столбца и строки, называется минором соответствующего элемента. Мij элемента aij .
Определение 5. Алгебраическим дополнением элемента аij , называется выражение

§3. Действия над матрицами
Линейные операции
1)При сложении матриц складываются их одноименные элементы.

При вычитании матриц вычитаются их одноименные элементы.
При умножении матрицы на число каждый элемент матрицы умножается на это число:
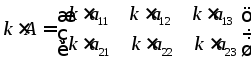
3.2.Умножение матриц.
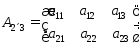

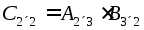
Произведение
матрицы А
на матрицу В
есть новая матрица
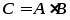 ,
элементы которой равны сумме произведений
элементовi-той
строки матрицы А
на соответствующие элементы j-го
столбца матрицы В.
Произведение матрицы А
на матрицу В
можно находить только в том случае, если
число столбцов матрицы А
равно числу строк матрицы В.
В
противном случае, произведение невозможно.
,
элементы которой равны сумме произведений
элементовi-той
строки матрицы А
на соответствующие элементы j-го
столбца матрицы В.
Произведение матрицы А
на матрицу В
можно находить только в том случае, если
число столбцов матрицы А
равно числу строк матрицы В.
В
противном случае, произведение невозможно.

Замечание:
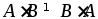 (не подчиняется
свойству коммутативности)
(не подчиняется
свойству коммутативности)
§4. Обратная матрица
Обратная матрица существует только для квадратной матрицы, причем матрица должна быть невырожденной.
Определение 1. Матрица А называется невырожденной, если определитель этой матрицы не равен нулю
Определение 2. А-1 называется обратной матрицей для данной невырожденной квадратной матрицы А, если при умножении этой матрицы на данную как справа, так слева получается единичная матрица.
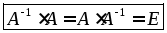
Алгоритм вычисления обратной матрицы
1 способ (с помощью алгебраических дополнений)
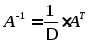
Вычисляем определитель данной матрицы
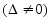 .
.Находим алгебраические дополнения элементов определителя.
Составляем матрицу из этих алгебраических дополнений.
Транспонируем полученную матрицу.
Делим транспонированную матрицу на величину определителя ∆.
Делаем проверку:
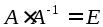
Пример
1:
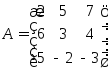
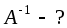
Следовательно, матрица невырожденная и имеет обратную.
Найдем все алгебраические дополнения элементов матрицы:
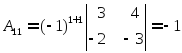
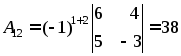

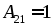
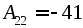

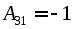

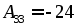
Составим матрицу из алгебраических дополнений:
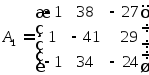
Транспонируем полученную матрицу:
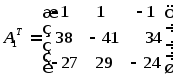
Разделим матрицу
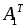 на величину определителя:
на величину определителя:

Проверка:
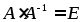
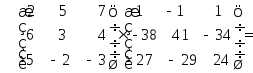

Аналогично
проверяем
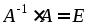 .
Следовательно,
.
Следовательно,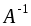 - обратная матрица.
- обратная матрица.

