Курс лекций по высшей математике. 2 часть

	Решение. В момент t заряд конденсатора q и сила тока i	dq	. К
		dt

этому же моменту t в цепи действует электродвижущая сила V, равная

разности между напряжением цепи E и напряжением конденсатора

q

,

c

то есть V

E

q

.

c

По закону Ома сила тока i

V

, или, иначе,

dq

V

E

q с

, от-

R

dt

R

R

куда

dq

E

q

.

Мы получили линейное относительно q уравнение

dt

R

cR

процесса

dq

q

E

(7)

dt

cR

R

Интегрируем это уравнение, полагая q

uv, q

u v uv

и подстав-

ляя

q

и

q

в

уравнение

(7).

Имеем

u v

uv

uv

E

,

cR

R

v u

u

uv

E

, u

u

0

. Тогда

du

u

,

du

dt

, ln u

t

,

cR

R

cR

dt

cR

u

cR

cR

t

t

E

E

t

u

e

cR . Затем получаем e cR v

и

v

e

cR

. Разделим пере-

R

R

E

t

E

t

E

t

t

менные v

и

t:

dv

e cR dt .

Тогда

v

ecR dt

cR

ecR d

R

R

R

cR

t

cEe cR

C

,

где

C

1

–произвольная

постоянная.

Далее

находим

1

t

t

t

q uv, q

e

cR

cEe cR

C

, q

cE

C e cR .

1

1

В момент t

0

согласно условию задачи q

0 ,

так как заряд кон-

денсатора отсутствовал. Тогда при

t

0

и

q

0 имеем

0

cE

C1 и

C1

cE .

Таким образом, закон рассматриваемого процесса описывается ра-

t

венством:

q

cE 1

e cR .

63

§2. Дифференциальные уравнения второго порядка

1. Основные понятия

Дифференциальное уравнение второго порядка можно записать в виде F x, y, y , y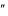 0 . Мы будем рассматривать уравнения второго по-

рядка, которые можно разрешить относительно производной второго порядка, то есть записать в виде

y	f x, y, y .
Для этих уравнений имеет место теорема существования и единст-
венности решения.
Теорема. Если в уравнении		y f x, y, y	функция f x, y, y	и ее
частные производные по аргументам y и y			непрерывны в некоторой
области,	содержащей x0, y0, y0	, то существует и притом единствен-
ное решение y y x уравнения, удовлетворяющее условиям y x0				y0
и y x0	y0 .

Эти условия называются начальными условиями. Геометрический смысл этих условий состоит в том, что через заданную точку плоскости

x0 , y0 с заданным тангенсом угла наклона касательной y0 проходит единственная интегральная кривая. Ясно, что если мы будем задавать различные значения y0, то при постоянных x0 и y0 мы получим бес-

численное множество интегральных кривых с различными углами наклона касательных и проходящих через заданную точку.

Общим решением дифференциального уравнения второго порядка называется функция y 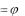x,C1,C2 , зависящая от двух произвольных

постоянных, которая при любых значениях C1 и C2 является решением дифференциального уравнения.

Уравнение Ф x, y,C1,C2 0 , определяющее общее решение, называется общим интегралом дифференциального уравнения.

Если в общее решение подставить конкретные значения С1 и С2 ,

то получится частное решение дифференциального уравнения. График частного решения называют интегральной кривой данного дифференциального уравнения.

Рассмотрим методы решения некоторых уравнений второго поряд-

ка.

64

2. Уравнения, допускающие понижение порядка

а) Рассмотрим простейшее уравнение второго порядка y f x .

Общее решение такого уравнения получается путем двукратного интегрирования:

	y	f x dx C1,
	y	dx f x dx C1x C2 ,
	где	C1 и C2 –произвольные постоянные, а неопределенные инте-
	гралы трактуются как первообразные соответствующих функций.
	Пример 7. Решить уравнение y		x	sin x .
					x2
	Решение. Интегрируя первый		раз,	получаем y		cos x C1 .
					2

Общее решение данного уравнения получаем, интегрируя второй раз:

y

x3

sin x

C1x

C2 .

6

б)

Рассмотрим уравнение y

f x, y

,

явно не содержащее иско-

мую функцию y. Положим y

p .

Тогда

y

p

и уравнение примет

вид

p

f x, p .

Решаем теперь это уравнение первого порядка относительно p, а

затем заменяем p на

y

и решаем последнее уравнение относительно

неизвестной функции y.

Пример 8. Решить уравнение xy

y

0 .

Решение.

Положим

y

p, y

p

и подставим

y

и y

в данное

уравнение.

Получим

xp

p

0, x

dp

p .

Разделим переменные. То-

dx

гда

dp

dx

. Интегрируя, получим ln

p

ln

x

ln

C1

,

ln

p

ln

C1

и

p

x

x

p

C1

. Заменим

теперь p

на

y .

Имеем

dy

C1

, dy

C

dx

и

x

dx

x

1

x

y

C1 ln

x

C2 .

в)

Пусть

y

f

y, y

. Это уравнение явно не содержит перемен-

ную x. Подстановкой

y

p y , y

p

dp

dp

dy

p

p это уравне-

dx

dy

dx

ние приводят к уравнению первого порядка:

p p

f

y, p .

65

Далее получившееся уравнение первого порядка решают относительно вспомогательной функции p, а затем, заменяя p на y, получают

уравнение первого порядка относительно функции y, из которого ее и находят.

Пример 9. Решить уравнение y tgy	2 y 2 .
Решение. Положим y p, y p	p , подставим в уравнение эти

выражения производных и получим дифференциальное уравнение первого порядка относительно вспомогательной функции p:

p

p tgy

2 p2 .

Отсюда

p

p

tgy

2 p2

0, p p tgy

2 p

0 .

Это

уравнение имеет решение p

0 или

y

0 , а

y C , а так же решения,

удовлетворяющие уравнению

p tgy

2 p

0 .

Разделим переменные в этом уравнении:

dp

dp

dy

dp

cos y

tgy

2 p,

2

,

2

dy, ln

p

2ln

sin y

ln

C

. От-

dy

p

tgy

p

sin y

1

куда

p

C sin2 y . Полагая p

y , получим дифференциальное уравне-

1

ние y

C sin2

y .

1

Снова разделим переменные:

dy

C sin2

y,

dy

C dx .

dx

1

sin2 y

1

Интегрируя,

получим:

dy

C1

dx, – ctgy

C1x

C2

или

sin2 y

~

~

ctgy

C1x

C2

. Решение уравнения p=0, то есть y=C, входит в этот об-

~

щий интеграл при

x

0 , так как в таком случае ctgy

C2

и y является

постоянным.

Таким образом, получили общий интеграл дифференциального

уравнения ctgy

C1x

C2 , где C1

и C2 –произвольные постоянные.

3. Линейные однородные уравнения второго порядка. Общие свойства решений

Дифференциальное уравнение второго порядка называется линейным, если оно имеет вид:

y p x y qy	f x ,	(8)
то есть является линейным относительно неизвестной функции y и
ее производных y и y . Коэффициенты	p x и q x	и правая часть
f x этого уравнения непрерывны.

66

Если правая часть уравнения f x 0 , то уравнение называют ли-

нейным неоднородным. Если же f

x

0 , то уравнение имеет вид

y

p x y

qy

0

(9)

и называется линейным однородным.

Пусть y1

y1 x

и

y2

y2 x –какие–либо частные решения урав-

нения (9), то есть не содержат произвольных постоянных.

Теорема 1. Если

y1

и

y2 –два частных решения линейного одно-

родного уравнения второго порядка, то

y1

y2

так же является решени-

ем этого уравнения.

Так как

y1

и

y2 –решения уравнения (9),

то они обращают это

уравнение в тождество, то есть

y1

p x y1

q x y1

0 и y2

p x y2

q x y2

0

(10)

Подставим y1

y2

в уравнение (9). Тогда имеем:

y1

y2

p x y1

y2

q x y1

y2

y1

p x y1

q x y1

y2

p x y2

q x y2

0

0

0

в

силу

(10).

Значит,

y1

y2 –

решение уравнения.

Теорема 2.

Если

y1 –решение линейного однородного уравнения

второго порядка, а C–постоянная, то Cy1

также является решением это-

го уравнения.

Доказательство. Подставим Cy1

в

уравнение (9). Получим:

Cy1

p x Cy1

q x Cy1

C

y1

p x y1

q x y1

С 0 0,

то

есть

Cy1 –решение уравнения.

Следствие.

Если

y1

и

y2 –решения уравнения (9), то C1 y1

C2 y2

так же является его решением в силу теорем (1) и (2).

Определение. Два решения

y1

и

y2

уравнения (9) называются ли-

нейно зависимыми (на отрезке a,b ), если можно подобрать такие чис-

ла	1 и	2 , не равные одновременно нулю, что линейная комбинация
этих	решений тождественно равна нулю на a,b ,		то	есть	если
α1y1	α2 y2	0 .
	Если же таких чисел подобрать нельзя, то решения		y1	и y2	назы-
ваются линейно независимыми (на отрезке a,b ).

67

Очевидно, решения y1 и y2 будут линейно зависимы тогда и толь-

ко тогда, когда их отношение постоянно,

то есть

y1

(или наоборот

y2

y2

).

y1

В самом деле, если

y1 и y2 –линейно зависимы, то

1 y1

2 y2

0 ,

где по меньшей мере одна постоянная

1

или

2

отлична от нуля.

Пусть,

например,

0

. Тогда y

2

y

2

0 ,

y

2

y

2

,

y1

2

.

1

1

1

y2

1

1

1

Обозначая

2

,

получим

y1

, то

есть отношение

y1

–

1

y2

y2

постоянно.

Обратно, если

y1

, то y1

αy2, y1

αy2

0 . Здесь коэффициент

y2

при y1

1 , то есть отличен от нуля, что по определению означает, что

y1 и y2 являются линейно зависимыми.

Замечание. Из определения линейно независимых решений и рассуждений выше можно сделать вывод, что если y1 и y2 –линейно независимы, то их отношение не может быть постоянным.

Например, функции				ek1x и ek2 x	при k			k	2	–линейно независимы,
						1
так как	ek1x		e k1 k2 x	, так как	k k			0 . А вот функции 5x и x–
						2
	ek2 x				1
линейно зависимы, так как их отношение						5x		5 .
						x
Теорема.			Если y1 и	y2 –линейно независимые частные решения

линейного однородного уравнения второго порядка, то их линейная комбинация C1 y1 C2 y2 , где C1 и C2 –произвольные постоянные, явля-

ется общим решением этого уравнения.

Доказательство. В силу теорем 1 и 2 (и следствия к ним) C1 y1 C2 y2 является решением уравнения (9) при любом выборе посто-

янных C1 и C2 .

Если решения y1 и y2 –линейно независимы, то C1 y1 C2 y2 –общее

решение, так как это решение содержит две произвольные постоянные, которые не могут быть сведены к одной.

68

В тоже время, если бы					y1 и	y2 были линейно зависимыми реше-
ниями, то C1 y1			C2 y2 уже не являлось бы общим решением. В этом
случае	y1		,	где		α–константа.	Тогда	y1	y2 ,
	y2
C1 y1 C2 y2 C1			y2	C2 y2	C1	C2 y2 Cy2 , где C C1		C2	явля-

ется постоянной. Cy2 не может быть общим решением дифференци-

ального уравнения второго порядка, так как зависит лишь от одной постоянной.

Итак, общее решение уравнения (9):

	y C1 y1 C2 y2	(11)
где	y1 и y2 –линейно независимые частные решения этого уравне-
ния, а C1	и C2 –произвольные постоянные.

4.Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Пусть линейное				однородное			дифференциальное			уравнение
y py	qy	0 (9) имеет постоянные коэффициенты p и q. Будем ис-
кать частные решения этого уравнения в виде
				y	ekx , где k			const.		(12)
Найдем y		и y	из формулы (12): y					kekx, y	k 2ekx.
Подставим			y, y , y		в		уравнение		(9).	Получим:
k 2ekx	pkekx	qekx	0,	ekx k 2	px	q	0. Но ekx		0 . Поэтому
					k 2	pk	q	0		(13)

Квадратное уравнение (13), из которого определяется число k, называется характеристическим уравнением данного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.

Заметим, что для составления характеристического уравнения достаточно в дифференциальном уравнении производные y и y заме-

нить на k и k 2 , а функцию y рассматривать как производную нулевого

порядка и y заменить на k 0 , то есть на единицу.

Например, характеристическое уравнение дифференциального уравнения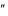 y 9y 6y 0 имеет вид k 2 9k 6 0 .

69

	Решим характеристическое уравнение.
			k1,2	p		p2		q			(14)
				2		4
	При этих значениях k функции ekx будут решениями уравнения (9).
	Возможны три различных случая.
		p2
	Случай I. Если		q 0 , то корни характеристического уравне-
		4
	ния действительны и различны, то есть					k1		k2 . Тогда частными реше-
	ниями уравнения (9) будут функции y					ek1 x		и y		2	ek2 x . Эти функции
				1

линейно независимы и, следовательно, общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами будет:

y C ek1x	C	ek2 x	(15)
1	2
Пример 10. Найти общее решение уравнения y			5y 6y 0 .

Решение. Составим характеристическое уравнение и найдем его корни.

k 2 5k 6 0, k	5			25			6		5			1		.	k	5 1		3, k		5 1	2.
																			2
1,2	2			4			2			4					1	2				2
Тогда общее решение дифференциального уравнения составляем
по формуле (15): y	C e2 x			C		2	e3x .
	1

		p2
	Случай II. Если		q 0	, то в силу формулы (14) характеристи-
		4
	ческое уравнение (13) имеет равные корни				k	k		p	. Такие корни
							2
					1			2

называются кратными. В этом случае одно частное решение дифферен-

p

ekx

x . Другое частное решение,

циального уравнения будет

y

e

2

1

линейно независимое с y1 ,

следует выбрать так, чтобы

y2

const. То-

y1

гда

y2

z x

, что и означает,

что y2

и

y1 –линейно независимы. Най-

y1

дем y2

z x

y1 , определив функцию z x , подставляя

y2 в дифферен-

70

p

x

циальное

уравнение.

y

2

z x e

2 .

Тогда

p

p

p

p

p

p

p

p

z e

x

ze

x

e

x

z , y

e

x

z

y

2

2

2

2

z

2

2

z

2

2

2

2

p

p

p

p

2

p

p2

e

x z

z

e

x z

x z

2

2

pz

z

e

2

pz

z .

2

2

4

Подставляя y2, y2

и

y2

в уравнение

y

py

qy

0 ,

получим

p

p2

p

p

p

x

x

z

qe

x z

e

2

z

pz

z

pe

2

z

2

0 .

Вынося за скобки

4

2

p

x

общий множитель

e 2

и сокращая на него,

что возможно,

так как

p

p2

p2

x

z

e

2

0 ,

получим

далее

z

pz

z

pz

qz

0

или

4

2

p

2

p2

p2

z

z

qz

0 и

z

q

z

0 .

Но

q

0 ,

поэтому имеем

4

4

4

z

0 , откуда

z

a и z

ax

b , где a и b–постоянные. Но так как мы

ищем какое–либо частное решение дифференциального уравнения, то

p

x или

xekx .

можно взять a 1 и b 0 . Тогда

z

x , a

y

2

xe

2

y

2

Таким образом, мы имеем два линейно независимых частных ре-

шения линейного уравнения:

y

ekx

и y

2

xekx . Тогда общее решение

1

этого уравнения будет иметь вид:

y

C ekx

C

2

xekx

или y

ekx

C

xC

2

(16)

1

1

Пример 11. Решить дифференциальное уравнение

y 6y 9y

0 .

Решение. Составим характеристическое уравнение этого диффе-

ренциального уравнения:

k 2

6k

9

0 . Тогда k

3 2

0 и k 3 . Об-

щее решение данного дифференциального уравнения составляем по

формуле (16): y	e3x C			xC	2	.
		1
Случай III. Если		p	2	q		0 , то на основании формулы (14) харак-
		4
теристическое	уравнение					(13)	имеет	комплексные	корни:

71

	p		p2		p		p2			где	p	,
k				q		q		1	i,
1,2	2	4			2		4				2

p2

. Таким образом, k

i,

k

i. Тогда

β

q

, i

1

2

4

1

частные решения линейного однородного уравнения

y

py

qy

0

будут иметь вид:

y

ek1 x

e α βi x ,

y

2

ek2 x

e α

βi x.

1

Тогда общее решение уравнения формально можно записать так:

βi x

e α

βi x

eαx e βix

eαx e

βix

eαx

e βix

ix

y

C

e α

C

2

C

C

2

C

C

2

e

,

1

1

1

где C1 и C2 –некоторые комплексные постоянные, подобранные таким

образом, чтобы общее решение было действительным. Избавимся в последнем выражении от мнимых величин, воспользовавшись формулами Эйлера:

e βix	cos βx	i sin βx,
e βix	cos βx	i sin βx.

Отсюда

y

e

x C cos

x

i sin x

C

cos x

i sin x

1

2

eαx

C

C

2

cos βx

i C

C

2

sin βx

eαx

C cos βx

C

2

sin

x ,

где C

1

1

1

1

и C2 –какие угодно (ввиду произвольности постоянных C1

и

C2 ) дей-

ствительные постоянные. Таким образом, если характеристическое уравнение имеет комплексные корни, то общее решение линейного однородного уравнения находится по формуле:

		y	e x C cos x	C	2	sin	x			(17)
			1
Пример 12. Составить общее решение дифференциального уравне-
ния y	4 y 13y	0 .
Решение. Составим характеристическое уравнение и найдем его
корни.	Имеем k 2	4k 13	0 . Отсюда
				k		2	4 13 2			9
				1,2

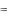2 3i . Тогда согласно формуле (17) получаем общее решение данно-

го дифференциального уравнения	y e	2 x C cos 3x	C	2	sin 3x .
		1

В заключение этого пункта составим таблицу, использование которой облегчает студенту отыскание общего решения уравнения

y py qy 0 .

72