Дискретная математика / Алгебра - логики

МИНИМИЗАЦИЯ ФУНКЦИЙ АЛГЕБРЫ ЛОГИКИ

Основные положения

Функцией алгебры логики называется функция дающая однозначное отображение Х в Y. Сокращенно функция алгебры логики обознается ФАЛ. Наборы <х1, х2, х3,…,хn> могут рассматриваться как наборы значений аргументов ФАЛ.

Рассмотрим функции, которые играют большую роль в построении теории функций алгебры логики и ее приложениях. Эти функции мы будем назы­вать в дальнейшем элементарными.

Имеем только две функции совпадающие с константами 0 и 1:

f1 = 0

f2 = 1

Также еще имеется две функции зависящие от аргумента х1:

f3 = x

f4 =

Эти четыре функции являются элементарными, где f4 называется функцией отрицания.

Все остальные функции зависят от двух аргументов х1 и х2 и представлены в следующей таблице:

х1	х2	f5	f6	f7	f8	f9	f10	f11
0	0	0	0	1	1	1	1	0
0	1	1	0	0	1	0	1	1
1	0	1	0	0	0	0	1	1
1	1	1	1	1	1	0	0	0

Функция f5 - определяемая этой таблицей, носит на­звание дизъюнкции или логического сложения (x1 v х2).

Функция f6 – носит название конъюнкции или логического умножения (х1 & х2).

Функция f7 - носит название функции эквивалент­ности или функции равнозначности (х1~ х2).

Функция f8 - носит название импликации или логического следования (х1→х2).

Функция f9 - носит название функции Вебба, штрих Пирса (х1 ↓ х2).

Функция f10 – носит название функции Шеффера (х1 / х2).

Функция f11 – обычно называется функцией сложения по модулю 2 (х1 х2).

Любая функция алгебры логики может быть записана в виде ДСНФ или КСНФ. такая запись в ряде случаев является неэкономной. Проблема простейшего представления функций сводится к проблеме выбора базиса и проблеме наибо­лее экономного представления функций в этом базисе. В настоящее время существенные результаты в решении задачи минимизации получены лишь для базиса, со­стоящего из отрицания, конъюнкции и дизъюнкции.

Для уточнения постановки задачи о минимиза­ции дадим ряд определений:

1. Конъюнкция назы­вается элементарной, если в этой конъюнкции каждая переменная встречается не более одного раза.

2. Рангом элементарной конъюнк­ции называется число букв, образующих эту конъюнк­цию.

3. Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).

4. Дизъюнктивная нормальная форма для функции f(x1, x2, ..., х_n), состоящая из эле­ментарных конъюнкций ранга n, называется дизъюнктив­ной совершенной нормальной формой.

5. Длиной ДНФ назовем число элементарных конъюнкций, образующих эту ДНФ. Длину ДНФ будем обозначать буквой L.

6. Дизъюнктивная нормальная форма, имеющая наименьшую длину по сравнению со всеми другими ДНФ, эквивалентными данной функции, называется кратчайшей ДНФ (КДНФ).

7. Дизъюнктивная нормальная форма, содержащая наименьшее число букв x_i по сравнению со всеми другими ДНФ, эквивалентными данной функции, называется минимальной ДНФ (МДНФ).

Для минимизации функций алгебры логики от любого числа аргументов используются следующие методы:

1. Метод неопределенных коэффициентов.

Представим функцию f(x1, х2, х3) в виде следующей ДНФ:

Здесь представлены все возможные конъюнктивные члены, которые могут входить в дизъюнктивную форму представления f(x1, x2, x3). Коэффициенты К с различ­ными индексами являются неопределенными и подби­раются так, чтобы получающаяся после этого дизъюнк­тивная форма была минимальной. Если теперь задавать всевозможные наборы значений аргументов <х1, х2, х3> и приравнивать полученное после этого выражение (от­брасывая нулевые конъюнкции) значению функции на выбранных наборах, то получим систему 2³ уравнений для определения коэффициентов К:

(1)

Пусть таблично задана некоторая функция f(x1, х2, х3). Задание некоторой конкретной функции опреде­ляет значения правых частей системы (2-11). Если на­бор <х1, х2, х3> таков, что функция на этом наборе равна нулю, то в правой части соответствующего урав­нения будет стоять нуль. Для удовлетворения этого уравнения необходимо приравнять нулю все коэффи­циенты К, входящие в левую часть рассматриваемого уравнения. (Это вытекает из того, что дизъюнкция рав­на нулю только тогда, когда все члены, входящие в нее, равны нулю).

Рассмотрев все наборы, на которых данная функция обращается в нуль, получим все нулевые коэффициен­ты К. В уравнениях, в которых справа стоят единицы, вычеркнем слева все нулевые коэффициенты. Из остав­шихся коэффициентов приравняем единице коэффициент, определяющий конъюнкцию наименьшего возможного ранга, а остальные коэффициенты в левой части дан­ного уравнения примем равными нулю (это можно сделать, так как дизъюнкция обращается в единицу, если хотя бы один член ее равен единице). Единичные коэф­фициенты К_i определят из (1) соответствующую ДНФ.

Описанный метод эффективен лишь для минимиза­ции функций, число аргументов в которых не больше 5—6. Это связано с тем, что число уравнений равно 2ⁿ.

Более эффективным является выписывание не всех возможных конъюнкций для функции n переменных, а только тех, которые могут присутствовать в ДНФ, эквивалентной минимизируемой функции. Этот прием позволяет уменьшить таблицу и перебор, который мы проводим с целью нахождения МДНФ.

2. Метод Квайна – Мак-Класки.

При минимизации по методу Квайна предполагается, что минимизируемая функция задана в ДСНФ. Для простоты будем называть элементарные конъюнкции ранга n, входящие в ДСНФ минимизируемой функции, мииитермами ранга n. Метод Квайна состоит из после­довательного выполнения следующих этапов:

1). Нахождение первичных импликант. Все минитермы данной функции сравнивают между собой попарно. Если минитермы mi и mj таковы, что они имеют вид и , то выписывается конъюнкция а, являющаяся минитермом (n—1) -го ранга. Минитермы n-го ранга, для которых произошло склеивание, отмечаются. После построения всех минитермов

(n -1)-го ранга вновь срав­нивают их попарно, выписывают минитермы (n - 2)-го ранга и отмечают склеивающиеся минитермы (n -1)-го ранга и т. д. Этап заканчивается, когда вновь получен­ные минитермы l-го ранга уже не склеиваются между собой. Все не отмеченные мннитермы называются пер­вичными или простыми импликантами.

Пример 1.

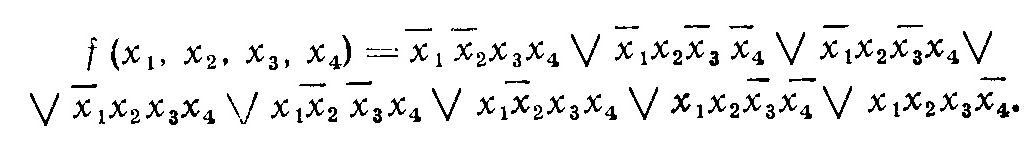
Минитермы 4-го ранга:

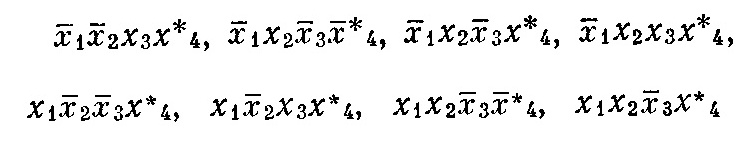
Образуем минитермы 3-го ранга:

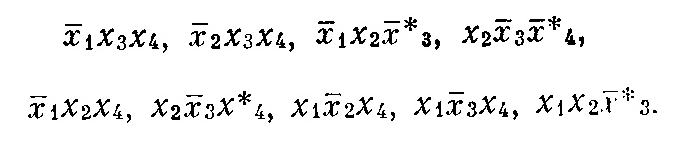
Теперь находим минитермы 2-го ранга:

Так как дальнейшее склеивание невозможно, то этап получения простых импликант закончен. Простыми импликантами являются следующие мннитермы:

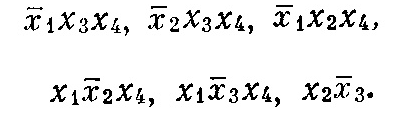
2). Расстановка меток. Для данной функции:

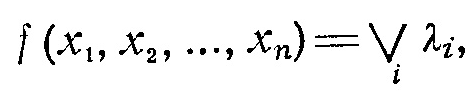
(2)

где λi — простые импликанты, полученные нами на пер­вом этапе. Соотношение (2) определяет СДНФ для данной функции. Для нахождения минимального покры­тия интервалами максимального ранга необходимо те­перь произвести выбрасывание некоторого количества первичных импликант. На этапе расстановки меток со­ставляется таблица, число строк которой равно числу полученных первичных импликант минимизируемой функции. Число столбцов совпадает с числом минитермов ДСНФ. Если в некоторый минитерм ДСНф входит какой-либо из первичных импликант, то на пересечении соответствующего столбца и строки ставится метка.

Составим таблицу с метками для рассматриваемой функции, в которой будет шесть строк и восемь столбцов:

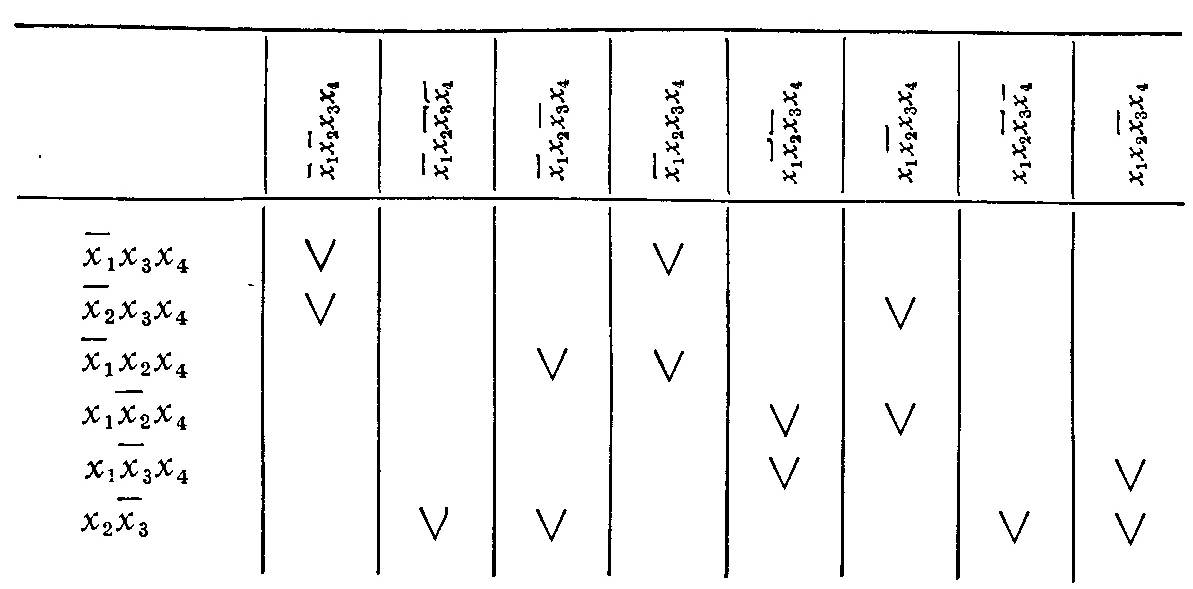
3). Нахождение существенных импликант. Если в ка­ком-либо из столбцов составленной таблицы имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной импликантой. Существенная импликанта не может быть исключена из правой части (2), так как без нее не будет получено покрытие всего множества Т₁ данной функции. Поэтому из таблицы меток исключаются строки, соответствующие существенным импликантам, и столбцы минитермов, покрываемых этими существенны­ми импликантами. Для нашей функции сущест­венной импликантой является . Она покрывает

минитермы.При переходе к следующему этапу эти минитермы могут быть вы­черкнуты.

4). Вычеркивание лишних столбцов. Исследуется таб­лица, полученная после третьего этапа. Если в ней есть два столбца, в которых имеются метки в одинаковых строках, то один из них вычеркивается. Это можно сделать в силу того, что покрытие оставшегося столб­ца будет осуществлять покрытие выброшенного минитерма.

После вычеркиваний сущест­венной импликанты и минитермов, которые она покрывает, табли­ца меток принимает вид:

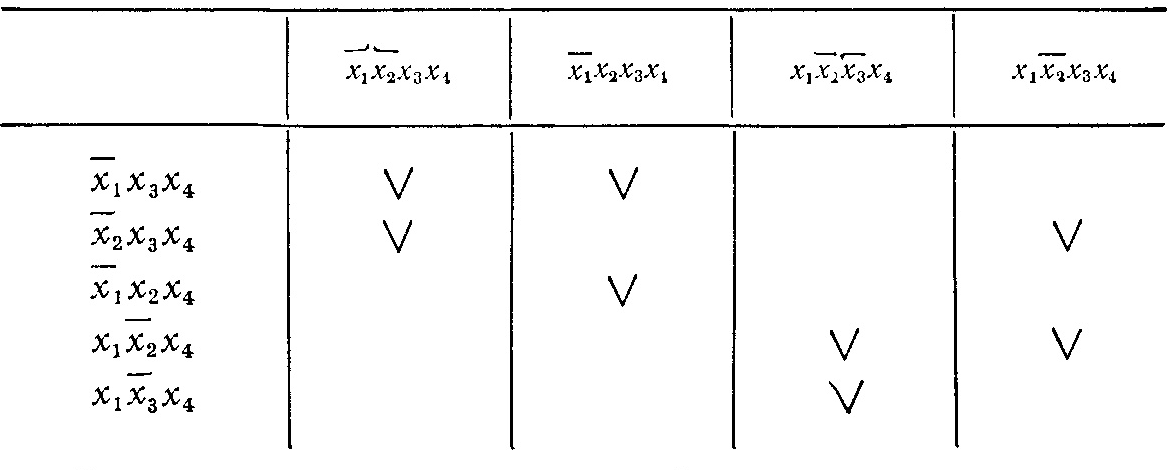
В данном случае одинаковых столбцов нет.

5). Вычеркивание лишних первичных импликант. Если после выбрасывания некоторых столбцов на четвертом этапе в таблице появляются строки, в которых нет ни одной метки, то первичные импликанты, соответствующие этим строкам, исключаются из дальнейших рассмот­рений, так как они не покрывают оставшиеся в рассмот­рении минитермы.

6). Выбор минимального покрытия максимальными интервалами. Исследуется полученная таблица. Выбирается такая совокупность первичных импликант, кото­рая включает метки во всех столбцах (по крайней мере по одной метке в каждом столбце). При нескольких возможных вариантах такого выбора отдается предпочте­ние варианту покрытия с минимальным суммарным чис­лом букв в простых импликантах, образующих покры­тие.

Для рассматриваемой функции выбираем покрытие из импликант и , так как они сов­местно покрывают все оставшиеся после четвертого этапа миннтер-мы. Минимальная ДНФ для этой функции имеет вид:

В методе Квайна есть одно существенное неудобст­во. Оно связано с необходимостью полного попарного сравнения на этапе нахождения простых импликант. С ростом числа минитермов, определяющих ДСНФ дан­ной функции, растет число этих сравнений. Этот рост характеризуется факториальной функцией. Поэтому при достаточно большом числе минитермов применение ме­тода Квайна становится затруднительным. В 1956г. Мак-Класки предложил модернизацию первого этапа метода Квайна, дающую существенное уменьшение чи­сла сравнений минитермов.

Идея Мак-Класки заключается в следующем. Если записать минитермы в виде их двоичных номеров, то все номера можно разбить по числу единиц в этих номе­рах на непересекающиеся группы. При этом в i-ю груп­пу войдут все номера, имеющие в своей двоичной записи ровно i единиц. Попарное сравнение можно производить только между соседними по номеру группами, так как только эти группы отличаются для входящих в них минитермов в одном разряде. При образовании мини­термов с рангом выше нулевого в разряды, соответствую­щие исключенным переменным, пишется знак тире. Такая модификация, кроме того, на практике чрезвычайно удобна, так как позволяет избежать выписывания гро­моздких минитермов и импликант, заменяя эту про­цедуру выписыванием их двоичных номеров.

Пример. Функция задана в ДСНФ минитермами с номерами 0, 1, 2, 3, 4, 6, 7, 8, 9, 11, 15. Запишем эти минитермы по группам в двоичном коде.

Нулевая группа: 0000*.

Первая группа: 0001*, 0010*, 0100* 1000*.

Вторая группа: 0011*, 0110*, 1001*.

Третья группа: 0111*, 1011*.

Четвертая группа: 1111*.

Сравнивая соседние группы, получаем по группам минитермы 3-го ранга:

Нулевая группа: 000 -*, 00 - 0*, 0 - 00*, - 000*.

Первая группа: 00 - 1*, - 001*, 001 - *, 0 - 10*, 01 - 0*, 100 - *.

Вторая группа: 0 - 11*, - 011*, 011 - *, 10 - 1*.

Третья группа: - 111*, 1 - 11*.

Теперь находим минитермы 2-го ранга:

Нулевая группа: 00 - - , - 00 -, 0 - - 0,

Первая группа: - 0 - 1, 0 – 1 -.

Вторая группа: - - 11.

Составляем таблицу меток:

Дальнейшая минимизация по методу Мак-Класки совпадает с минимизацией по методу Квайна. Для рассматриваемой функции минимальная ДНФ имеет следующий вид: