Изучение основного закона динамики вращательного движения на маятнике Обербека

Цель работы: изучить зависимость углового ускорения абсолютно твердого тела (а.т.т.) от момента вращающей силы и момента инерции.

Приборы и принадлежности:

1. Маятник Обербека;

2. Набор перегрузков;

3. Секундомер;

4. Масштабная линейка;

5. Штангенциркуль.

1. Краткая теория

1. Основной закон динамики вращательного движения (а.Т.Т.)

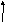
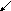
Рассмотрим тело произвольной формы, которое может вращаться вокруг неподвижной произвольной оси Z (рис.1), причем ось Z может проходить как через тело, так и вне его. Подействуем на тело силой F, приложенной к точке, находящейся на расстоянии r от оси вращения. Так как тело абсолютно твердое, то работа силы F равна работе, затраченной на поворот всего тела. Разложим вектор внешней силы на три вектора:

– составляющая силы параллельная оси вращения – она может переместить тело вверх–вниз;

– составляющая силы перпендикулярная оси вращения – может переместить тело вправо–влево и – тангенциальная составляющая силы, которая может изменить скорость вращения тела. При повороте тела на бесконечно малый угол точка приложения силы проходит по дуге .

Работа, совершенная этой (вращающей) силой:

(1)

Произведение вращающей силы на расстояние от оси до точки приложения силы определяет момент вращающей силы () относительно произвольной оси Z по формуле:

.

Таким образом, работа при вращении тела равна произведению момента вращающей силы на угол поворота

(2)

Работа, при повороте тела на угол , идет на увеличение его кинетической энергии .

Но изменение кинетической энергии вращающегося тела

(3)

где – момент инерции тела относительно произвольной оси.

Учитывая, что угловая скорость , а ускорение и приравнивая выражения (2) и (3) получим ,

(4)

Уравнение (4) выражает основной закон динамики вращательного движения а.т.т. относительно неподвижной оси. Если ось Z проходит через центр масс (главная ось инерции), то формулу (4) можно переписать в векторном виде:

, где – главный момент инерции тела.

Момент импульса тела (L_z) относительно произвольной оси .

Продифференцируем последнее выражение по времени

.

Правые части, полученной формулы и формулы (4) равны, следовательно:

(5)

Формула (5) это второй вид записи основного уравнения динамики вращающегося а.т.т., которое также называют – уравнением моментов.

2. Теория метода и описание установки

Экспериментально исследовать выполнимость основного закона динамики вращательного движения можно на маятнике Обербека (рис.2).

рис.2 Маятник Обербека

Маятник состоит из двух шкивов радиусом r₁ и r₂, четырех тонких стержней, укрепленных на втулке под прямым углом друг другу и четырех одинаковых цилиндров массой m_ц, радиусом r_ц и высотой _ц. Втулка и шкивы насажены на общую ось. Ось закреплена в игольчатых подшипниках так, что вся система может свободно вращаться вокруг горизонтальной оси. Цилиндры можно перемещать вдоль стержней и закреплять на определенном расстоянии от оси вращения; они закрепляются симметрично, так, чтобы центр тяжести всей системы совпадал с осью вращения. Перемещение цилиндров приводит к изменению момента инерции прибора.

Система приводится во вращательное движение силой тяжести () груза, прикрепленного к концу шнура, навитого на один из шкивов. Груз массой m, удерживаемый на высоте h над какой – либо поверхностью (например, пола) обладает потенциальной энергией mgh.

Если представить возможность грузу падать, то он будет двигаться с ускорением . При этом шкив со стержнями и расположенными на нем цилиндрами будет вращаться с угловым ускорением . Измеряя время прохождения грузом высоты h можно определить линейное и угловое ускорения и скорость груза в момент касания пола.

(6)

При падении груза его потенциальная энергия переходит в кинетическую энергию поступательного движения груза и кинетическую энергию вращательного движения системы

(7)

Решая уравнение (7) находим момент инерции системы

(8)

При проведении экспериментов необходимо учитывать, что mg – это сила тяжести перегрузка, вызывающего ускоренное движение.

Момент вращающей силы:

(9)

В реальных опытах существует сила трения и момент сил трения.

(10)

может оказаться достаточно большим и существенно исказить результаты опыта. В маятнике Обербека момент сил трения снижается благодаря креплению оси маятника в игольчатых подшипниках, однако влияние трения вполне ощутимо и его необходимо учитывать при обработке результатов опыта.

В каждом опыте достаточно просто оценить силу трения () по минимальной массе платформы и дополнительных грузиках при которых () начинается движение.

Момент вращающей силы (9) оценивается по дополнительным (по отношению к ) перегрузкам.