
- •Змістовий модуль 8.
- •8.1.2. Властивості невизначеного інтеграла
- •8.1.3. Таблиця основних невизначених інтегралів
- •8.2. Основні методи інтегрування
- •8.2.1. Метод безпосереднього інтегрування
- •8.2.3. Метод інтегрування частинами
- •8.3. Інтегрування раціональних функцій
- •8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру)
- •Дробово-раціональна функція
- •8.3.2. Інтегрування найпростіших раціональних дробів
- •8.3.3. Інтегрування раціональних дробів
- •8.4. Інтегрування тригонометричних функцій
- •8.4.1. Універсальна тригонометрична підстановка
- •8.4.2. Інтеграли виду
- •8.4.3. Використання тригонометричних перетворень
- •8.5. Інтегрування ірраціональних функцій
- •8.5.1. Квадратичні ірраціональності
- •8.5.2. Дробово-лінійна підстановка
- •8.5.3. Тригонометрична підстановка
- •8.5.4. Інтеграли виду
- •8.5.5. Інтегрування диференціального бінома
- •8.6. Інтеграли, що «беруться» і «не беруться»
Змістовий модуль 8.
НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
Тема 8.1. Невизначений інтеграл.
8.1.1. Означення невизначеного інтеграла.
8.1.2. Властивості невизначеного інтеграла.
8.1.3. Таблиця основних невизначених інтегралів.
Тема 8.2. Основні методи інтегрування.
8.2.1. Метод безпосереднього інтегрування.
8.2.2. Метод інтегрування підстановкою (заміна змінної).
8.2.3. Метод інтегрування частинами.
Тема 8.3. Інтегрування раціональних функцій.
8.3.1. Поняття про раціональні функції.
8.3.2. Інтегрування найпростіших раціональних дробів.
8.3.3. Інтегрування раціональних дробів.
Тема 8.4. Інтегрування тригонометричних функцій.
8.4.1. Універсальна тригонометрична підстановка.
8.4.2.
Інтеграли виду
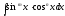 .
.
8.4.3. Використання тригонометричних перетворень.
Тема 8.5. Інтегрування ірраціональних функцій.
8.5.1. Квадратичні ірраціональності.
8.5.2. Дробово - лінійна підстановка.
8.5.3. Тригонометрична підстановка.
8.5.4.
Інтеграли виду
 .
.
8.5.5. Інтегрування диференціального бінома.
Тема 8.6. Інтеграли, що «беруться» і «не беруться».
8.1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
8.1.1. Означення невизначеного інтеграла
В
диференціальному численні розв'язується
задача: по даній функції
 знайти її похідну (або диференціал).
Інтегральне числення вирішує зворотну
задачу: знайти функцію
знайти її похідну (або диференціал).
Інтегральне числення вирішує зворотну
задачу: знайти функцію ,
знаючи її похідну
,
знаючи її похідну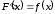 (або диференціал). Шукану функцію
(або диференціал). Шукану функцію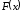 називаютьпервісною
функції
називаютьпервісною
функції
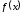 .
.
Функція
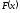 називаєтьсяпервісною
функції
називаєтьсяпервісною
функції
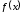 на інтервалі
на інтервалі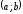 ,
якщо для будь-кого
,
якщо для будь-кого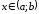 виконується рівність
виконується рівність
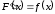 (або
(або
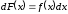 ) .
) .
Наприклад,
первісною функції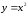 ,
,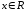 ,
є функція
,
є функція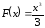 ,
оскільки
,
оскільки
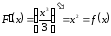 .
.
Очевидно, що первісними будуть також будь-які функції
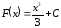 ,
,
де
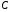 – стала, оскільки
– стала, оскільки
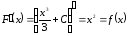
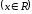 .
.
Теорема
8.1.1.
Якщо
функція
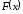 є первісною функції
є первісною функції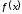 на
на ,
то множина всіх первісних для
,
то множина всіх первісних для задається формулою
задається формулою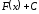 ,
де
,
де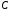 – стала.
– стала.
Функція
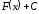 є первісною
є первісною .
Дійсно
.
Дійсно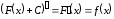 .
.
Нехай
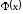 - деяка інша, відмінна від
- деяка інша, відмінна від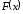 ,
первісна функції
,
первісна функції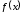 ,
тобто
,
тобто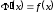 .
Тоді для будь-якого
.
Тоді для будь-якого маємо
маємо
 .
.
А це означає (див. наслідок 25.1), що
рис. 166.
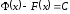 ,
,
де
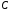 – стале число. Отже,
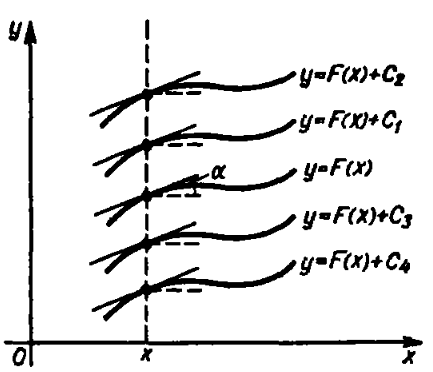
– стале число. Отже,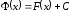 .
.
Множина
всіх первісних функцій
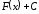 для
для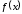 називаєтьсяневизначеним
інтегралом
від функції
називаєтьсяневизначеним
інтегралом
від функції
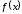 і позначається символом
і позначається символом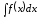 .
.
Таким чином, за означенням
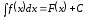 .
.
Тут
 називається підінтегральною функцією,
називається підінтегральною функцією,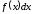 –
підінтегральним
виразом,
–
підінтегральним
виразом,
 – змінною інтеграції,
– змінною інтеграції,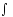 – знак невизначеного інтеграла.
– знак невизначеного інтеграла.
Операція знаходження невизначеного інтеграла від функції називається інтегруванням цієї функції.
Геометрично
невизначений інтеграл є сімейством
«паралельних кривих»
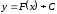 (кожному числовому значенню
(кожному числовому значенню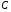 відповідає
певна крива сімейства) (див. рис. 166).
Графік кожної первісної (кривої)
називається інтегральною
кривою.
відповідає
певна крива сімейства) (див. рис. 166).
Графік кожної первісної (кривої)
називається інтегральною
кривою.
Чи для всякої функції існує невизначений інтеграл?
Має
місце теорема, що стверджує, що «будь-яка
неперервна на
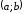 функція
має на цьому проміжку первісну», а отже,
і невизначений інтеграл.
функція
має на цьому проміжку первісну», а отже,
і невизначений інтеграл.
8.1.2. Властивості невизначеного інтеграла
Визначимо ряд властивостей невизначеного інтеграла, виходячи з його визначення.
1. Диференціал від невизначеного інтеграла, рівний підінтегральному виразу, а похідна невизначеного інтеграла рівна підінтегральній функції:
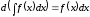 ,
,
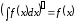 .
.
Дійсно,

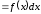 і
і
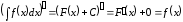 .
.
Завдяки цій властивості правильність інтеграції перевіряється диференціюванням. Наприклад, рівність

правильна,
оскільки
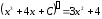 .
.
2. Невизначений інтеграл від диференціала деякої функції рівний сумі цієї функції і довільної сталої:
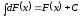 .
.
Дійсно,
 .
.
3. Сталий множник можна виносити за знак інтеграла:
 ,
,
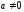 – стала.
– стала.
Дійсно,
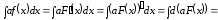
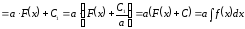
(Поклали
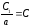 ).
).
4. Невизначений інтеграл від алгебраїчної суми скінченного числа неперервних функцій рівний алгебраїчній сумі інтегралів від складових функцій:
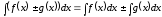 .
.
Нехай
 і
і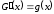 .
Тоді
.
Тоді
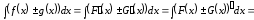
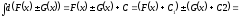
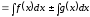 ,
де
,
де
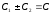 .
.
5.
(Інваріантність формули інтеграції).
Якщо
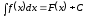 ,
то й
,
то й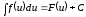 ,
де
,
де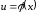 – довільна функція, що має неперервну
похідну.
– довільна функція, що має неперервну
похідну.
Нехай
 –
незалежна змінна,
–
незалежна змінна,
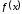 –
неперервна функція і
–
неперервна функція і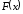 – її первісна. Тоді
– її первісна. Тоді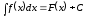 .
Покладемо тепер
.
Покладемо тепер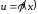 ,
де
,
де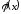 – функція, що неперервно диференціюється.
Розглянемо складну функцію
– функція, що неперервно диференціюється.
Розглянемо складну функцію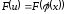 .
Через інваріантність форми першого
диференціала функції маємо
.
Через інваріантність форми першого
диференціала функції маємо
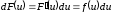 .
.
Звідси
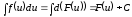 .
.
Таким чином, формула для невизначеного інтеграла залишається справедливою незалежно від того, чи є змінна інтеграції незалежною змінною або будь-якою функцією від неї, що має неперервну похідну.
Так,
з формули
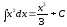 шляхом заміни
шляхом заміни на
на

 одержуємо
одержуємо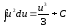 .
Зокрема
.
Зокрема
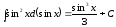 ,
,
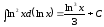 ,
,
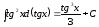 .
.
Приклад
1.
Знайти
інтеграл
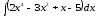 .
.
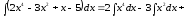
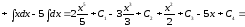
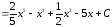 ,
де
,
де
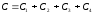 .
.
Приклад
2.
Знайти інтеграл
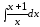 .
.
 .
.
