матан 3 курс 2013 / лекции / Невизначений інтеграл / лекция № 2

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 2

з теми: «Первісна та невизначений інтеграл. Основні властивості інтеграла. Методи інтегрування.»

Модуль КЗН-02. ПР.О.03.07 Невизначений інтеграл.

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІI

Викладач: Велікодна Ольга Володимирівна.

Тема: Первісна та невизначений інтеграл. Основні властивості інтеграла. Методи інтегрування.

Мета:

• Дидактична: навчитися обчислювати первісну, володіти методами інтегрування, знаходити первісну раціональних функцій, трансцендентних та ірраціональних функцій.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики пошукової технології.

Тип: лекція

Вид: лекція – дослідження.

Методи та форми проведення заняття: словесні, наглядні, проблемно – пошукові.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

4. Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: таблиця похідних, таблиця інтегралів основних елементарних функцій.

3. Вивчення нового матеріалу:

• Тема лекції: Первісна та невизначений інтеграл. Основні властивості інтеграла. Методи інтегрування.

• Мотивація вивчення матеріалу: основний математичний апарат – невизначений інтеграл - дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 2.

Тема: Первісна та невизначений інтеграл. Основні властивості інтеграла. Методи інтегрування.

План лекції № 2.

1. Основні властивості невизначеного інтеграла.

2. Формула заміни змінного.

3. Формула інтегрування за частинами.

1. Нехай всі функції, що розглядаються визначені на фіксованому проміжку Δ. Розглянемо властивості інтеграла, що послідкують з його визначення.

   1. Якщо функція F диференційована на проміжку Δ, то ∫dF(х) = F(х) + С, тобто ∫F′(х)dх = F(х) + С.

   2. Нехай функція ƒ має первісну на проміжку Δ; тоді для всіх х Δ має місце рівність d(∫ƒ(х)dх) = ƒ(х)dх.

   3. Якщо функції ƒ та ƒ мають первісні на проміжку Δ, то й функція ƒ + ƒ має первісну на цьому проміжку, причому ∫(ƒ(х) + ƒ(х))dх = ∫ƒ(х)dх + ∫ƒ(х)dх.

   4. Якщо функція ƒ має первісну на проміжку Δ та k – стала, то функція kƒ також має на Δ первісну та при k ≠ 0 вірна рівність ∫kƒ(х)dх = k∫ƒ(х)dх.

   5. Наслідки. Якщо функції ƒ та ƒ мають первісні на проміжку Δ, а λ та λ - дійсні числа, причому λ²+λ² > 0, то функція λƒ + λƒ також має первісну на проміжку Δ, причому ∫(λƒ(х) + λƒ(х)dх) = λ∫ƒ(х)dх + λ∫ƒ(х)dх.

2. Теорема.(формула інтегрування підстановкою). Нехай функції ƒ(x) та g(t) визначені відповідно на проміжках Δта Δ, причому g(Δ) Δ. Якщо функція ƒ має на Δ первісну F(х), тобто ∫ƒ(х)dх = F(х) + С, а функція g диференційована на Δ, то функція ƒ(g(t))g′(t) має на Δ первісну F(g(t)) та ∫ƒ(g(t))g′(t)dt = ∫ƒ(х)dx|.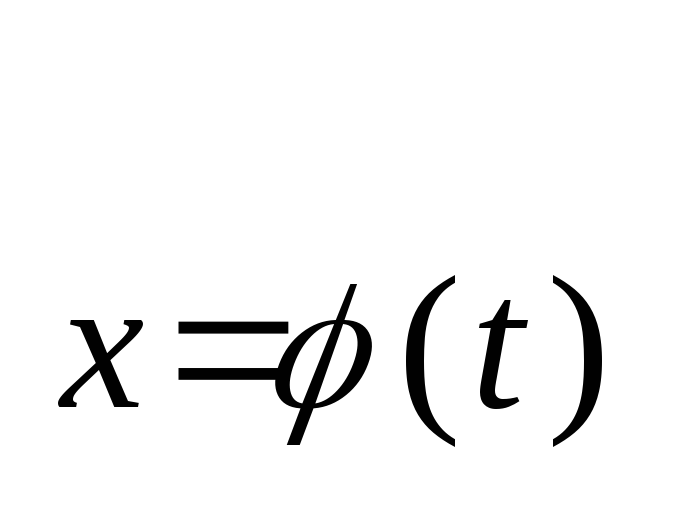

Обчислення інтегралу виду можливо зробити підстановкою u = φ(х): .

Часто формулу ∫ƒ(g(t))g′(t)dt = ∫ƒ(х)dx| використовують у зворотному напрямку, тобто справа на ліво. Маємо ∫ƒ(х)dx = ∫ƒ(g(t))g′(t)dt|; формула називається формулою інтегрування заміною змінної.

Приклад.

Обчислити інтеграл . Для цього зробимо заміну x = sint, -π/2 < t < π/2.

Маємо:

=.

3. Теорема.(формула інтегрування за частинами.) Якщо функції u(х) та v(х) диференційовані на деякому проміжку та на ньому існує інтеграл ∫vdu, то на ньому існує інтеграл ∫udv, причому ∫udv = uv - ∫vdu.

Приклад.

Обчислити інтеграл . Для обчислення інтегралу положимо: u = lnх, dv = хdх, тоді du = , v = . маємо:

.

Метод безпосереднього інтегрування

Метод інтегрування, при якому даний інтеграл шляхом тотожних перетворень підінтегральної функції (або виразу) і застосування властивостей невизначеного інтеграла зводиться до одного або декількох табличних інтегралів, називається безпосереднім інтегруванням.

При зведенні даного інтеграла до табличного часто використовуються наступні перетворення диференціала (операція «приведення під знак диференціала»):

, – число

, – число

,

,

,

,

.

Взагалі, , ця формула дуже часто використовується при обчисленні інтегралів.

Приклади:

1)

2)

3)

4)

5)

6)

7)

8)

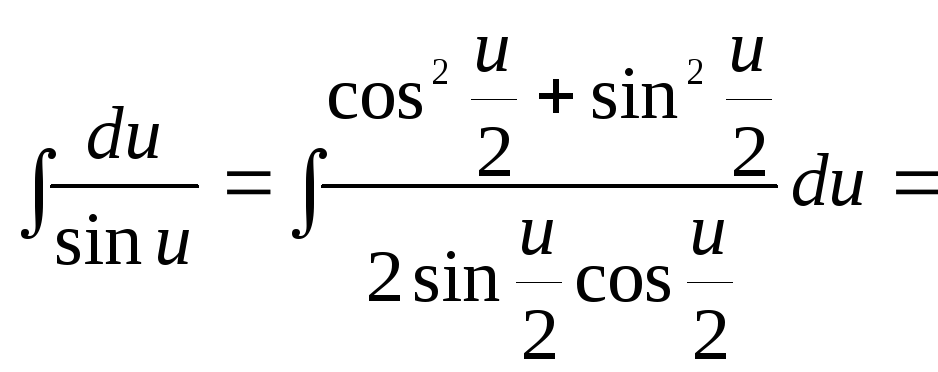
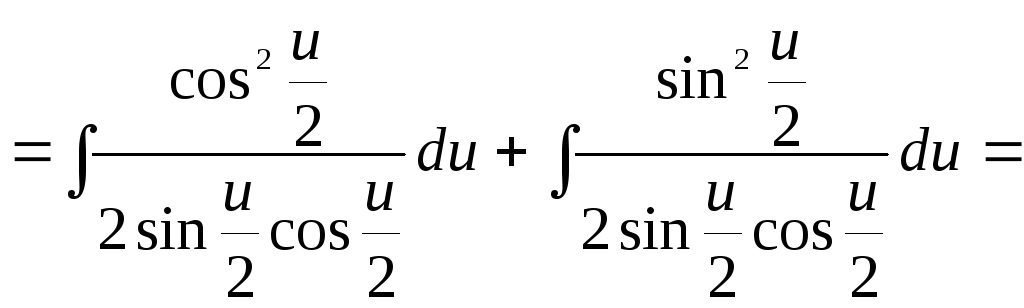
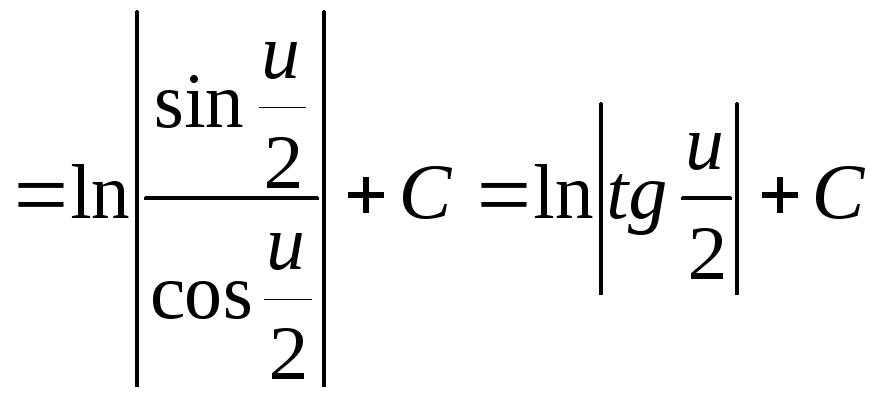
9)

10)

11)

12)

13)

.

Метод інтегрування підстановкою (заміна змінної)

Інтегрування методом підстановки полягає у введенні нової змінної інтегрування (тобто підстановкою). При цьому заданий інтеграл приводиться до нового інтеграла, який є табличним або таким, що зводиться до нього.

Нехай потрібно обчислити інтеграл . Зробимо підстановку , де – функція, що має неперервну похідну.

Тоді і на підставі властивості інваріантності формули інтеграції невизначеного інтеграла отримуємо формулу інтегрування підстановкою

(2.1)

Формула (2.1) також називається формулою заміни змінних в невизначеному інтегралі. Після знаходження інтеграла правої частини цієї рівності слід перейти від нової змінної інтеграції назад до змінної .

Іноді доцільно підбирати підстановку у вигляді , тоді , де . Іншими словами, формулу (2.1) можна застосовувати справа наліво.

Приклад 1. Знайти .

 Покладемо , тоді . Отже . 

Приклад 2. Знайти .

 Нехай , тоді , . Тому

.

Приклад 3. Отримати формулу .

Позначимо (підстановка Ейлера). Тоді , тобто .

Звідси

.

Отже

. 

Приклад 4. Знайти .

 Нехай . Тоді , . Маємо:

. 

Приклад 5. Знайти .

 Позначимо . Тоді , . Отже

. 

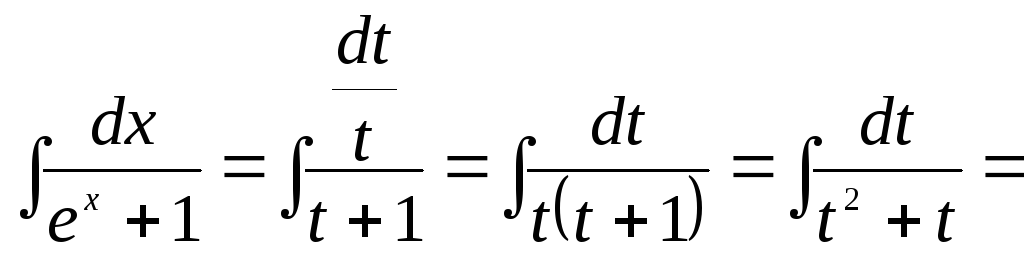
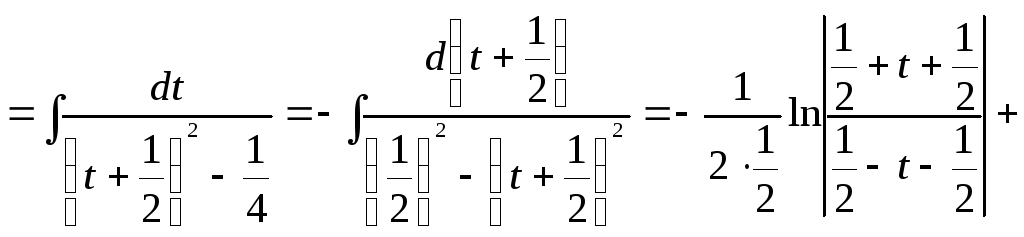
Метод інтегрування частинами

Нехай і - функція, що має неперервні похідні. Тоді . Проінтегрувавши цю рівність, отримаємо

або

Отримана формула називається формулою інтегрування частинами. Вона дає можливість звести обчислення інтеграла до обчислення інтеграла , який може виявитися істотно простішим за початковий.

Інтегрування частинами полягає в тому, що підінтегральний вираз заданого інтеграла представляється яким-небудь чином у вигляді добутку двох співмножників і (це, як правило, можна здійснити декількома способами); потім, після знаходження і використовується формула інтегрування частинами. Іноді цю формулу потрібно використовувати кілька разів.

Вкажемо деякі типи інтегралів, які зручно обчислювати методом інтегрування частинами.

1. Інтеграл вигляду 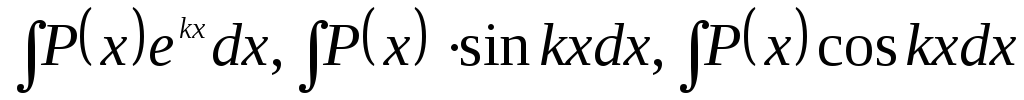, де 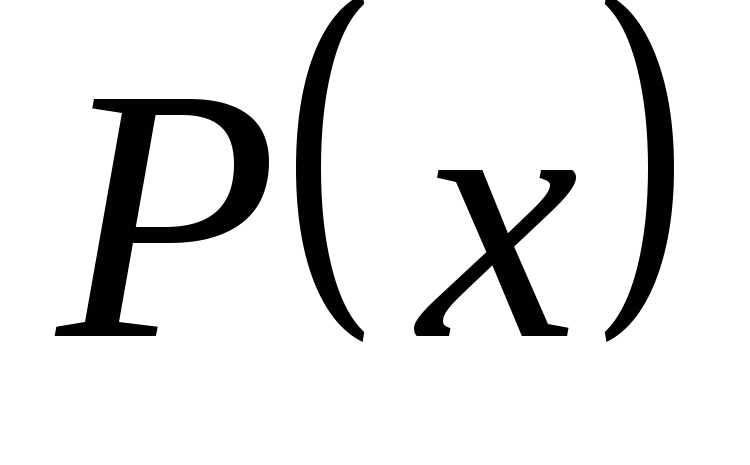- многочлен, 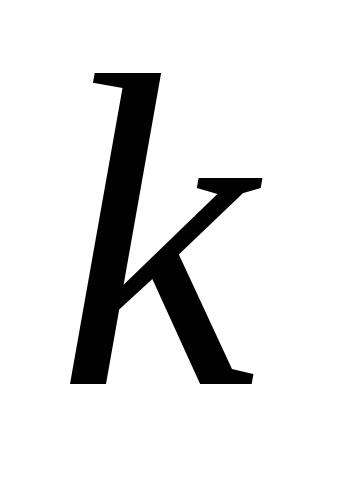– число. Зручно покласти 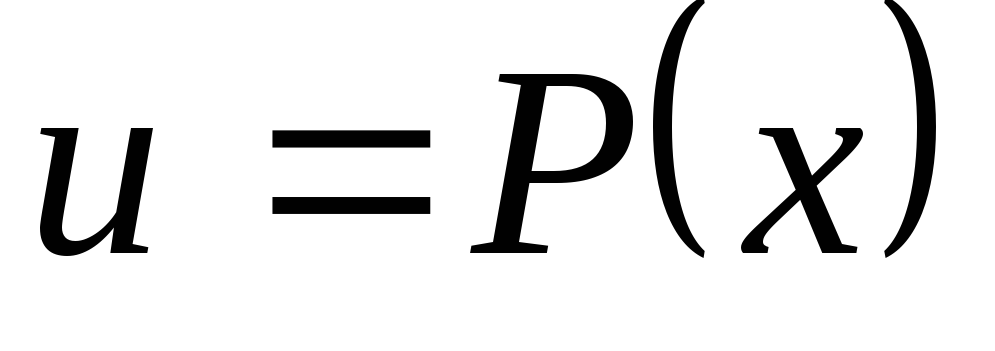, а за позначити решту співмножників.

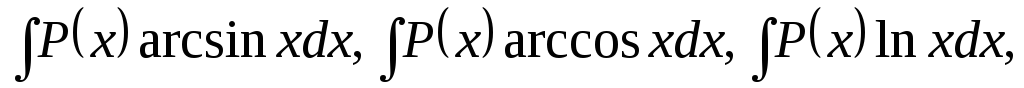
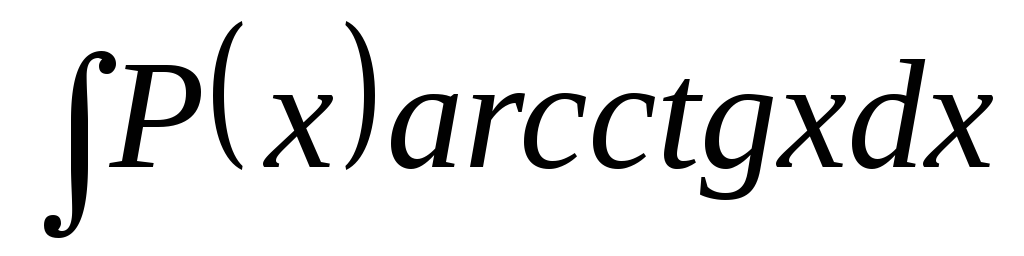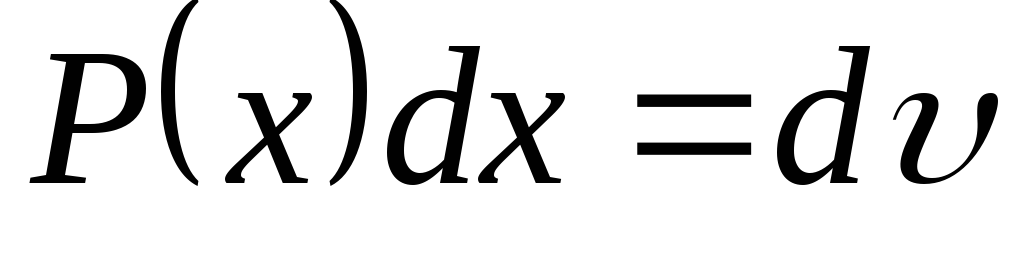2. Інтеграли вигляду . Зручно покласти , а за позначити решту співмножників.

3. Інтеграли вигляду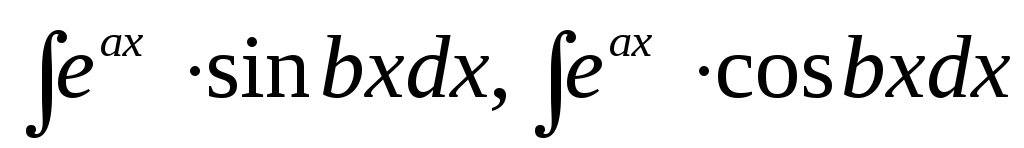, де і 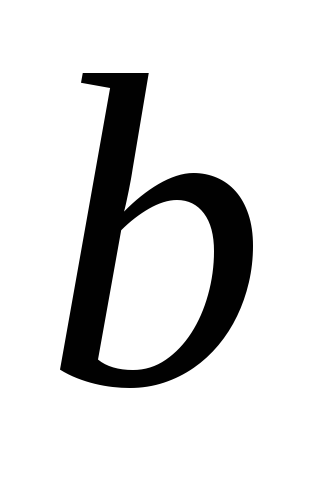– числа. За можна прийняти функцію .

Приклад 6. Знайти .

 Нехай 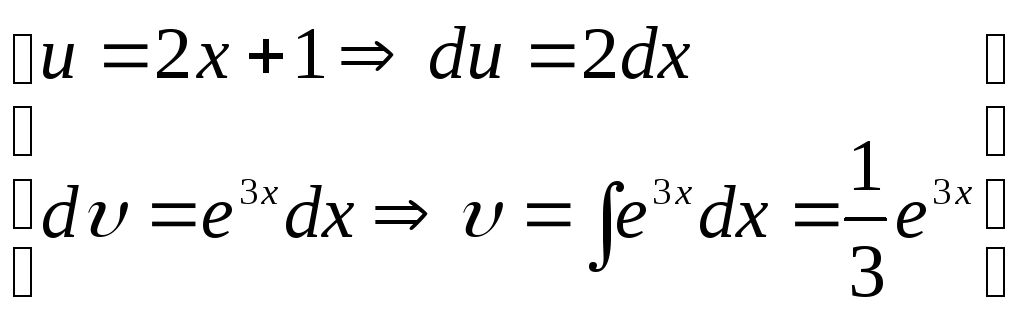. Отже, по формулі інтегрування частинами:

. 

Приклад 7. Знайти .

 Нехай 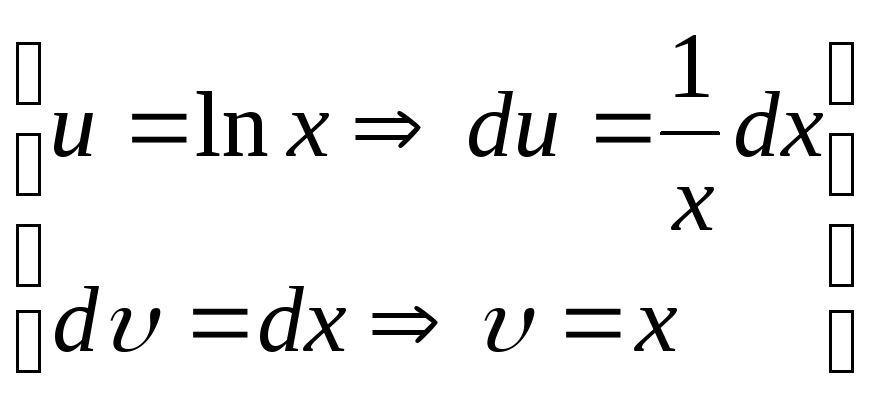. Тому

.

Приклад 8. Знайти .

 Нехай 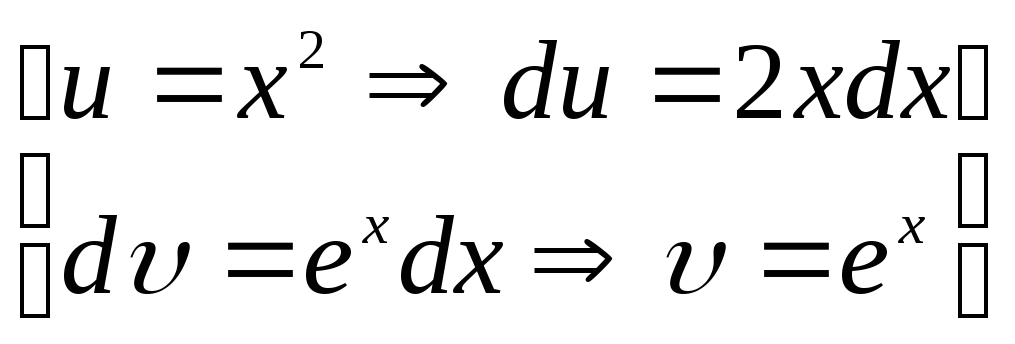. Тому

. (2.2)

Для обчислення інтеграла знову застосуємо метод інтегрування частинами: . Значить

. (2.3)

Тому .

Приклад 9. Знайти .

 Нехай 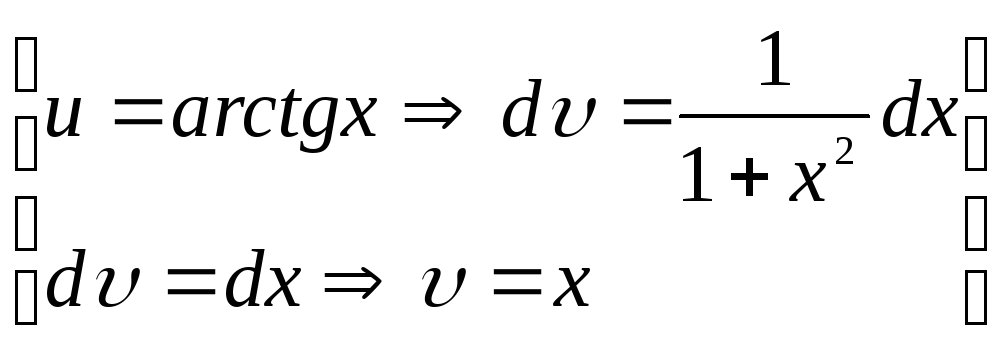. Тому

.