
матан 3 курс 2013 / лекции / Невизначений інтеграл / лекция № 8
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ЛЕКЦІЯ № 8
з теми: «Інтегрування функції методом заміни змінної.»
Модуль КЗН-02. ПР.О.03.07 Невизначений інтеграл.
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики.
Протокол № ____ від _______20__ р.
Голова циклової комісії ПМ Велікодна О. В.
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІI
Викладач: Велікодна Ольга Володимирівна.
Тема: Інтегрування функції методом заміни змінної.
Мета:
-
Дидактична: навчитися обчислювати первісну, володіти методами інтегрування, знаходити первісну раціональних функцій, трансцендентних та ірраціональних функцій.
-
Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням методики пошукової технології.
Тип: лекція
Вид: лекція – дослідження.
Методи та форми проведення заняття: словесні, наочні, пояснювально-ілюстративні, проблемно – пошукові.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань: теорема про інтегрування елементарних функцій методом заміни, таблиця похідних елементарних функцій, таблиця первісних елементарних функцій, теореми про диференціювання складної функції, правила диференціювання.
-
Вивчення нового матеріалу:
-
Тема лекції: Інтегрування функції методом заміни змінної.
-
Мотивація вивчення матеріалу: вивчити основний математичний апарат – невизначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
Конспект лекції № 8.
Тема: «Інтегрування функції методом заміни змінної.»
План лекції № 8.
-
Інтегрування функції методом заміни змінної.
-
Теорема.(формула інтегрування підстановкою). Нехай функції ƒ(x) та g(t) визначені відповідно на проміжках Δ
 та
Δ
та
Δ ,
причому g(Δ
,
причому g(Δ )
)
 Δ
Δ .
Якщо функція ƒ має на Δ
.
Якщо функція ƒ має на Δ первісну F(х), тобто ∫ƒ(х)dх = F(х) + С, а
функція g диференційована на Δ
первісну F(х), тобто ∫ƒ(х)dх = F(х) + С, а
функція g диференційована на Δ ,
то функція ƒ(g(t))g′(t) має на Δ
,
то функція ƒ(g(t))g′(t) має на Δ первісну F(g(t)) та ∫ƒ(g(t))g′(t)dt
= ∫ƒ(х)dx|
первісну F(g(t)) та ∫ƒ(g(t))g′(t)dt
= ∫ƒ(х)dx| .
.
Обчислення
інтегралу виду
![]() можливо зробити підстановкою u = φ(х):
можливо зробити підстановкою u = φ(х):
![]() .
.
Часто
формулу ∫ƒ(g(t))g′(t)dt
= ∫ƒ(х)dx|![]() використовують
у зворотному
напрямку, тобто справа на ліво. Маємо
∫ƒ(х)dx
= ∫ƒ(g(t))g′(t)dt|
використовують
у зворотному
напрямку, тобто справа на ліво. Маємо
∫ƒ(х)dx
= ∫ƒ(g(t))g′(t)dt|![]() ;
формула
називається формулою
інтегрування заміною змінної.
;
формула
називається формулою
інтегрування заміною змінної.
Приклад.
Обчислити
інтеграл
![]() .
Для цього зробимо заміну x = sint, -π/2 <
t < π/2.
.
Для цього зробимо заміну x = sint, -π/2 <
t < π/2.
Маємо:
![]()
=![]() .
.
Приклад
1.
Знайти
![]() .
.
Покладемо
![]() ,
тоді
,
тоді
![]() .
Отже
.
Отже
![]() .
.
Приклад
2.
Знайти
![]() .
.
Нехай
![]() ,
тоді
,
тоді
![]() ,
,
![]() .
Тому
.
Тому
![]()
![]()
![]() .
.
Приклад
3.
Отримати формулу
![]() .
.
Позначимо
![]() (підстановка
Ейлера).
Тоді
(підстановка
Ейлера).
Тоді
![]() ,
тобто
,
тобто
![]() .
.
Звідси
![]() .
.
Отже
![]() .
.
Приклад
4.
Знайти
![]() .
.
Нехай
![]() .
Тоді
.
Тоді
![]() ,
,
![]() .
Маємо:
.
Маємо:
![]()
![]() .
.
Приклад
5.
Знайти
![]() .
.
Позначимо
![]() .
Тоді
.
Тоді
![]() ,
,
![]() .
Отже
.
Отже
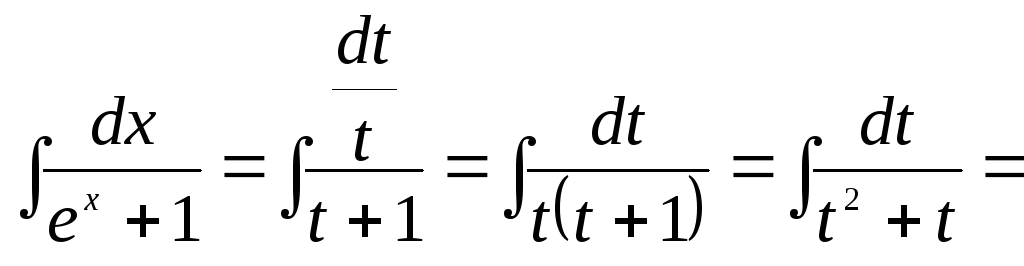
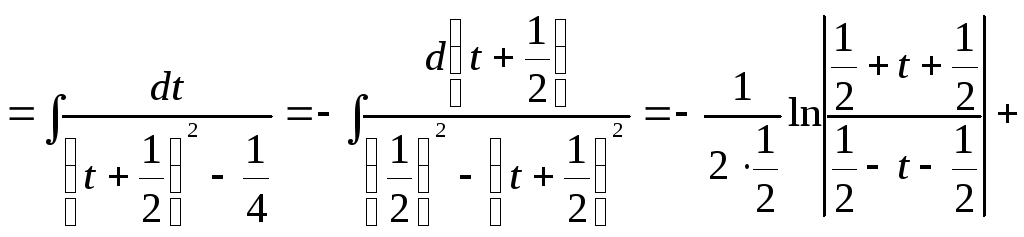
![]() .
.
Приклад 6.
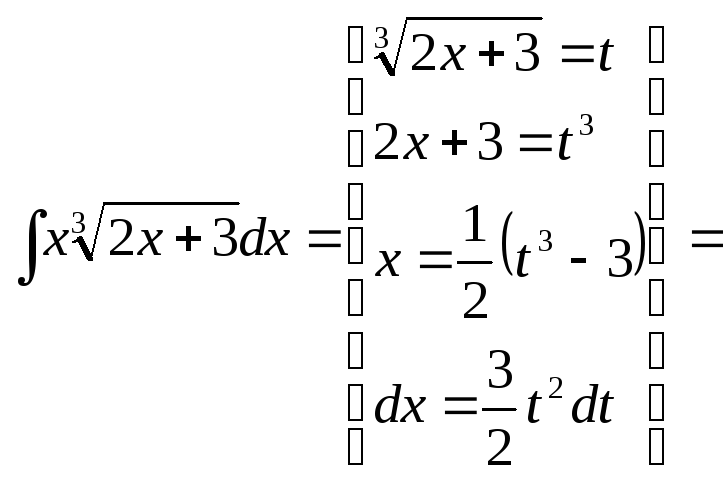
![]() =
=
=![]()
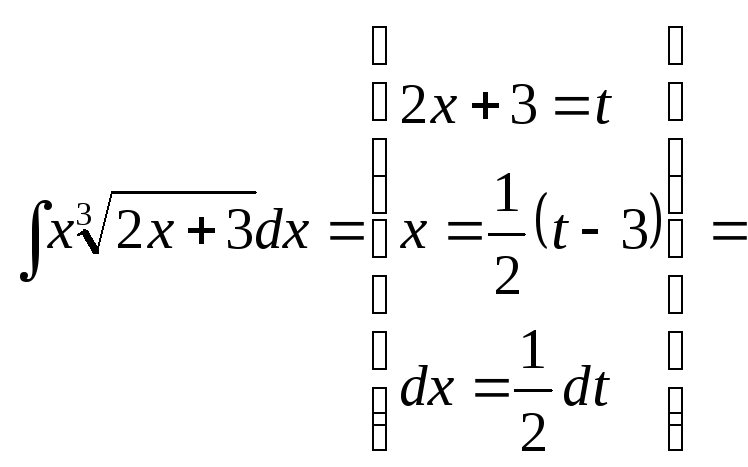
![]()
=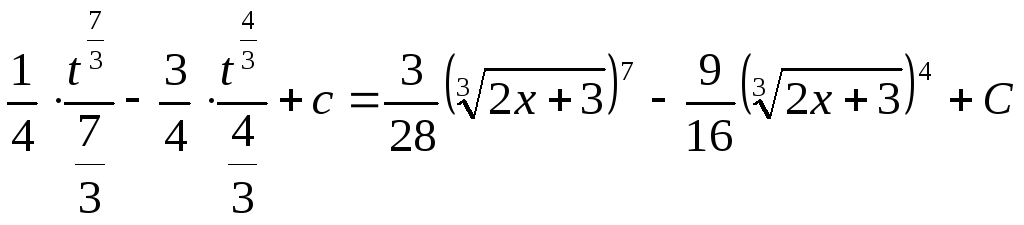 ;
;
Із цього прикладу видно, як дві різні підстановки приводять до інтегралів різної складності але з однаковим кінцевим результатом.
Приклад 7. Знайти інтеграл.

Приклад 8. Знайти інтеграл.
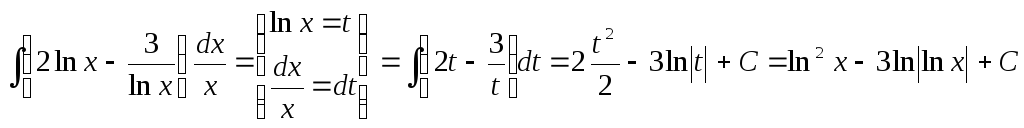 ;
;
Приклад 9. Знайти інтеграл.
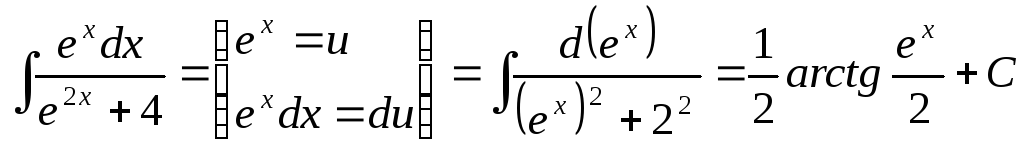
Тут
використана заміна
![]() і формула 11 табличних інтегралів.
і формула 11 табличних інтегралів.
