
матан 3 курс 2013 / лекции / Невизначений інтеграл / лекция № 6
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ЛЕКЦІЯ № 6
з теми: «Інтегрування трансцендентних функцій.»
Модуль КЗН-02. ПР.О.03.07 Невизначений інтеграл.
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики.
Протокол № ____ від _______20__ р.
Голова циклової комісії ПМ Велікодна О. В.
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІI
Викладач: Велікодна Ольга Володимирівна.
Тема: Інтегрування трансцендентних функцій.
Мета:
-
Дидактична: навчитися обчислювати первісну, володіти методами інтегрування, знаходити первісну раціональних функцій, трансцендентних та ірраціональних функцій.
-
Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням методики пошукової технології.
Тип: лекція
Вид: лекція – дослідження.
Методи та форми проведення заняття: словесні, наглядні, проблемно – пошукові.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань: визначення трансцендентних функцій, їх види та властивості, таблиця інтегралів, методи інтегрування.
-
Вивчення нового матеріалу:
-
Тема лекції: Інтегрування трансцендентних функцій.
-
Мотивація вивчення матеріалу: вивчити основний математичний апарат – невизначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
Конспект лекції № 6.
Тема: «Інтегрування трансцендентних функцій.»
План лекції № 6.
-
Інтеграли виду
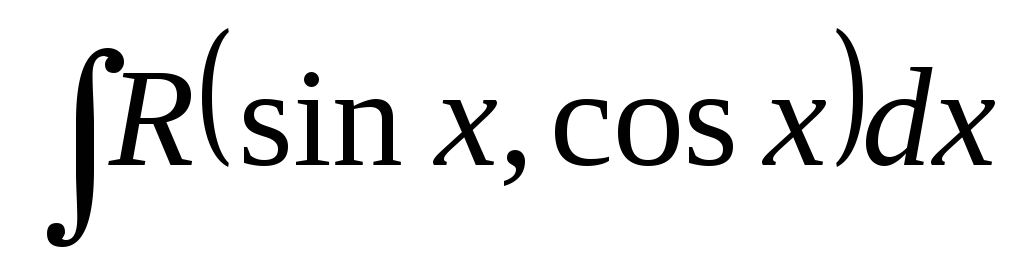 .
. -
Інтеграли виду
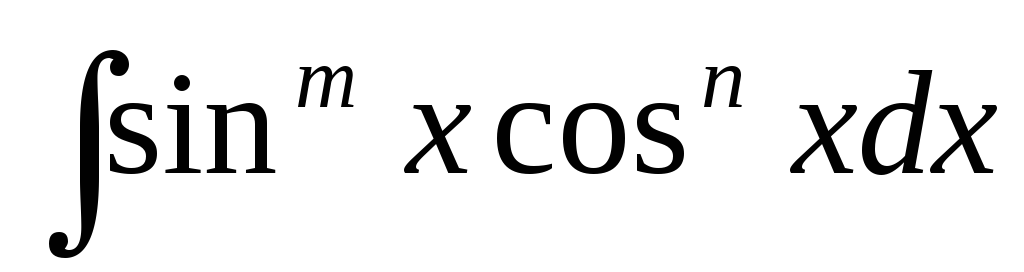 .
. -
Інтеграли виду
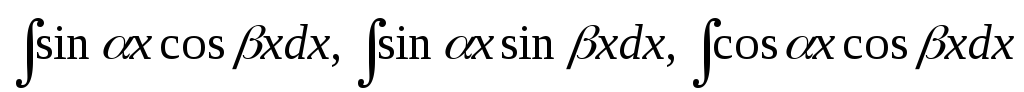 .
.
-
Інтеграли виду
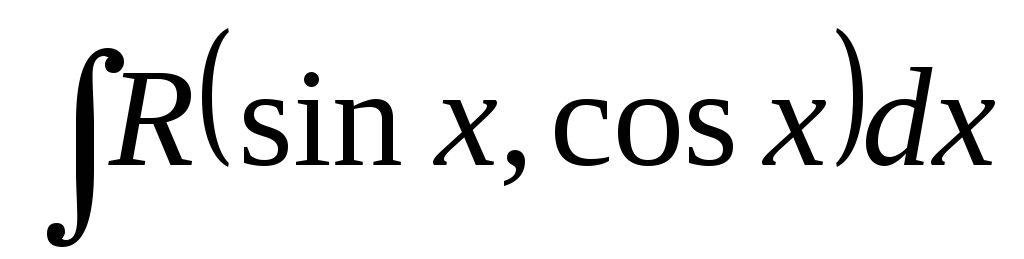 зводиться підстановкою
зводиться підстановкою
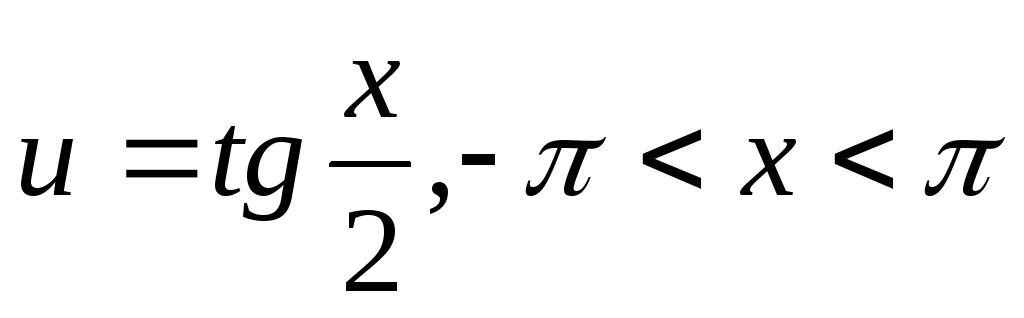 до інтегралу від раціональної функції.
Користуючись формулами універсальної
підстановки, маємо:
до інтегралу від раціональної функції.
Користуючись формулами універсальної
підстановки, маємо:
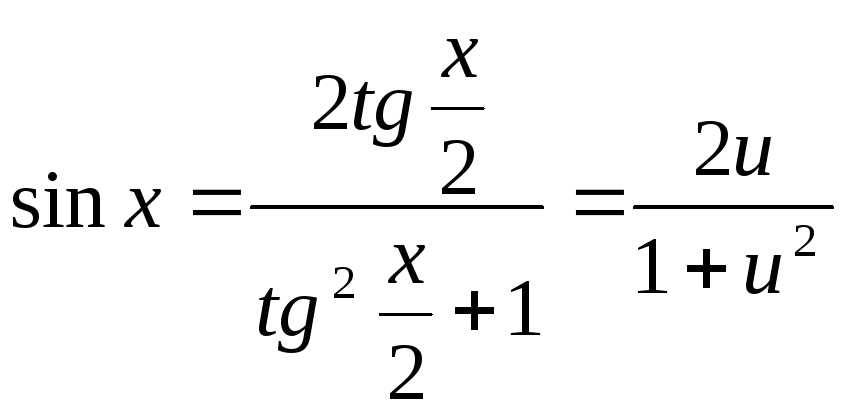 ,
,
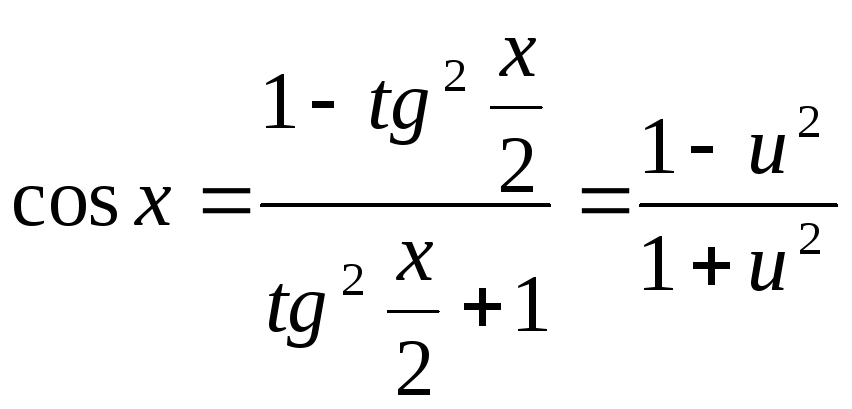 .
Тоді маємо:
.
Тоді маємо:
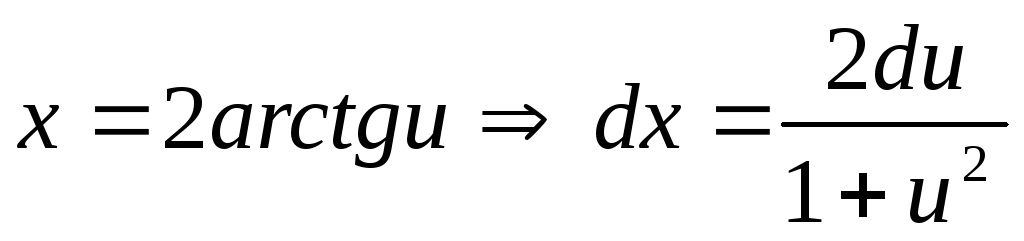 .
Підставляючи отримані вирази в даний
інтеграл, маємо:
.
Підставляючи отримані вирази в даний
інтеграл, маємо:
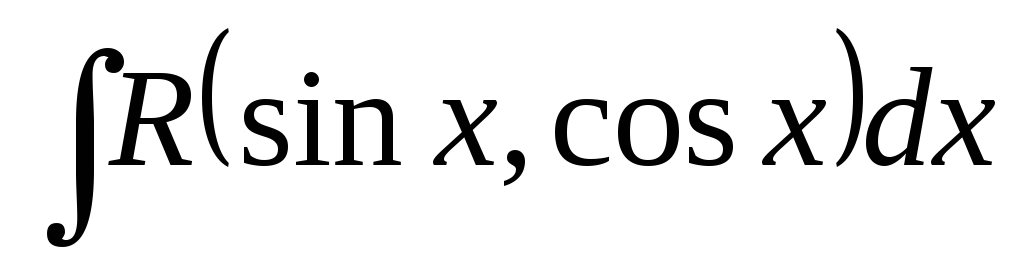 =
=
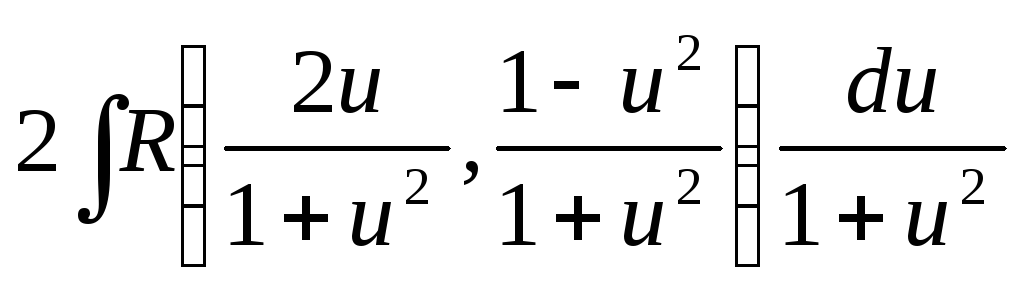 ,
тобто отримали інтеграл від раціональної
функції. Також при обчисленні інтегралів
типу
,
тобто отримали інтеграл від раціональної
функції. Також при обчисленні інтегралів
типу
 часто доцільно використовувати
підстановки
часто доцільно використовувати
підстановки
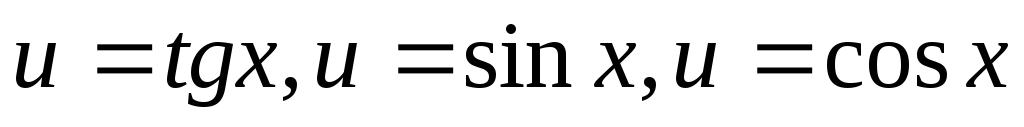 .
В деяких випадках інтегрування за
допомогою цих підстановок надає
можливість проводити менше обчислень,
ніж при використанні універсальних
підстановок.
.
В деяких випадках інтегрування за
допомогою цих підстановок надає
можливість проводити менше обчислень,
ніж при використанні універсальних
підстановок. -
Інтеграли виду
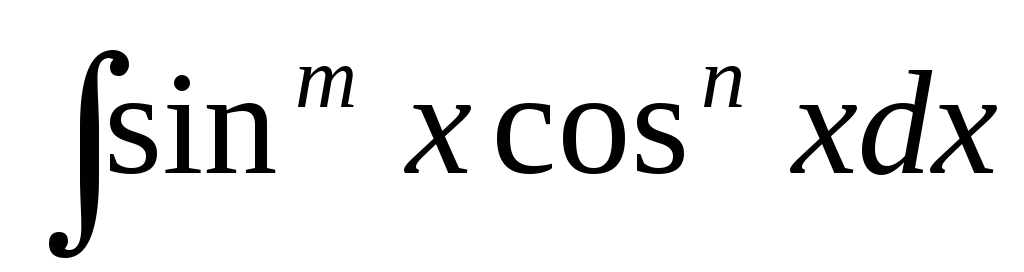 обчислюються в залежності від ступенів
n та m. Розглянемо можливі випадки.
обчислюються в залежності від ступенів
n та m. Розглянемо можливі випадки.
-
n та m – раціональні числа. Тоді підстановкою
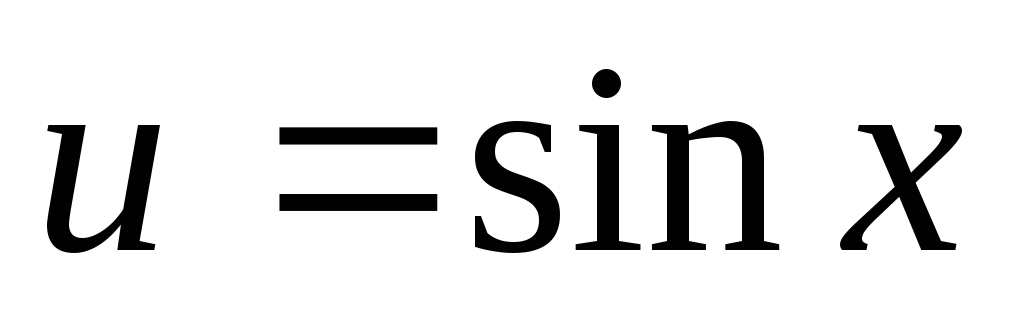 чи
чи
 інтеграл
інтеграл
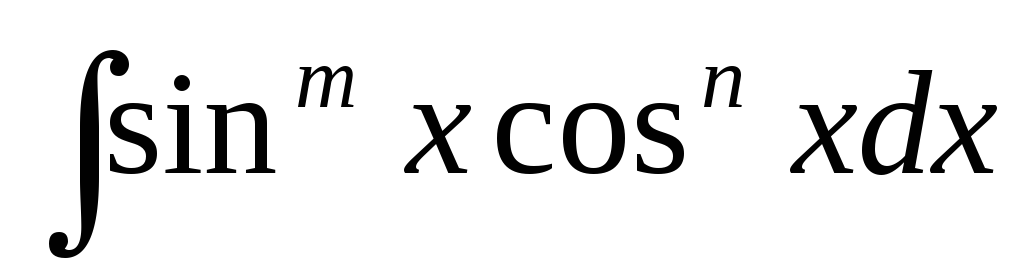 зводиться до виду інтеграла від
диференційного біному. Дійсно, якщо
зводиться до виду інтеграла від
диференційного біному. Дійсно, якщо
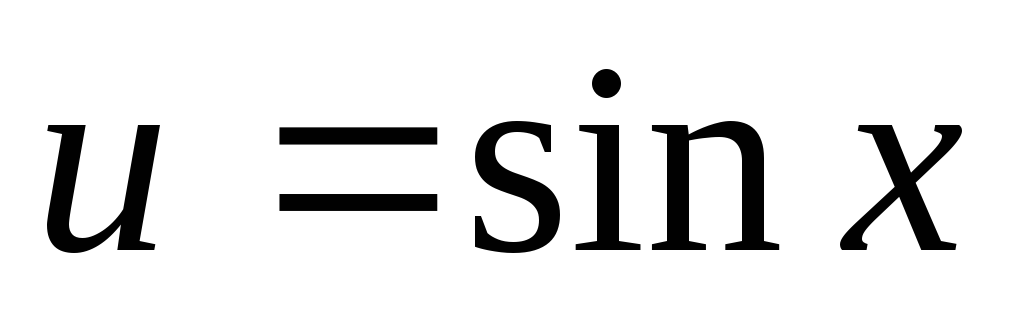 ,
то
,
то
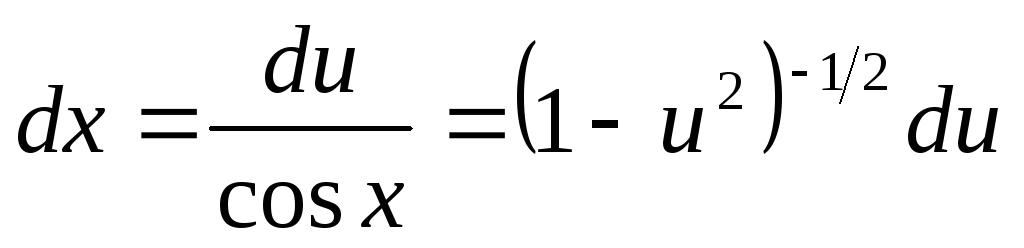 .
Тоді
.
Тоді
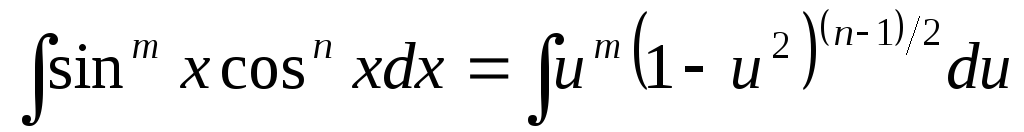 .
. -
якщо n та m – цілі числа, причому n – парне, m – непарне, то вводимо заміну
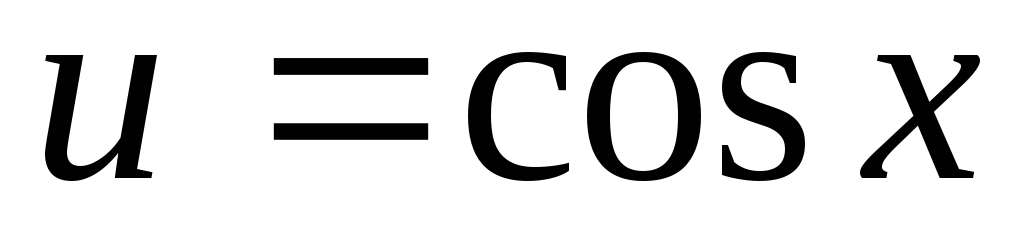 та використовуємо основну тригонометричну
тотожність
та використовуємо основну тригонометричну
тотожність
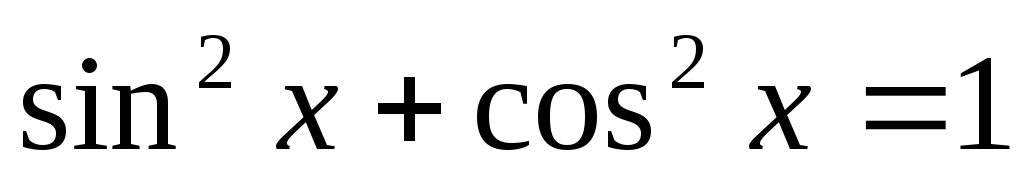 .
Дійсно, маємо
.
Дійсно, маємо
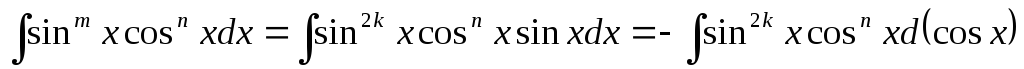 =
=
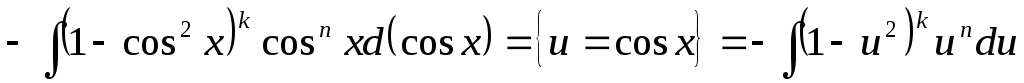 .
Таким чином, отримали інтеграл від
раціональної функції.
.
Таким чином, отримали інтеграл від
раціональної функції. -
якщо n та m – цілі числа, причому n – непарне, m –парне, то вводимо заміну
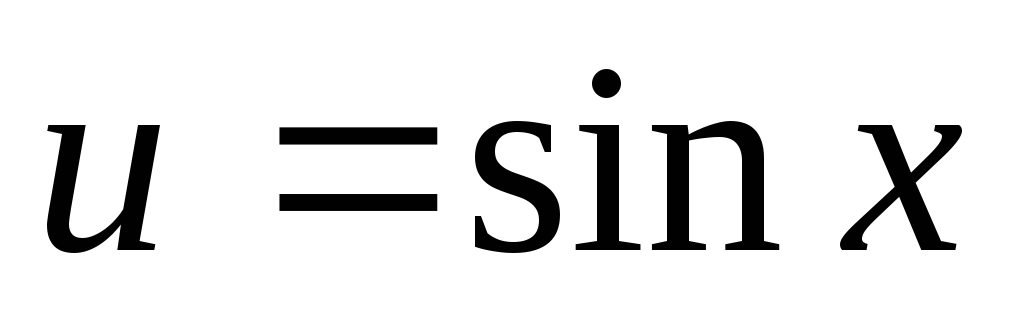 та використовуємо основну тригонометричну
тотожність
та використовуємо основну тригонометричну
тотожність
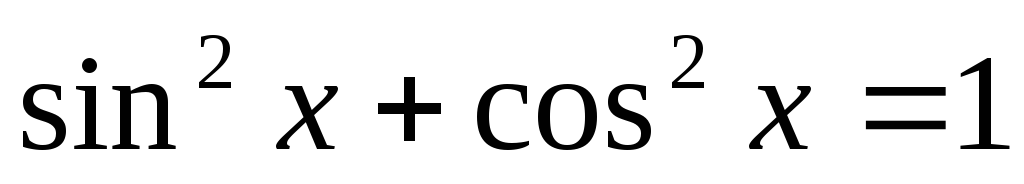 .
Дійсно, маємо
.
Дійсно, маємо
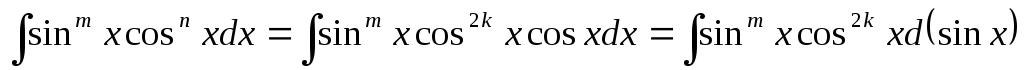 =
=
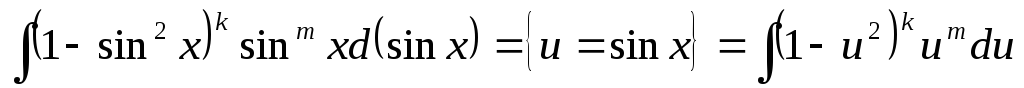 .
Таким чином, отримали інтеграл від
раціональної функції.
.
Таким чином, отримали інтеграл від
раціональної функції. -
якщо n та m – цілі числа, причому n – непарне, m –непарне, тобто n = 2k + 1, m = 2l + 1, то вводимо заміну
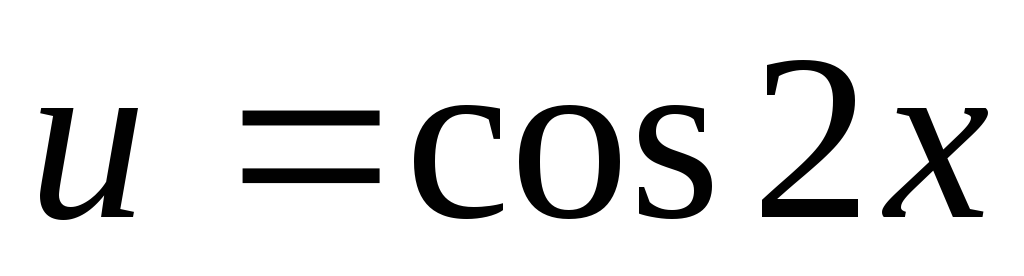 . Дійсно,
. Дійсно,
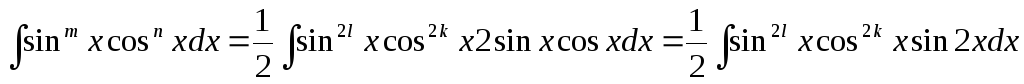 =
=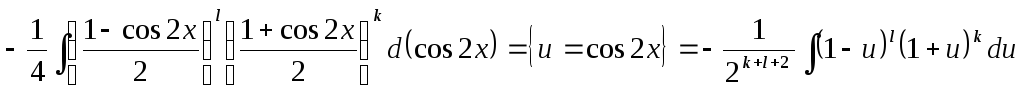 Таким чином, отримали інтеграл від
раціональної функції(k та l можуть бути
від’ємними).
Таким чином, отримали інтеграл від
раціональної функції(k та l можуть бути
від’ємними). -
якщо n та m – цілі числа, причому n –парне, m –парне, тобто n = 2k, m = 2l, то вводимо заміну
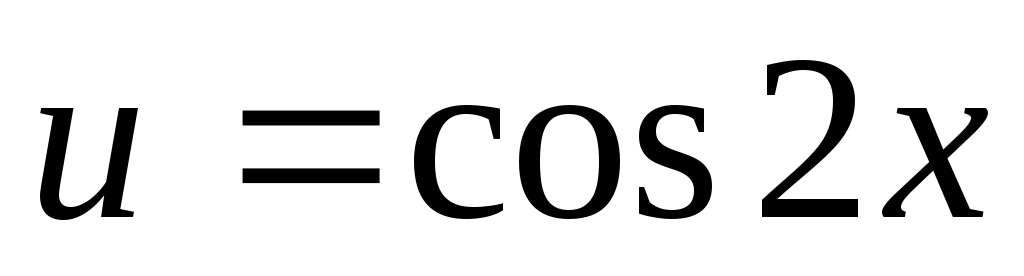 чи заміну
чи заміну
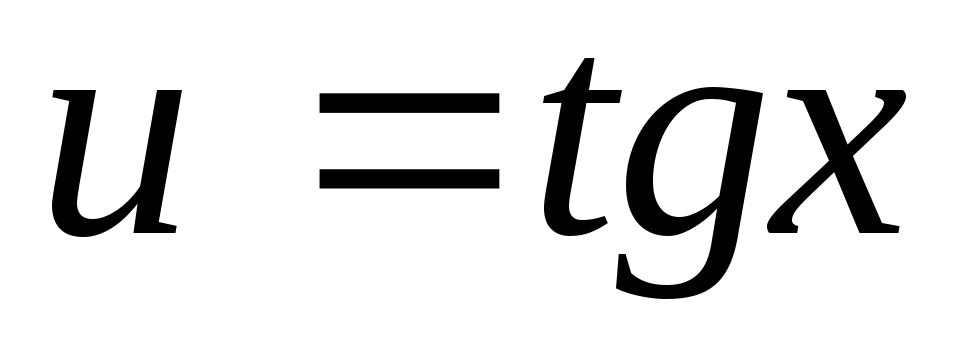 ,
та користуємось формулами зниження
ступеня:
,
та користуємось формулами зниження
ступеня:
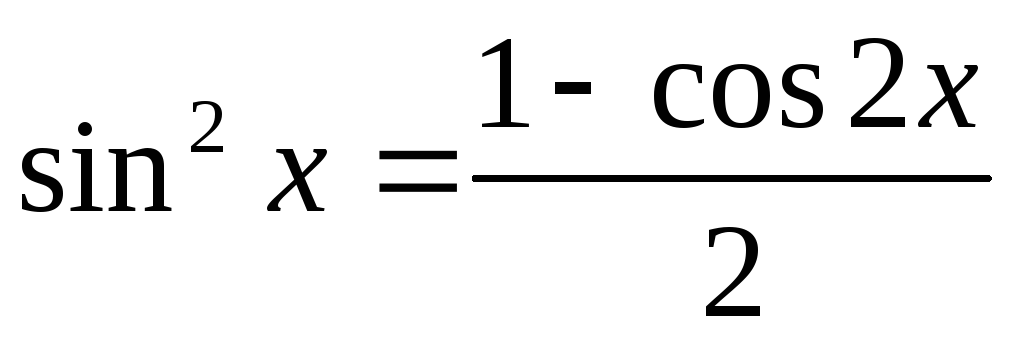 ,
,
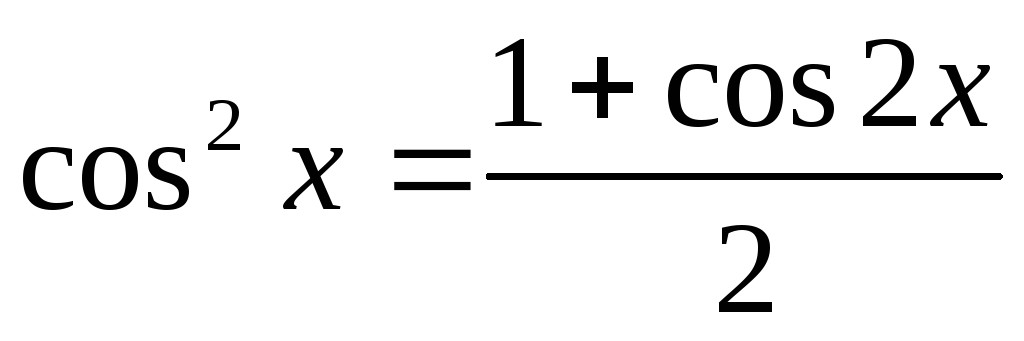 .
При цьому отримаємо інтеграл того ж
типу, але від функцій нижчого ступеня.
.
При цьому отримаємо інтеграл того ж
типу, але від функцій нижчого ступеня.
-
Інтеграли виду
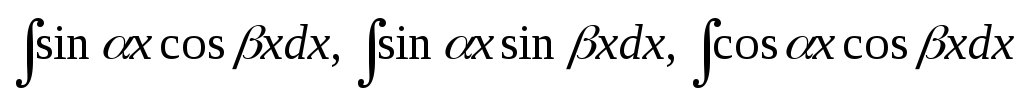 обчислюються, якщо їх підінтегральні
вирази спростити за формулами:
обчислюються, якщо їх підінтегральні
вирази спростити за формулами:
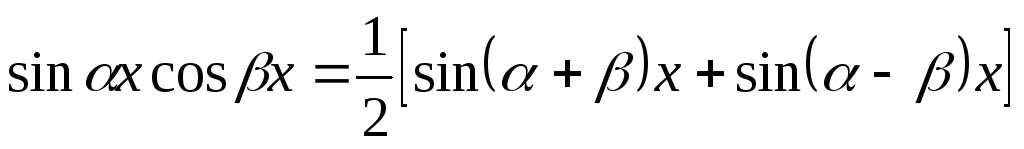 ;
;
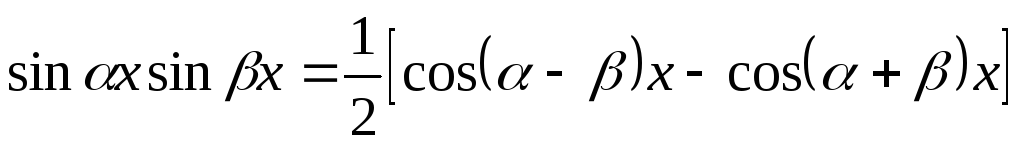 ;
;
 .
.
Універсальна тригонометрична підстановка
Розглянемо деякі
випадки знаходження інтеграла від
тригонометричних функцій. Функцію із
змінними
![]() і
і
![]() ,
над якими виконуються раціональні дії
(додавання, віднімання, множення і
ділення) прийнято позначати
,
над якими виконуються раціональні дії
(додавання, віднімання, множення і
ділення) прийнято позначати
![]() ,
де
,
де
![]() – знак раціональної функції.
– знак раціональної функції.
Обчислення
невизначених інтегралів типу
![]() зводиться до обчислення інтегралів від
раціональної функції підстановкою
зводиться до обчислення інтегралів від
раціональної функції підстановкою
![]() ,
яка називається універсальною.
,
яка називається універсальною.
Дійсно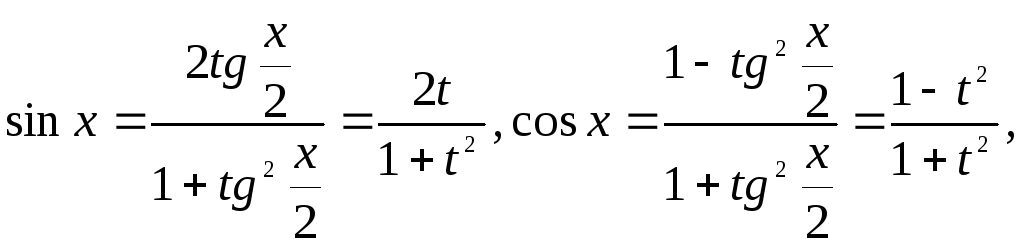
![]() .
.
Тому
![]()
де
![]() - раціональна функція від
- раціональна функція від
![]() .
Звичайно, цей спосіб досить громіздкий,
зате він завжди приводить до результату.
.
Звичайно, цей спосіб досить громіздкий,
зате він завжди приводить до результату.
На практиці застосовують і інші, більш прості підстановки, залежно від властивостей (і вигляду) підінтегральної функції. Зокрема, зручні наступні правила:
1) якщо
функція
![]() непарна відносно
непарна відносно
![]() ,
тобто
,
тобто
![]() ,
то підстановку
,
то підстановку
![]() раціоналізує
інтеграл;
раціоналізує
інтеграл;
2) якщо
функція
![]() непарна відносно
непарна відносно
![]() ,
тобто
,
тобто
![]() ,
то виконується підстановка
,
то виконується підстановка
![]() ;
;
3) якщо
функція
![]() парна відносно
парна відносно
![]() і
і
![]() ,
тобто
,
тобто
![]() ,
то інтеграл раціоналізується підстановкою
,
то інтеграл раціоналізується підстановкою
![]() .
Така ж підстановка застосовується, якщо
інтеграл має вигляд
.
Така ж підстановка застосовується, якщо
інтеграл має вигляд
![]() .
.
Приклад
1.
Знайти інтеграл
![]()
Зробимо
універсальну підстановку
![]() .
Тоді,
.
Тоді,
![]() .
Отже
.
Отже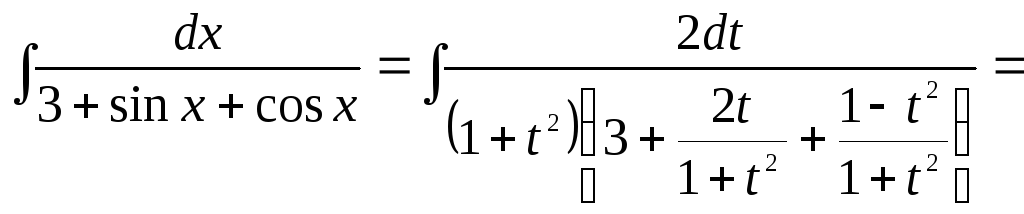
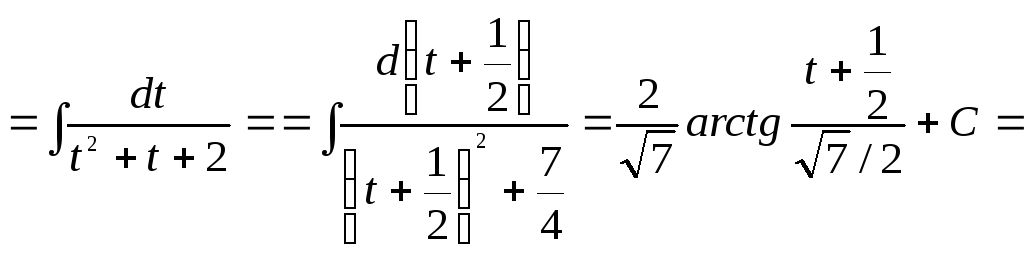
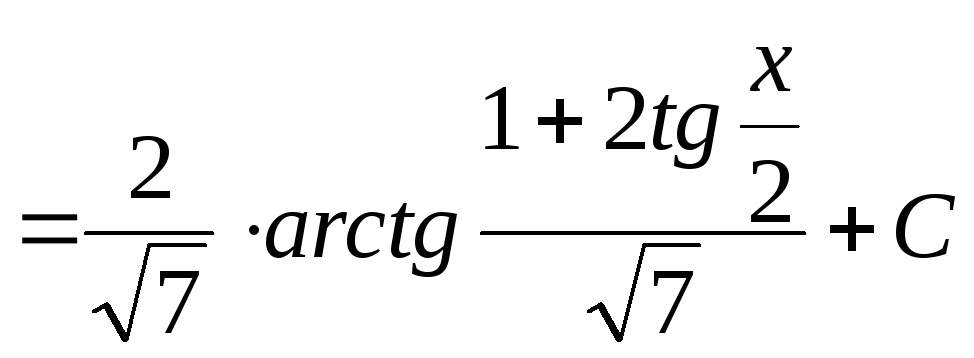 .
.
Приклад
2.
Знайти інтеграл
![]() .
.
Оскільки
![]()
![]() ,
то вважаємо
,
то вважаємо
![]() .
Звідси
.
Звідси
![]() ,
,
![]() і
і
![]() .
.
Тому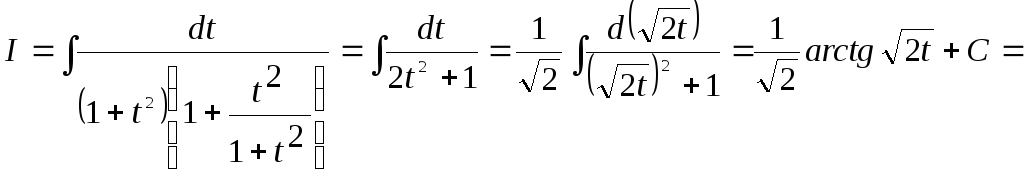
![]() .
.
Інтеграли
виду
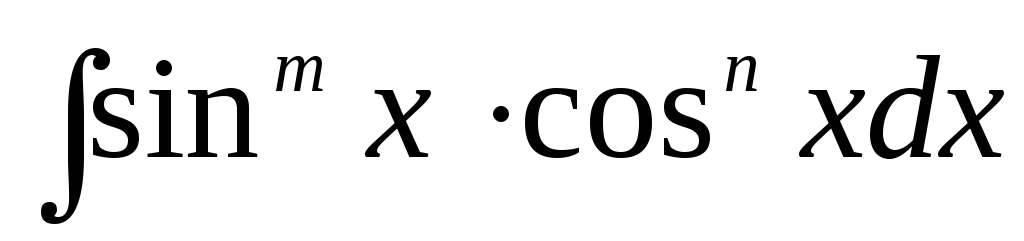
Для знаходження таких інтегралів використовуються наступні прийоми:
1)
підстановка
![]() ,
якщо
,
якщо
![]() – ціле додатне непарне число;
– ціле додатне непарне число;
2)
підстановка
![]() ,
якщо
,
якщо
![]() – ціле додатне непарне число;
– ціле додатне непарне число;
3) формули
пониження порядку:
![]()
![]()
![]() ,
якщо
,
якщо
![]() і
і
![]() - цілі невід’ємні парні числа;
- цілі невід’ємні парні числа;
4)
підстановка
![]() ,
якщо
,
якщо
![]() –
є парне від’ємне ціле число.
–
є парне від’ємне ціле число.
Приклад
3.
Знайти інтеграл
![]() .
.
Застосуємо
підстановку
![]() .
Тоді
.
Тоді
![]() ,
,
![]() і
і
![]()
![]()
![]() .
.
Приклад
4.
Знайти інтеграл
![]() .
.
![]()
![]()
![]() .
.
Приклад
5.
Знайти інтеграл
![]() .
.
Тут
![]() .
Позначимо
.
Позначимо
![]() .
Тоді
.
Тоді
![]() ,
,
![]() і
і

![]() .
.
Використання тригонометричних перетворень
Інтеграли
типу
![]() ,
,
![]() ,
,
![]() обчислюються за допомогою відомих
тригонометричних формул:
обчислюються за допомогою відомих
тригонометричних формул:
![]() ,
,
![]() ,
,
![]() .
.
Приклад
6.
Знайти інтеграл
![]() .
.
![]()
![]() .
.
