
матан 3 курс 2013 / лекции / Визначений інтеграл / лекция № 15
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ЛЕКЦІЯ № 15
з теми: «Геометричний зміст визначеного інтеграла.»
Модуль КЗН-02. ПР.О.03.08 Визначений інтеграл
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики.
Протокол № ____ від _______20__ р.
Голова циклової комісії ПМ Велікодна О. В.
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІІ
Викладач: Велікодна Ольга Володимирівна.
Тема: Геометричний зміст визначеного інтеграла.
Мета:
-
Дидактична: навчитись застосовувати таблицю первісних для знаходження інтеграла Ньютона – Лейбніца, володіти методами інтегрування, досліджувати функцію на інтегрованість за Ріманом, застосовувати інтеграл Рімана при розв'язанні задач геометрії, механіки та фізики.
-
Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.
-
Методична: вдосконалювати методику проведення лекції з використанням методики пошукової технології.
Тип: лекція
Вид: лекція – діалог.
Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.
Науково-методичне забезпечення:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
Між предметні зв’язки:
-
Дисципліни, що забезпечують: елементарна математика
-
Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.
Обладнання: зошити, ручки, крейда, дошка.
ХІД ЗАНЯТТЯ.
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Актуалізація опорних знань: визначення первісної, визначення невизначеного інтегралу, таблиця інтегралів основних елементарних функцій, класи функцій, що інтегруються, методи інтегрування. Визначення границі функції в точці, властивості границі функції в точці. Визначення інтегралу Рімана, методи інтегрування у визначеному інтегралі, формула Ньютона-Лейбніца.
-
Вивчення нового матеріалу:
-
Тема лекції: Геометричний зміст визначеного інтеграла.
-
Мотивація вивчення матеріалу: вивчити основний математичний апарат –визначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.
-
План вивчення нового матеріалу: надається в конспекті лекції.
-
Виклад нового матеріалу. Конспект лекції надається.
-
Закріплення нового матеріалу.
-
Підсумки заняття.
-
Домашнє завдання:
Конспект лекції № 15.
Тема: Геометричний зміст визначеного інтеграла.
План лекції № 15.
-
Обчислення площі криволінійної трапеції.
-
Обчислення площі в полярних координатах.
-
Обчислення довжини кривої.
-
Площа поверхні обертання.
-
Об’єми тіла обертання.
-
Теорема. Якщо функція ƒ невід’ємна та неперервна на відрізку [a, b], а множина Р = {(х, у): a ≤ х ≤ b, 0 ≤ у ≤ ƒ(х)}, то площа множини Р виражається формулою S =
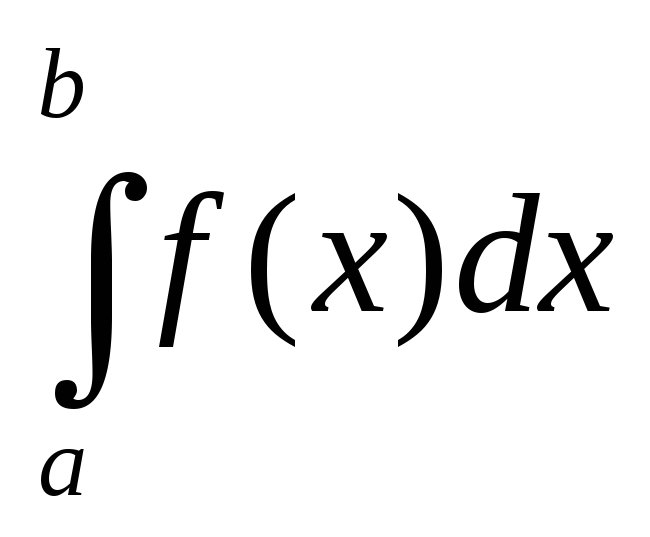 .
.
Множина Р = {(х, у): a ≤ х ≤ b, 0 ≤ у ≤ ƒ(х)} називається криволінійною трапецією, що породжена графіком функції ƒ.
Якщо
функція ƒ не додатна та неперервна на
відрізку [a, b], а множина Р = {(х, у):
a ≤ х ≤ b, ƒ(х) ≤ у ≤ 0}, то площа множини
Р виражається формулою S =
-![]() .
.
Приклад.
-
Знайти площу, що обмежена однією аркою синусоїди:
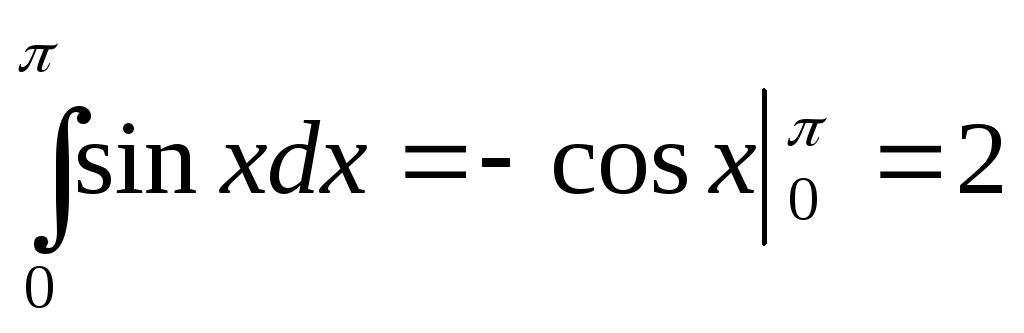 .
. -
Знайти площу S(х) криволінійної трапеції, що обмежена дугою гіперболи у = 1/х, відрізком [1, х] осі х та відповідними відрізками, паралельними до осі ОУ: S(х) =
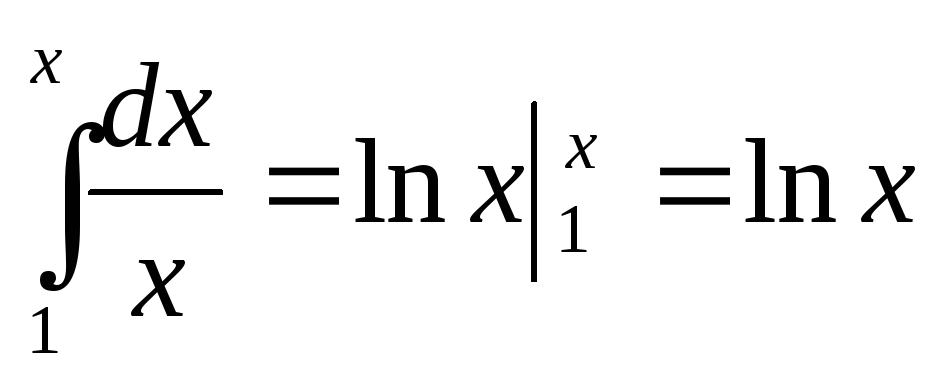 .
.
-
Нехай Р – замкнена множина, границя якого складається з деякої кривої, що задана в полярних координатах ρ = ρ(φ), α ≤ φ ≤ β, ρ(φ) – неперервна функція, та двох відрізків промінів φ = α, φ = β. Тоді площа множини Р дорівнює інтегралу S =
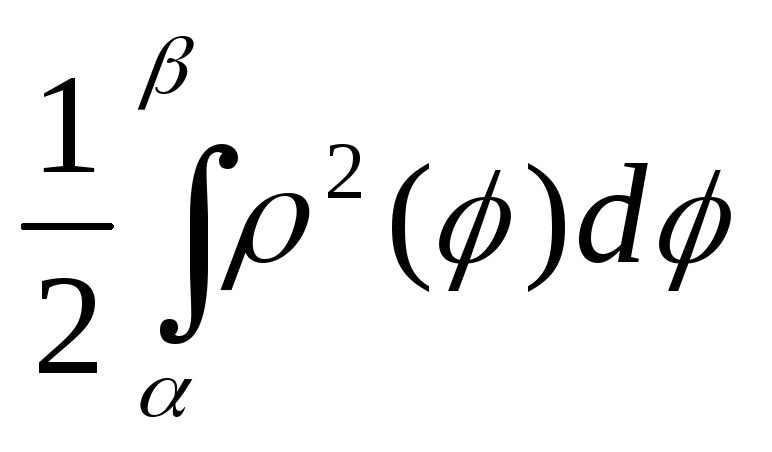 .
.
Приклад.
Знайти площу S множини, обмеженої кривою ρ = а(1 + cosφ), 0 ≤ φ ≤ 2π, що називається кардіоїдою:
S =
![]() .
.
-
Нехай Г – крива, що задана своїм неперервно диференційованим векторним представленням r = r(t), a ≤ t ≤ b; тоді вона спрямляємо, а якщо s = s(t) – її змінна довжина дуги, що відраховується від начала, то функція s(t) диференційована та s′(t) = |r′(t)|.
За формулою Ньютона - Лейбніца для довжини S кривої маємо формулу:
S =
![]() .
.
Якщо
r(t) = {х(t), у(t), z(t)}, то S =
![]() .
.
У випадку,
коли крива Г є графіком функції у = ƒ(х),
a ≤ х ≤ b, для її довжини S справедлива
формула S =
![]() .
.
-
Нехай функція ƒ невід’ємна на відрізку [a, b], де a < b та τ =
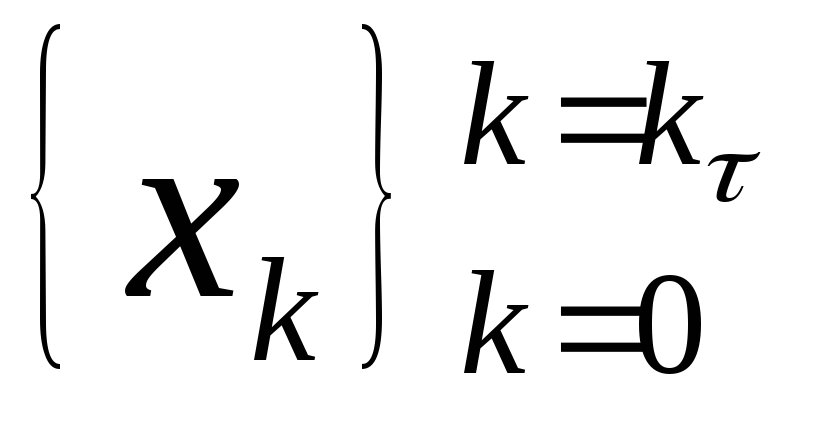 - деяке розбиття цього відрізку. Впишемо
в графік функції ƒ ламану λτ,
що відповідає розбиттю τ. Положимо Δхk
= хk
– хk-1
, Δуk
= уk
– уk-1,
тоді Δ(λτ)k
=
- деяке розбиття цього відрізку. Впишемо
в графік функції ƒ ламану λτ,
що відповідає розбиттю τ. Положимо Δхk
= хk
– хk-1
, Δуk
= уk
– уk-1,
тоді Δ(λτ)k
=
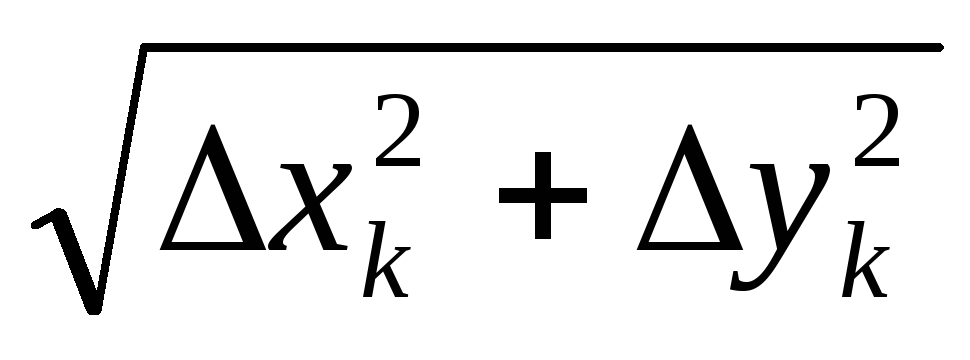 .
Тому площа поверхні обертання навколо
осі ОХ виражається формулою:
.
Тому площа поверхні обертання навколо
осі ОХ виражається формулою:
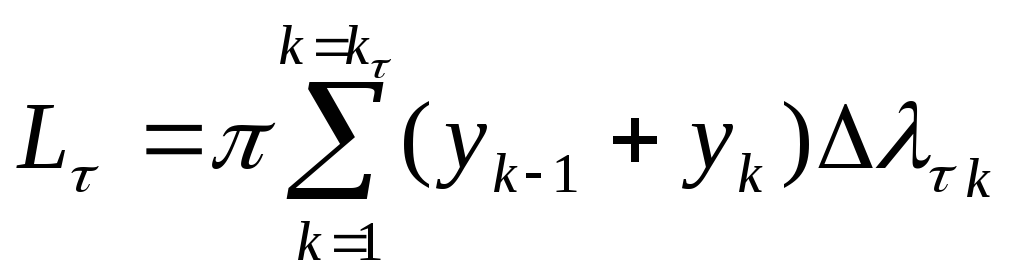 .
Якщо існує границя цієї суми
.
Якщо існує границя цієї суми
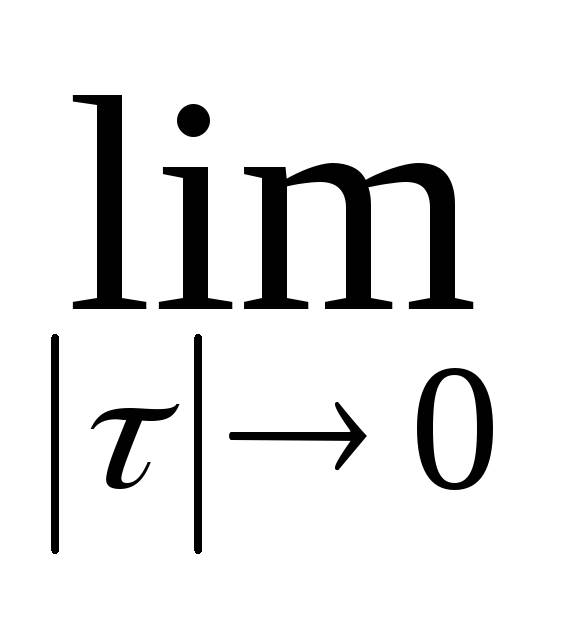 Lτ,
то вона називається площею
поверхні обертання.
Lτ,
то вона називається площею
поверхні обертання.
Для
функції у = ƒ(х) площа поверхні обертання,
що обмежена функцією у, навколо осі ОХ
має вид: L =
![]() .
.
Якщо крива задана параметрично у виді х = х(t), у = у(t) , a ≤ t ≤ b, та не перетинає ось ОХ, то площа поверхні обертання навколо осі ОХ має вид:
L
=
![]() .
.
-
Нехай функція ƒ невід’ємна та неперервна на відрізку [a, b], а Q – тіло, що отримане обертанням криволінійної трапеції Р, породженої графіком функції у = ƒ(х). Тоді об'єм V цього тіла знаходиться за формулою:
V
=
![]() .
.
Обчислення
площ плоских фігур.
Згідно
з трактовкою геометричного змісту
визначеного інтеграла, якщо функція
![]() на відрізку
на відрізку
![]() неперервна і
неперервна і
![]() ,
то площу криволінійної трапеції,
обмеженої кривою
,
то площу криволінійної трапеції,
обмеженої кривою
![]() ,
віссю
,
віссю
![]() і ординатами
і ординатами
![]() і
і
![]() (рис. 1) обчислюють за формулою (2.2).
Криволінійна трапеція
(рис. 1) обчислюють за формулою (2.2).
Криволінійна трапеція
![]() (рис. 1) в цьому випадку лежить над віссю
(рис. 1) в цьому випадку лежить над віссю
![]() .
Якщо ж
.
Якщо ж
![]() на
на
![]() ,
та фігура
,
та фігура
![]() буде лежати під віссю
буде лежати під віссю
![]() і її площа буде дорівнювати площі
рівновеликої аналогічної фігури,
обмеженої зверху кривою
і її площа буде дорівнювати площі
рівновеликої аналогічної фігури,
обмеженої зверху кривою
![]() .
Тоді згідно з формулою (2.2)
.
Тоді згідно з формулою (2.2)
|
|
(2.6) |
Об‘єднавши формули (2.5) і (2.6) в одну, одержимо
|
|
(2.7) |
Ця
формула залишається справедливою, якщо
функція
![]() на відрізку
на відрізку
![]() змінює свій знак скінчене число раз.
Дійсно, нехай
змінює свій знак скінчене число раз.
Дійсно, нехай
![]() є знакозмінна неперервна функція на
відрізку
є знакозмінна неперервна функція на
відрізку
![]()
![]() .
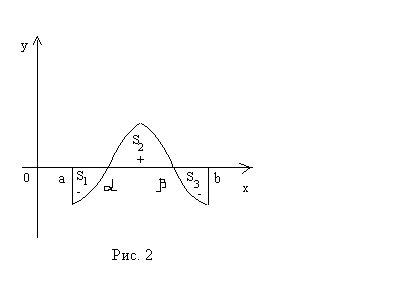
Наприклад (рис. 2),
.
Наприклад (рис. 2),
![]() при
при
![]() ,
,
![]() при
при
![]() і
і
![]() при
при
![]() .
Тоді згідно з властивістю 4 визначеного
інтеграла, та враховуючи його геометричний
зміст можна записати
.
Тоді згідно з властивістю 4 визначеного
інтеграла, та враховуючи його геометричний
зміст можна записати
|
|
(2.8) |
де
![]() - площі відповідних криволінійних
трапецій.
- площі відповідних криволінійних
трапецій.
Таким
чином, визначений інтеграл, в загальному
випадку, при
![]() є алгебраїчна сума площ відповідних
криволінійних трапецій, в якій площі
трапецій, розташованих над віссю
є алгебраїчна сума площ відповідних
криволінійних трапецій, в якій площі
трапецій, розташованих над віссю
![]() ,
беруться із знаком плюс, а площі трапецій,
розташованих під віссю
,
беруться із знаком плюс, а площі трапецій,
розташованих під віссю
![]() ,
із знаком мінус.
,
із знаком мінус.
Зауважимо, що площа заштрихованої на рис.2 фігури виражається інтегралом
![]() .
.
Очевидно,
щоб знайти площу такої фігури, потрібно
знайти нулі функції
![]() ,
тобто значення
,
тобто значення
![]() і
і
![]() ,
при яких
,
при яких
![]() і взяти суму площ цих криволінійних
трапецій.
і взяти суму площ цих криволінійних
трапецій.
Приклад.
Знайти площу фігури, обмеженої кривою
![]() прямими
прямими
![]() і
і
![]() і віссю
і віссю
![]() (рис. 3). Згідно з (2.8) та врахуванням того,
що
(рис. 3). Згідно з (2.8) та врахуванням того,
що
![]() ,
,
![]() ,
одержимо:
,
одержимо:

![]()
![]()
![]()
![]() кв.од.
кв.од.
Розглянемо
деякі інші випадки обчислення площ
криволінійних фігур. Нехай потрібно
обчислити площу фігури, обмеженої двома
неперервними лініями
![]() і
і
![]() ,
при чому
,
при чому
![]() та двома ординатами
та двома ординатами
![]() і
і
![]() (рис. 4).
(рис. 4).
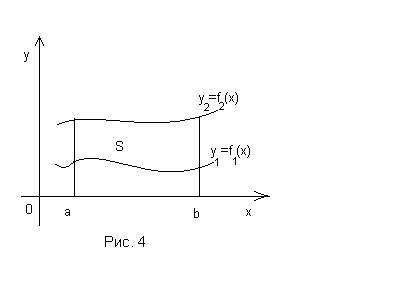
Очевидно,
що шукану площу
![]() можна розглядати як різницю площ двох
криволінійних трапецій, обмежених цими
лініями і віссю
можна розглядати як різницю площ двох
криволінійних трапецій, обмежених цими
лініями і віссю
![]() .
Отже
.
Отже
|
|
(2.9) |
Приклад.
Обчислити площу фігури, обмеженої
кривими
![]() ,
,
![]() та прямими
та прямими
![]() ,
,
![]() .
.
Згідно з (2.9)
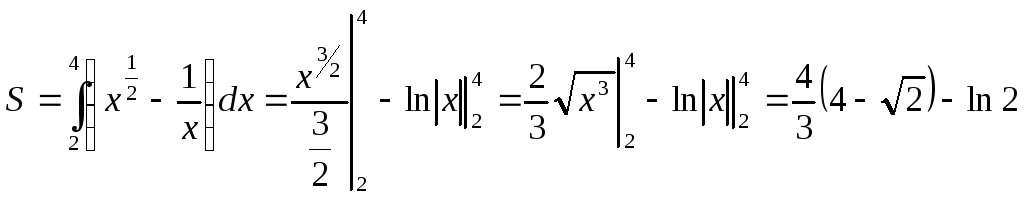 .
.
До задачі
(2.9) зводиться і задача обчислення площі
криволінійної фігури, обмеженої лініями
![]() ,
,
![]() ,
що перетинаються у двох точках. В цьому
випадку межі інтегрування визначаються
як абсциси точок перетину цих кривих і
знаходяться як розв‘язок рівняння
,
що перетинаються у двох точках. В цьому
випадку межі інтегрування визначаються
як абсциси точок перетину цих кривих і
знаходяться як розв‘язок рівняння
![]() .
.
Приклад.
Знайти площу
![]() криволінійної фігури, обмеженої кривою
криволінійної фігури, обмеженої кривою
![]() та прямою
та прямою
![]() .
.
Межі
інтегрування знайдемо із рівняння
![]()
![]()
![]()
![]() кв.од.
кв.од.
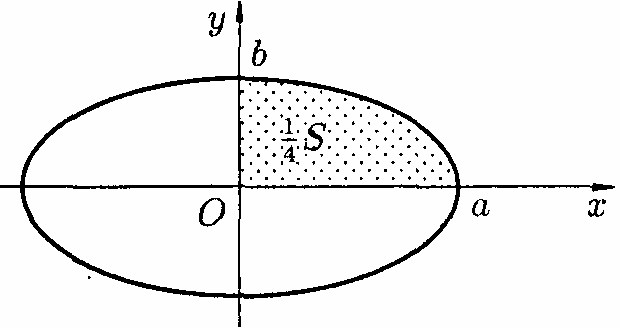
Приклад
. Обчислити
площу фігури, що обмежена еліпсом
![]() ,
,
![]() .
Знайдемо спочатку
.
Знайдемо спочатку
![]() площі S.
Тут
площі S.
Тут
![]() змінюється від 0 до
змінюється від 0 до
![]() ,
отже,
,
отже,
![]() змінюється від
змінюється від
![]() до 0.
до 0.
Знаходимо:
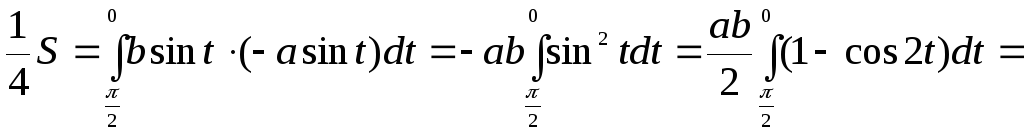 .
.
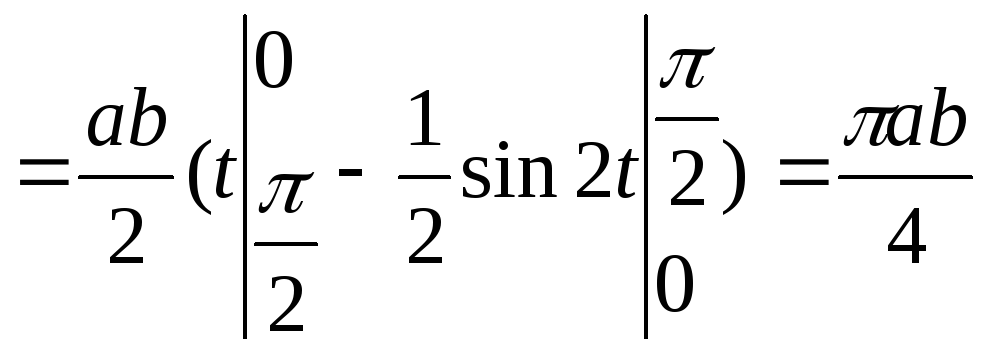
Таким
чином,
![]() .
Значить
.
Значить
![]() .●
.●
Знайдемо
площу S
криволінійного
сектора,
тобто плоскої фігури, обмеженої
неперервною лінією
![]() і двома променями
і двома променями
![]() і
і
![]() ,
де
,
де![]() і
і
![]() —
полярні координати. Для розв’язання
задачі використовуємо другу схему—метод
диференціала.
—
полярні координати. Для розв’язання
задачі використовуємо другу схему—метод
диференціала.
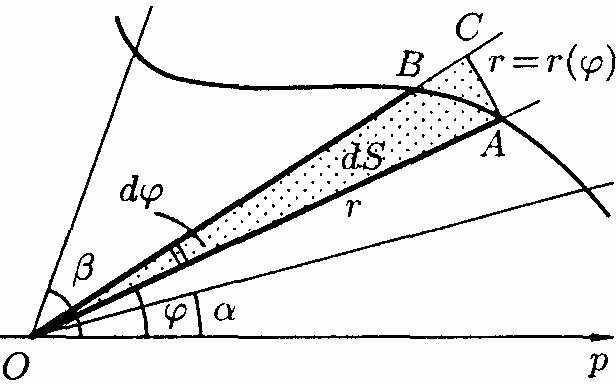
-
Вважатимемо частину шуканої площі S як функцію кута
 ,
тобто
,
тобто
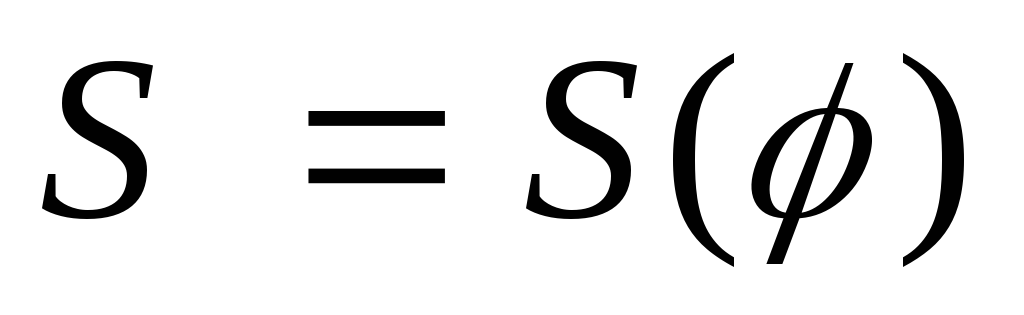 ,
де
,
де
 (якщо
(якщо
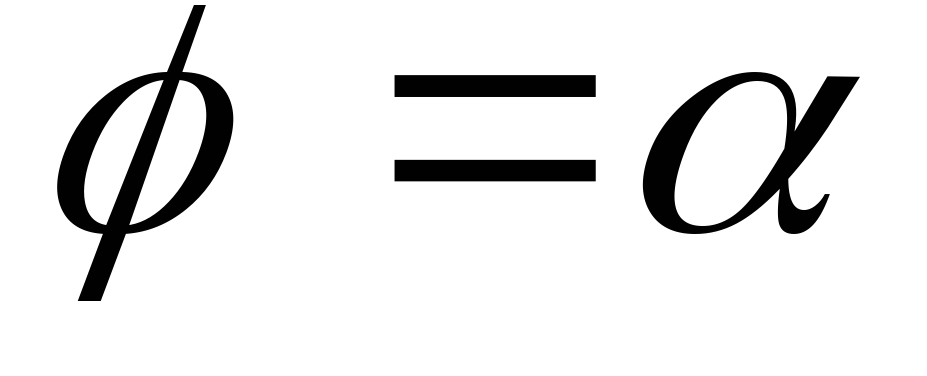 ,
то
,
то
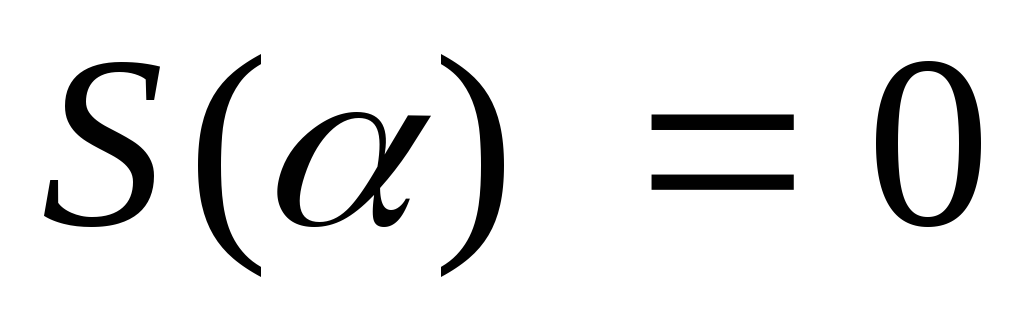 ,
якщо
,
якщо
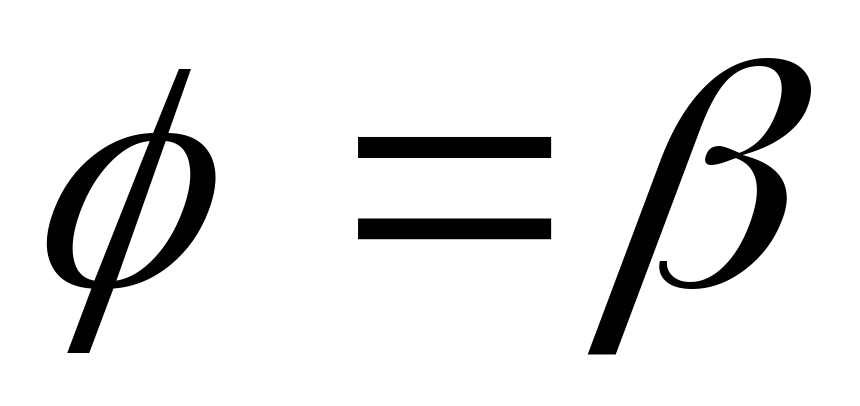 ,
то
,
то
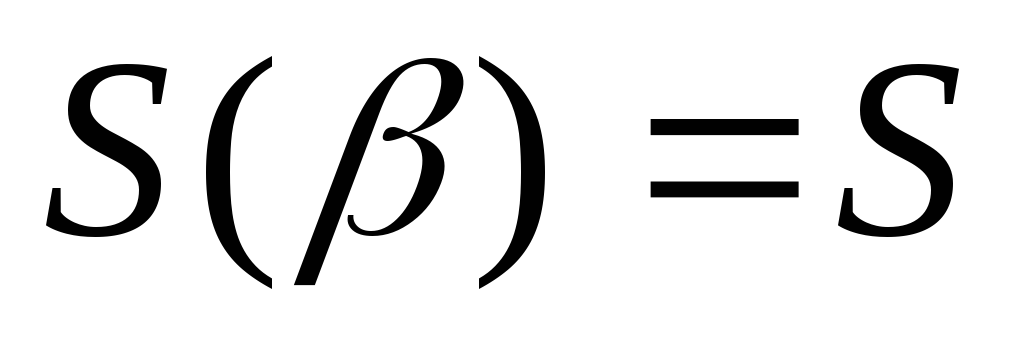 ).
). -
Якщо поточний полярний кут
 отримає приріст
отримає приріст
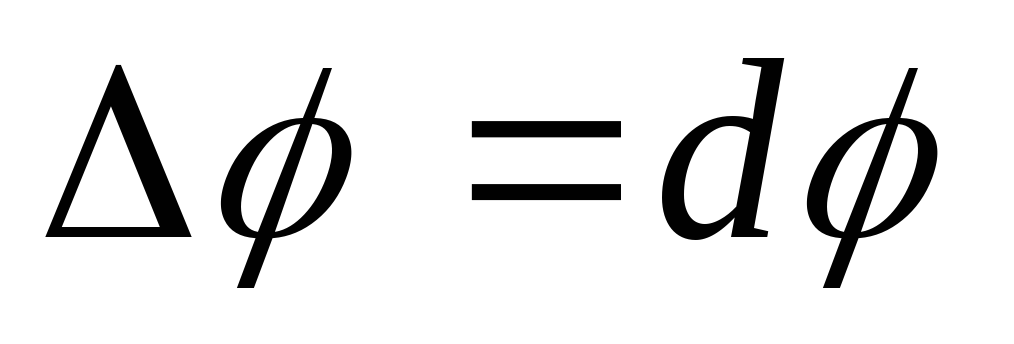 ,
то й приріст площі
,
то й приріст площі
 дорівнює площі «елементарного
криволінійного сектора»
дорівнює площі «елементарного
криволінійного сектора»
 .
.
Диференціал
![]() є головною частиною приросту
є головною частиною приросту
![]() при
при
![]() і дорівнює площі кругового сектора
і дорівнює площі кругового сектора
![]() (на рис. вона заштрихована) радіусу
(на рис. вона заштрихована) радіусу
![]() з центральним кутом
з центральним кутом
![]() .
Тому
.
Тому
![]() .
.
-
Інтегруючи отриману рівність в межах
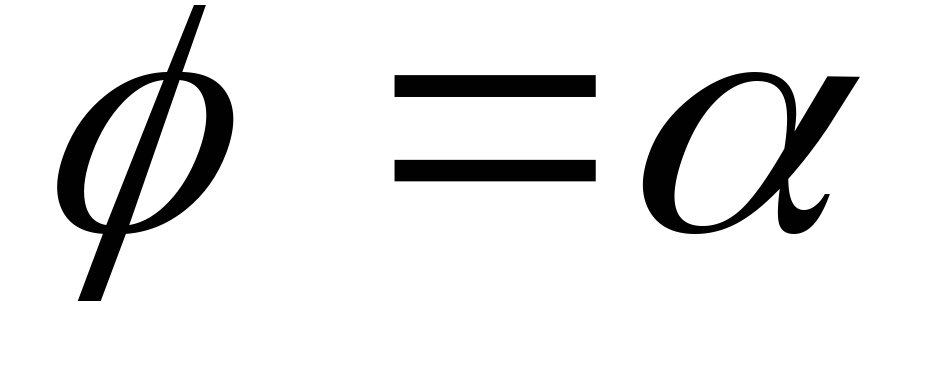 і
і
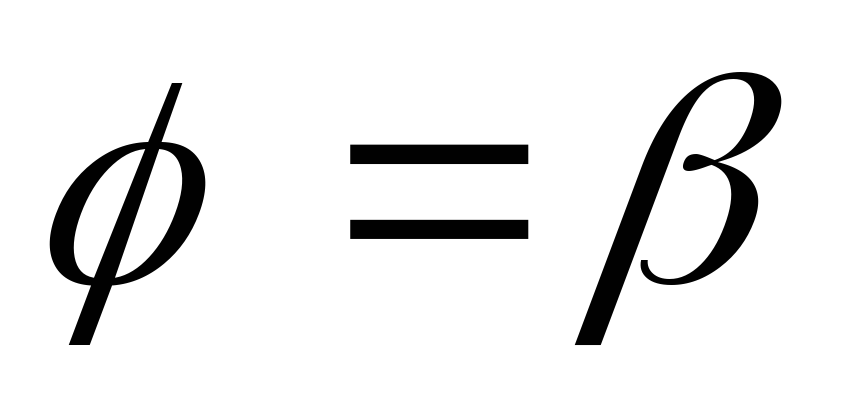 ,
отримаємо шукану площу
,
отримаємо шукану площу
![]() .
.
Приклад.
Знайти площу фігури, що обмежена
«трьохпелюстковою трояндою»
![]()
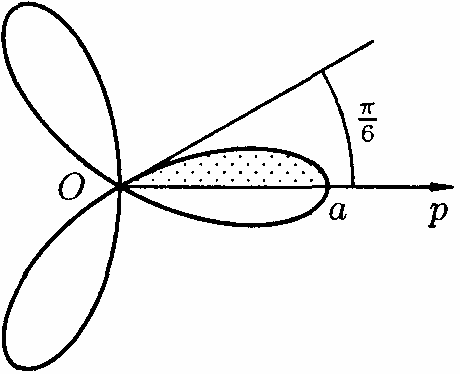
Знайдемо
спочатку площу половини одного листка
«троянди», тобто
![]() частини всієї площі фігури:
частини всієї площі фігури:
![]() ,
тобто
,
тобто
![]() .
Отже,
.
Отже,
![]() .
.
Обчислення
об‘ємів тіл. Розглянемо
задачу обчислення об‘єму
![]() тіла за відомим законом зміни площі
його поперечного перерізу
тіла за відомим законом зміни площі
його поперечного перерізу
![]() (рис. 5).
(рис. 5).
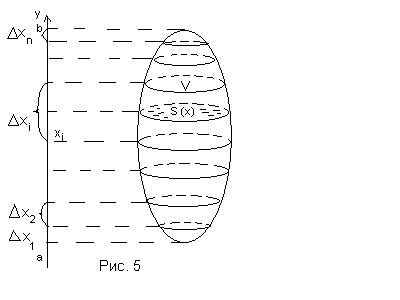
Нехай
![]() - деякий вибраний напрямок і
- деякий вибраний напрямок і
![]() - площа поперечного перерізу площиною,
перпендикулярною осі
- площа поперечного перерізу площиною,
перпендикулярною осі
![]() у
точці з абсцисою
у
точці з абсцисою
![]() .
Функцію
.
Функцію
![]() будемо вважати відомою і неперервною.
Перетнемо тіло площинами, перпендикулярними
до осі
будемо вважати відомою і неперервною.
Перетнемо тіло площинами, перпендикулярними
до осі
![]() ,
на відрізку
,
на відрізку
![]() його довжини. В результаті наше тіло
розіб‘ється на
його довжини. В результаті наше тіло
розіб‘ється на
![]() шарів, кожний з яких наближено можна
вважати за циліндр. Зважаючи на те, що
об‘єм і-го
шару наближено дорівнює
шарів, кожний з яких наближено можна
вважати за циліндр. Зважаючи на те, що
об‘єм і-го
шару наближено дорівнює
![]() ,
де
,
де
![]() - деяка точка відрізка
- деяка точка відрізка
![]() ,
то для об‘єму
,
то для об‘єму
![]() усього тіла одержимо вираз
усього тіла одержимо вираз
|
|
(2.10) |
При
![]() та
та
![]() наближена рівність (2.10) все точніше буде
характеризувати об‘єм тіла і у границі
одержимо
наближена рівність (2.10) все точніше буде
характеризувати об‘єм тіла і у границі
одержимо
![]() .
.
Оскільки
(2.10) являє собою інтегральну суму для
неперервної функції
![]() ,
то її границя є відповідний визначений
інтеграл. Отже,
,
то її границя є відповідний визначений
інтеграл. Отже,
|
|
(2.11) |
Приклад.
Знайти об‘єм
![]() піраміди, площа основи якої дорівнює
піраміди, площа основи якої дорівнює
![]() ,
а висота
,
а висота
![]() .
.
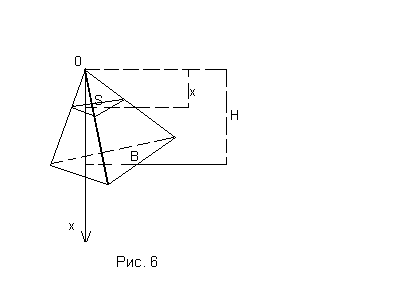
За вісь
![]() приймемо пряму, що виходить із вершини
піраміди, перпендикулярно її основі
(рис. 6).
приймемо пряму, що виходить із вершини
піраміди, перпендикулярно її основі
(рис. 6).
Позначимо
через
![]() площу якогось паралельного основі
перерізу на відстані
площу якогось паралельного основі
перерізу на відстані
![]() від вершини. Відомо, що площі паралельних
перерізів піраміди відносяться як
квадрати їх відстаней від вершини. Отже,
від вершини. Відомо, що площі паралельних
перерізів піраміди відносяться як
квадрати їх відстаней від вершини. Отже,
![]() .
Звідси
.
Звідси
![]() і на основі (2.11)
і на основі (2.11)
![]() .
.
Отриманий результат повністю узгоджується із відомою формулою геометрії.
Об‘єм
тіла обертання.
Нехай криволінійна трапеція
![]() обертається
обертається

навколо
осі
![]() (рис. 7). Оскільки площа змінного поперечного
перерізу
(рис. 7). Оскільки площа змінного поперечного
перерізу
![]() у точці
у точці
![]() є круг радіуса
є круг радіуса
![]() ,
то
,
то
![]() .
Звідси на основі (2.11) одержимо
.
Звідси на основі (2.11) одержимо
|
|
(2.12) |
Якщо ж
криволінійна трапеція обмежена графіком
неперервної функції
![]() і прямими
і прямими
![]() ;
;
![]() ;
;
![]() ,
тоді об‘єм тіла, утвореного обертанням
цієї трапеції навколо осі
,
тоді об‘єм тіла, утвореного обертанням
цієї трапеції навколо осі
![]() визначається за формулою
визначається за формулою
|
|
(2.13) |
Приклад.
Визначити об‘єм тіла, утвореного
обертанням навколо осі
![]() кола
кола
![]() .
.
Очевидно,
що обертання кола навколо осей
![]() або
або
![]() утворює кулю, об‘єм якої
утворює кулю, об‘єм якої
![]() .
Перевіримо це!
.
Перевіримо це!
Згідно з формулою (2.12) будемо мати
![]() .
.
Аналогічно,
при обертанні кола навколо осі
![]() одержимо, що
одержимо, що
![]() .
.
Обчислення довжини дуги
Означення. Під довжиною дуги розуміють границю, до якої прямує довжина ламаної лінії, вписаної в цю дугу; коли число ланок зростає, а довжина найбільшої ланки прямує до нуля.
