матан 3 курс 2013 / лекции / Функціональні послідовності і ряди / лекция № 27

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 27

з теми: «Розклад функцій в ступеневі ряди. Різні способи завдання остаточного члена формули Тейлора.»

Модуль КЗН-02.ПР.О.03.11 Функціональні послідовності і ряди

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Розклад функцій в ступеневі ряди. Різні способи завдання остаточного члена формули Тейлора.

Мета:

• Дидактична: розглянути ступеневий ряд Тейлора, навчитись знаходити розклад функцій в ряд Тейлора, радіус збіжності та коло збіжності отриманого ряду.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики проектної технології.

Тип: лекція

Вид: лекція з використанням проектної технології.

Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: визначення функціональної послідовності, визначення збіжної функціональної послідовності, визначення граничної функції, визначення рівномірно збіжної функціональної послідовності. Визначення функціонального ряду. Визначення суми ряду. Визначення збіжного та рівномірно збіжного функціонального ряду. Ознаки Вейерштраса рівномірної збіжності функціонального ряду. Ознаки Дирихлє та Абеля рівномірної збіжності функціонального ряду. Критерій Коші рівномірної збіжності функціонального ряду. Властивості рівномірно збіжних функціональних рядів і послідовностей. Визначення ступеневого ряду. Збіжність ступеневого ряду, радіус та область збіжності. Перша та друга теореми Абеля.

3. Вивчення нового матеріалу:

• Тема лекції: Розклад функцій в ступеневі ряди. Різні способи завдання остаточного члена формули Тейлора.

• Мотивація вивчення матеріалу: вивчити основні методи дослідження ступеневих рядів для подальшого їх застосування як при розв’язанні математичних, так і прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 27.

Тема: Розклад функцій в ступеневі ряди. Різні способи завдання остаточного члена формули Тейлора.

План лекції № 27.

1. Розклад функції в ступеневий ряд.

2. Різні способи запису залишкового члену формули Тейлора.

Нехай функція на відрізку або нескінчено диференційовна. Тоді для всіх значень з цього проміжку має місце формула

Такий ряд (незалежно від того, чи є він збіжним і чи має своєю сумою функцію ) називається рядом Тейлора для функції .

Поклавши в цій формулі , отримаємо ряд Маклорена:

Як і для числових рядів, суму ряду Тейлора можна представити у вигляді часткової суми ряду і -го залишку ряду: .

Для того, щоб ряд Тейлора збігався до функції , необхідно і достатньо, щоб при залишок ряду прямував до нуля:

для всіх значень із інтервалу збіжності ряду.

Теорема 1. Якщо функція ƒ розкладається в деякім околі точки в ступеневий ряд ƒ(х)= , то , n = 1, 2, …, та вірна формула ƒ(х)=.

Наслідки: Якщо в деякім околі заданої точки функція розкладається в ступеневий ряд, то такий розклад є єдиним.

Визначення 1. Нехай дійсна функція ƒ визначена в деякім околі точки та має в цій точці похідні всіх порядків. Тоді ряд називається рядом Тейлора.

Будь-яка аналітична функція в околі точки дійсної осі нескінченно раз диференційована в цій точці та розкладається в ряд Тейлора в околі точки . Зворотне твердження також є вірним: якщо функція в околі точки розкладається в ряд Тейлора, то функція є аналітичною в цій точці. Може бути так, що функція є нескінченно раз диференційована в даній точці, але не дорівнює сумі свого ряду Тейлора ні в якім околі даної точці (в даному випадку функція не є аналітичною в даній точці).

Нехай ƒ – нескінченно раз диференційована в точці функція , а її ряд Тейлора. sn(х)= - часткова сума порядку n = 1, 2, … ряду та rn(х) = ƒ(х) – sn(х) - залишковий член формули Тейлора для функції ƒ. Таким чином, ƒ(х) = sn(х) + rn(х) – формула Тейлора для функції ƒ.

Для того, щоб функція ƒ дорівнювала сумі свого ряду Тейора в деякім околі точки , потрібно, щоб в цьому околі залишковий член формули Тейлора ƒ(х) = sn(х) + rn(х) діставав до 0, коли n→∞ тобто .

Встановимо деякі види запису залишкового члену формули Тейлора.

Теорема 2. Якщо функція ƒ n+1 раз неперервно диференційована на інтервалі , то залишковий член rn(х) її формули Тейлора ƒ(х) = sn(х) + rn(х) для всіх можна записати в кожному з трьох видів:

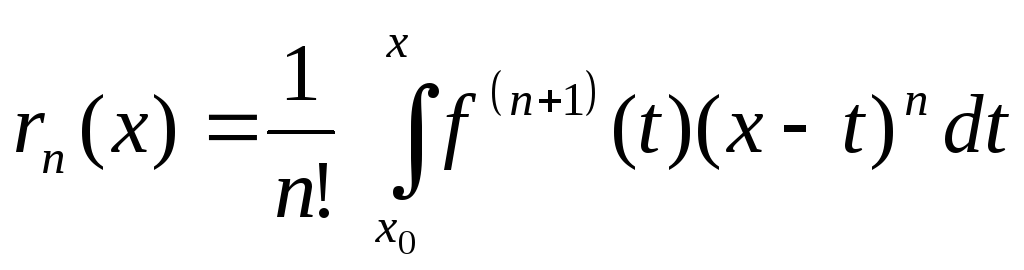- залишковий член формули Тейлора в інтегральній формі;

- залишковий член формули Тейлора в формі Лагранжа;

- залишковий член формули Тейлора в формі Коші.

Число θ, яке використовується для запису залишкового члену rn(х) залежить від х та від n.

Теорема 3 (достатня умова розкладання функції в ступеневий ряд). Якщо функція в околі точці має всі похідні, обмежені в сукупності на цім околі, то функція розкладається в ступеневий ряд в деякім околі точки .