Безкоровайний ВВ МС-конспект

z, z x.

У випадку, коли переваги не утворюють циклів, а еквівалентності не передбачаються транзитивними, кожна непуста скінченна підмножина X={x}

містить максимально кращу альтернативу xo :
xo xi x j ... xn ,	(3.6)
де xo , xi , x j , ... , xn X .

3.3Моделі задач вибору розв’язків

Умежах кардиналістичного підходу задача вибору розв’язків у багатьох випадках може бути зведена до задачі оптимізації виду (3.3). Моделі багатокритеріального оцінювання і вибору будуються на основі таких основних ФУК:

– адитивної:

m

P( x ) = ∑λi ki ( x ),

i=1

– мультиплікативної:

m λ

P( x ) = ∏[ ki ( x )] i ,

i=1

– змішаної (адитивно-мультиплікативної):

m	m
P( x ) =γ ∑	λi ki ( x ) +( 1 - γ ) ∏ [ ki ( x )]λi ,
i =1	i =1

(3.7)

(3.8)

(3.9)

де P( x ) – функція загальної корисності альтернативи x ;

γ– адаптаційний коефіцієнт, що визначає вид схеми, 0 ≤γ ≤1. При γ = 1 реалізується адитивна схема (3.7), при γ = 0 – мультиплікативна схема (3.8);

30

	m – кількість часткових критеріїв;
	λi – коефіцієнти, що характеризують								ступінь важливості критерію ki ,
i =			;
	1,m
									ki ( x ):
	ki ( x ) – нормоване значення критерію
							ki ( x ) − ki−		(3.10)
				ki ( x ) =
								,
							ki+ − ki−

де ki ( x ) – значення i-го часткового критерію для варіанта х; ki− , ki+ – найгірше й найкраще значення критерію ki .

Особливістю адитивних моделей (3.7) є необмежена можливість компенсації одних властивостей об’єкта іншими, що не завжди є припустимим. Вільними від цього недоліку є мультиплікативні моделі (3.8). Комбіновані моделі (3.9) є більш складними, проте об’єднують у собі переваги адитивних і мультиплікативних моделей.

3.4 Визначення області компромісів

Для звуження області пошуку в задачах багатокритеріального оцінювання й вибору пропонується звужувати множину (область) розв’язків X шляхом визначення множини (області) ефективних (таких, що не поліпшуються, Парето-оптимальних) розв’язків. Таку множину (область) називають множиною (областю) компромісів (ОК). Виходячи з цього множина можливих рішень Х подається у вигляді об’єднання двох підмножин X = X S X K , де X S – множина (область) згоди, будь-яке рішення з якої може бути поліпшене хоча б за одним із критеріїв без погіршення якості за іншими; X K – множина (область) компромісів, жодний із розв’язків із якої не може бути поліпшений одночасно за всіма критеріями.

Виділення ОК не є обов’язковим етапом багатокритеріальної оптимізації, але є доцільним, бо, як правило, істотно звужує область пошуку оптимального

рішення xo та не потребує перевірки оптимальності отриманого розв’язку. Точне визначення X K є досить складною задачею, що розв’язується

методами на основі теорем Карліна (для опуклих областей) і Гермейєра (для неопуклих областей). Ефективним способом її спрощення є попереднє

31

визначення наближеної області компромісів (НОК) X P . Умовами коректності процедури визначення НОК є вимога, щоб НОК містила в собі ОК: X K X P , та простота її визначення.

Суть одного з методів визначення НОК для опуклих областей Х полягає в такому. В області допустимих розв’язків Х здійснюється оптимізація послідовно за кожним із часткових критеріїв k1, k2 ,... , km . Кожен із результатів заноситься в окремий рядок таблиці (табл. 3.1). В i-му рядку таблиці подані значення всіх часткових критеріїв, що отримані при оптимізації за частковим критерієм ki. Стовпець j містить набір значень часткового критерію kj у точках оптимуму за всіма частковими критеріями. Таким чином, у кожному стовпці таблиці значення часткового критерію змінюються від найкращого k +j до

найгіршого k −j . Причому найкращі значення часткових критеріїв знаходяться

на діагоналі таблиці k +j = k jj ,

j =

.

1,m

Таблиця 3.1 – Результати оптимізації за частковими критеріями

ki \ k j

k1

k2

...

km

k1

k11

k12

...

k1m

k2

k21

k22

...

k2m

…

...

...

...

....

km

km1

km2

...

kmm

Отримана

множина пар

значень < k +j , k −j >,

j =

визначає границі

1,m

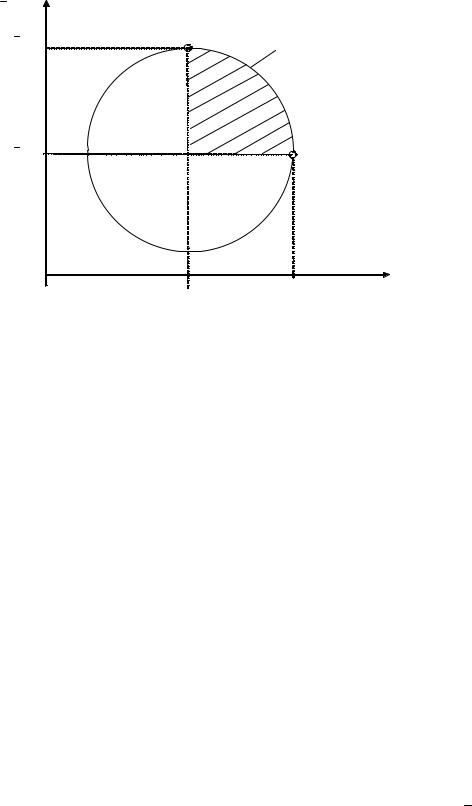
відображення НОК на простір часткових критеріїв X P → K (рис. 3.1). У загальному випадку наближена область компромісів X P містить у собі підмножину розв’язків з області згоди X S . Якщо розв’язок x XP може бути покращений за одним або декількома частковими критеріями без погіршення якості за іншими, то він не включається до X K .

Під час розв’язання дискретних багатокритеріальних задач схема визначення НОК залишається такою самою, з тією відмінністю, що матимуть місце не області, а відповідні множини розв’язків X , X P , X S , X K . У таких випадках визначення ОК може здійснюватися методом парних порівнянь. Нехай розв’язки x1 , x2, ..., xn належать X або X P . Область компромісів

32

X K складається тільки з розв’язків, що не можуть бути покращені за частковими критеріями.

k2 (x)

k22

ХK

ХР

k12

k		21	k11			k1 (x)

Рисунок 3.1 – Визначення НОК ХP на опуклій множині альтернатив Х

Алгоритм формування ОК полягає в порівнянні всіх можливих пар

розв’язків x ,x

j

XP, тобто

x

та x

2

, x

та x ,…,

x

2

та

x

, x

2

та x

4

,… і т.ін. та

i

1

1

3

3

видаленні з подальшого розгляду розв’язків, які за всіма частковими критеріями гірші за інші (інший).

3.5 Функції корисності часткових критеріїв

Ефективність розв’язків x X при багатокритеріальному підході оцінюється за множиною часткових критеріїв K = { k1 , k2 ,... , km } , де ki = fi ( x ). Часткові критерії, по-перше, можуть бути суперечливими, а по-друге, мають різний фізичний зміст, а відповідно – різні розмірність та інтервали зміни. Для вибору єдиного розв’язку з області компромісів необхідно ранжувати розв’язки за ступенем їх цінності (корисності).

У межах кардиналістичного підходу для цього використовують функції узагальненої корисності (узагальнений критерій ефективності). За наявності додаткової інформації щодо цінності властивостей альтернативи x X у моделях (3.7) – (3.9) замість нормованих значень часткових критеріїв ki ( x ) використовуються функції корисності часткових критеріїв (ФКЧК) ξi ( ki ( x )).

33

ФКЧК повинні задовольняти такі вимоги: бути монотонними і безрозмірними; мати єдиний інтервал зміни (наприклад, від 0 до 1); бути інваріантними до виду екстремуму часткового критерію (min або max); дозволяти реалізувати як лінійні, так і нелінійні залежності від значень часткового критерію.

Поняття "корисності часткового критерію" пов’язане з невизначеністю, що породжується невизначеністю поняття "найкраща система". Це робить доцільним використання для формування ФКЧК апарату теорії нечітких множин. Нехай Y = { y } – деяка множина. Нечітка (розмита) множина G на множині Y задається функцією належності ξG : Y → [ 0,1] , яка ставить у відповідність кожному елементові y Y дійсне число ξG з інтервалу [0,1] . Число ξG визначає ступінь належності нечіткій множині G . Чим ближче до 1, тим вищий ступінь належності y нечіткій множині G . Для дискретних множин Y = { y } використовується подання нечіткої множини G як множини пар елементів G = {( y, ξG ( y ))}. Тобто, частковий критерій подається як нечітка множина K j = {( k j ( x ),ξj ( x ))}.

Перерахованим вимогам відповідає, зокрема, ФКЧК виду:

k

( x ) - k

i

αi

ξ

i

(k

( x ))≡ξ

i

(x)=

i

,

(3.11)

+

i

- ki

ki

де αi – параметр, що визначає вид функції; при αi = 1 отримаємо лінійну, при 0 < αi < 1 – опуклу, при αi > 1 – увігнуту залежності від значення критерію ki ( x ) (рис. 3.2).

ФКЧК виду (3.11) може розглядатися як функція належності розв’язків розмитій (нечіткій) множині "найкращий варіант".

Поряд з ФКЧК на практиці використовуються функції втрати корисності

ξi ( x ) = 1 - ξi ( x ) .			(3.12)

Задля підвищення адекватності моделей багатофакторного оцінювання можуть використовуватися більш складні ФКЧК, що дозволяють реалізовувати лінійні, опуклі, увігнуті та S-подібні залежності від значень часткових критеріїв.

34

ξi ( x )

1

1 > αi > 0

αi = 1

αi > 1

ki−

ki+

ki ( x )

Рисунок 3.2 – ФКЧК (3.11) для ki ( x ) → mах

3.6 Формування узагальненого критерію ефективності

Інформація, що описує ситуації багатокритеріального вибору Q , на практиці може подаватися з неповною визначеністю. У таких ситуаціях використовуються моделі й методи вибору рішень в умовах невизначеності цілей, вихідних даних або ризику.

Припустимо, що ступінь невизначеності мети може бути заданий співвідношеннями значень вагових коефіцієнтів [ λi ]im=1 часткових критеріїв

[ ki ( x )]im=1 , x X (де Х – множина допустимих альтернатив; т – кількість часткових критеріїв). Найбільш характерними ситуаціями під час багатокритеріального вибору є такі: ситуація 1 – значення вагових коефіцієнтів часткових критеріїв [ λi ]im=1 невідомі; ситуація 2 – чисельні значення коефіцієнтів [ λi ]im=1 невідомі, але часткові критерії можуть бути впорядковані за ступенем важливості; ситуація 3 – відомі кількісні значення вагових коефіцієнтів [ λi ]im=1 (значення коефіцієнтів [ λi ]im=1 можуть задаватися з різним ступенем точності й вірогідності від повної визначеності до практично повної невизначеності).

У ситуації 1 природно вважати, що часткові критерії мають однакову важливість, та використовувати максимінну або мінімаксну схеми компромісу,

35

що засновані на прагненні до рівності ФКЧК:

xo = arg max min λiξi ( x ),		(3.13)
x X	i
xo = arg min max λiξi ( x ),		(3.14)
x X	i

де Х – множина допустимих розв’язків.

У ситуації 2 може бути задана система переваг часткових критеріїв, наприклад, k1 k2 … km , що дозволяє використовувати схему вибору компромісного розв’язку шляхом лексикографічної оптимізації (послідовного застосування критеріїв).

Розв’язок x лексикографічно кращий за розв’язок y , якщо виконується одна з умов:

ξ1( x ) > ξ1( y ),

ξ1( x ) = ξ1( y ), ξ2 ( x ) > ξ2 ( y ),

. . . . . . . . . . . . . . . . . . . . . . . . . .

ξi (x) =ξi ( y), i =1,m -1, ξm ( x ) > ξm ( y ) .

Суть лексикографічної оптимізації може бути подана у такому вигляді. На множині допустимих розв’язків Х необхідно знайти підмножину розв’язків X 1o X , оптимальних за найважливішим із критеріїв – k1 . На множині

розв’язків X1o знайти підмножину розв’язків X 2o , оптимальних за наступним за важливістю критерієм – k2 . На останньому етапі із підмножини розв’язків

X mo −1 знаходимо за критерієм km єдиний оптимальний розв’язок xo . При цьому

xo X mo -1 X mo -2 … X 2o X1o X K .

Якщо в процесі оптимізації за критеріями ki , i =1,m −1 буде отримано

єдиний розв’язок, відповідну множину X io , i =		розширити	шляхом
	1, m - 1
включення до неї квазіоптимальних розв’язків.
У ситуації 3 за умови незалежності часткових критеріїв ki ( x ) ,			i =
				1, m

розв’язок рекомендується вибирати з використанням універсальної адаптивної

36

моделі оцінювання, побудованої на основі адитивної схеми (3.7)

P( x ) =	1	∑m [λi			ξi ( x )]β	1 / β	,	(3.15)
m i=1
за правилом
xo = arg extr			1	∑m	[λi ξi ( x )]	β	1 / β	(3.16)
								,
x X		m i=1

де ξi ( x ) – функція корисності і-го критерію; β – адаптаційний параметр.

Змінюючи значення адаптаційного параметра в моделі (3.16), можна одержати різні схеми вибору. Так при β → ∞ виходять максимінна (3.13) та мінімаксна (3.14) схеми, що використовуються в ситуації 1, при β = 1 виходить схема, придатна для вибору рішень у ситуаціях 2 і 3:

xo = arg max ∑m	[λi ξi ( x )] ,	∑m λi = 1.
x X i=1		i=1

При β = 1 така модель дозволяє вибирати розв’язки, що максимізують сумарну корисність, при β → ∞ – розв’язки із квазірівними корисностями за

всіма частковими критеріями. За умов неможливості точного визначення (задання) значень часткових критеріїв або функцій їхньої корисності для максимального вирівнювання якості за всіма критеріями значення β може бути обране з умови:

β * = log m / log(1 +ε ),	(3.17)
де т – кількість часткових критеріїв;
ε – відносна точність визначення часткових критеріїв.
Конкретне значення адаптаційного коефіцієнта β [ 1, β*]	можна

визначити виходячи зі ступеня вірогідності визначення значень вагових коефіцієнтів [ λi ]im=1 :

37

β ′ = log m / log[1 +(m - 1)η],

(3.18)

де η – коефіцієнт ступеня визначеності мети, який визначається, виходячи з вимог до стійкості й ефективності рішень, η [ 0, 1] . Крайніми випадками є: η = 0 – повна невизначеність переваг між частковими критеріями; η = 1 – повна визначеність переваг.

Контрольні запитання та завдання

1.Сформулюйте постановку задачі прийняття рішень.

2.Назвіть основні класи задач прийняття рішень.

3.Назвіть основні підходи до розв’язання задачі ранжирування альтернатив.

4.Опишіть схему вирішення проблеми багатокритеріального вибору в межах кардиналістичного підходу.

5.Дайте визначення бінарних відношень на множині альтернатив.

6.Запишіть моделі задач вибору розв’язків.

7.Дайте визначення області компромісів.

8.Для чого здійснюється виділення області компромісів?

9.Опишіть алгоритм виділення наближеної області компромісів для опуклої області альтернатив.

10.Опишіть суть методу парних порівнянь.

11.Яким вимогам мають відповідати функції корисності часткових

критеріїв?

12.Дайте визначення нечіткої множини.

13.Наведіть формулу функції корисності часткових критеріїв.

14.Назвіть основні ситуації невизначеності мети, що виникають при прийнятті рішень.

15.Запишіть співвідношення для пошуку розв’язків за максимінним та мінімаксним критеріями.

16.Опишіть процедуру пошуку лексикографічно найкращого розв’язку.

17.Наведіть співвідношення для універсальної схеми компромісу.

18.Як визначається значення адаптаційного параметра β в

універсальній схемі компромісу?

38

4ОСНОВНІ ПІДХОДИ ДО МОДЕЛЮВАННЯ ОБ’ЄКТІВ

4.1Системний підхід до моделювання об’єктів

Під час аналізу й синтезу складних систем, до яких належить значна кількість об’єктів управління, застосовують класичний (індуктивний) або системний підходи. У межах класичного підходу об’єкт розглядається як система шляхом переходу від часткового до загального і синтезується (конструюється) шляхом злиття окремих компонентів, які розробляються роздільно. На відміну від нього системний підхід передбачає послідовний перехід від загального до часткового, коли в основі розгляду лежить мета створення об’єкта.

Фахівці з проектування й експлуатації КСУА мають справу із системами різних рівнів, які мають загальну властивість – прагнення досягти деякої мети. З урахуванням цього антропогенні системи S визначаються як цілеспрямовані множини взаємозалежних елементів будьякої природи, а зовнішнє середовище – як множина існуючих поза системою елементів будь-якої природи, що здійснюють вплив на систему або перебувають під її впливом.

При системному підході до моделювання необхідно, насамперед, чітко визначити мету моделювання. Оскільки неможливо повністю змоделювати реально функціонуючий об’єкт (систему-оригінал), відповідно до розв’язуваної задачі створюється його модель (система-модель). Стосовно моделювання мета визначається з необхідних задач дослідження, що дозволяє підійти до вибору критерію й оцінити, які елементи ввійдуть у створювану модель М. Для цього необхідно мати критерій відбору окремих елементів для створюваної моделі.

Упроцесі моделювання структура об’єкта може вивчатися ззовні з

погляду складу окремих підсистем і відношень між ними, а також зсередини, коли аналізуються окремі властивості, що дозволяють об’єкту досягати заданої мети, тобто коли вивчаються його функції. Відповідно до цього розрізнюють структурний і функціональний підходи до дослідження об’єктів.

Умежах структурного підходу виявляються склад виділених елементів об’єкта (системи S) і зв’язки між ними, тобто його структура. Остання залежно від мети дослідження може бути описана на різних рівнях деталізації. Найбільш загальним є топологічний опис структури, який

39