Задания к лабам / 3 / 03-Lit / Шифрование AES / ch2

ГЛАВА 2 Математические основы AES

AES для алгебраистов

Байты (Bytes). Бит - элемент множества F2 = Z/2Z . Восемь бит формируют один

байт. Пространство

F8

всех

байтов

определяется, как

{ f F [X ] : deg f < 8},

где

2

2

(b7b6b5b4b3b2b1b0 ) = ∑7h=0 bh X h .

Определим

отображение

λ : F28 → F28

такое,

что

λ( f ) ≡ ((X 4 + X 3 + X 2

+ X +1) f + X 6 + X 5

+ X +1) mod(X 8

+1) . Обратное ему λ−1

= λ3

выглядит, как

λ−1 ( f ) ≡ ((X 6 + X 3 + X ) f + X 2 +1) mod(X 8

+1) . Результаты всех прочих

операций для

{ f F [X ] : deg f

< 8} будем рассматривать не по модулю X 8

+1, а по мо-

2

дулю m = X 8 + X 4 + X 3 + X +1,

чтобы

F8

определялось множеством

F

= F [X ]/(m) .

2

256

2

Определим отображение

σ : F

→ F

для которогоσ(a) = λ(a254 ) ,

где a254 = a−1

для

256

256

a ≠ 0 . Длина цикла σ

соответственно 2, 27, 59, 87, и σ −1

=σ 277181 , что определяется из

σ −1 (a) = (λ−1 (a))254 .

Слова (Words). Совокупность четырех байт - слово. Преобразование из простран-

ства

F4 (= F32 ) всех слов (a

)3

к (σ(a

))3

будем также называть σ . Преобразование

256

2

i

i=0

i

i=0

ξ : F4

→ F4

определяется, как

ξ((a )3

= (σ(a

))3

(с индексами по модулю 4). Запи-

256

256

i

i=0

i+1

i=0

шем

c = (X ,1,1, X +1) и

d = (X 3 + X 2

+ X , X 3 +1, X 3 + X 2

+1, X 3 + X +1) ,

и определим

F2564

как {g F256 [Y ] : deg g < 4},

где (a0 , a1 , a2 , a3 ) = ∑i3=0 aiY i . Зададим µ,ν : F2564

→ F2564

такие µ(g) ≡ c g mod(Y 4

+1) и ν(g) ≡ d g mod(Y 4

+1) , что ν = µ−1

= µ3 .

Состояния (States). Четыре слова представляют собой состояние. Преобразование

из пространства S = (F4

)4 (= F128 ) всех состояний (w

j

)3

к (µ(w

j

))3

, к

(ν(w

j

))3

, и к

256

2

j=0

j=0

j=0

(σ(wj ))3j=0

будем соответственно называть

µ,ν,σ . Определим ρ : S → S

для которого

ρ(((ai, j )i3=0 )3j=0 ) = ((ai,i+ j )i3=0 )3j=0

(с индексами по модулю 4). Если состояние рассматривать

как матрицу 4×4, где каждый ее столбец представляет собой слово, то в этом случае ρ осуществляет циклический сдвиг каждой i -ой строки на i позиций влево (0 ≤ i ≤ 3) ; аналогично, ρ−1 = ρ3 сдвигает циклически каждую i -тую строку матрицы на i позиций вправо. Отсюда имеем ρσ =σρ. Для s S , преобразование τs : S → S определяется, как τs (x) = x + s , следовательно, τs −1 =τs и µτs =τµ(s) µ .

Разворачивание ключа (Key expansion). Ключ – пространство K равное S . Для

фиксированного		k = (wj )3j=0 K определяются индуктивные w4 , w5 ,…, w43 F2564 , где
wj = wj−1	+ wj−4	при j ≠ 0mod 4 и w j = ξ(wj−1 ) + wj−4 + (X ( j−4) / 4 ,0,0,0) при j = 0mod 4 ; а
также kl	= (w4l , w4l+1 , w4l +2 , w4l +3 ) S для 0 < l <10 .

Зашифрование и расшифрование (encryption and decryption). Сообщения разби-

ваются на блоки B по 128 бит каждый, B S . Выбирается ключ k K , и блок B зашиф-

ровыватся посредством функции εk : S → S определенной, как
εk	=τk	ρστk	µρστk	µρστk	µρστk	µρστk	µρστk	µρστk	µρστk	µρστk	µρστk	0
	10	9	8	7	6	5	4	3	8	1

17

(девять µ , десять ρ , десять σ

и одиннадцать τ представляют собой композицию слева

направо). Соответствующая функция расшифрования δk

= εk −1

представлена ниже

δ

k

=τ

ρ−1σ−1τ

νρ−1σ−1τ

νρ−1σ−1τ

νρ−1σ−1τ

νρ

−1σ−1τ

ν

k0

ν (k1 )

ν (k2 )

ν (k3 )

ν (k4 )

ν (k5 )

ρ−1σ−1τ

νρ

−1σ−1τ

νρ−1σ−1τ

νρ−1σ−1τ

νρ−1σ−1τ

k10

ν (k6 )

ν (k7 )

ν (k8 )

ν (k9 )

Словарь. Ниже приводится расшифровка терминологии используемой при обсуж-

дении элементов реализации алгоритма AES.

AddRoundKey

- одно из преобразований τkl

MixColumns

- преобразование µ определенное на S

S-box

- преобразование σ определенное на F256

ShiftRows

- преобразование ρ

SubBytes

- преобразование σ определенное на S

Раундовая константа:

- один из элементов X ( j −k ) / k

из F

, используется при

разворачивании ключа

256

Раундовый ключ

- один из элементов kl из S

Раундовое преобразование - одно из преобразований τkl µρσ ,

исключая µ при l = r (числу раундов)

Элементы теории чисел для ЭВМ

Основные группы

В математике определены: Z ={ …,−2,−1,0,1,2,…} - множество целых чисел, Z+ = {1,2,…} - множество положительных чисел, N ={ 0,1,2,…} - множество неотрицательных чисел

Целые по модулю N

Если a,b целые, и оба не равны нулю, то их наибольший общий делитель, обозначаемый, как gcd(a,b) , представляет собой наибольшее целое d делящее нацело и a и b . Если gcd(a,b) =1, то говорят, что a и b - взаимно просты. Если a,N целые, причем N > 0 , то существуют уникальные целые r, q такие, что a = Nq + r и 0 ≤ r < N . Разность

(остаток) r от деления a на N , будем называть модулем - a mod N . Отметим, что операция a mod N определена для как положительных, так и отрицательных a , и только положительных N . (В случае, кода a отрицательно, частное q также должно быть отрица-

тельным, чтобы остаток r удовлетворял условию 0 ≤ r < N .) Если a,b произвольные це-

лые и N положительное, можно говорить a ≡ b по модулю N , если a mod N = b mod N . Любому положительному N можно сопоставить следующие два множества:

ZN ={0,1,…, N −1}

Z*N ={i Z :1 ≤ i ≤ N −1 gcd(i, N ) =1}

Первое множество носит название множество целых чисел по модулю N . Размер этого множества равен N , и оно содержит исключительно целые являющиеся результатами операции a mod N при условии, что a принимает значения из Z . Определим функцию

(Euler Phi) Эйлера ϕ : Z+ → N,ϕ(N) = Z*N для всех N Z+ , тогда ϕ(N) представляет собой размер множества Z*N .

18

Группы

Пусть G непустое множество, и - бинарная операция определенная на G . Это означает, что для любых двух элементов a,b G значение a b определено. Будем назы-

вать множество G группой, если оно обладает следующими свойствами:

1. ЗАМКНУТОСТЬ: Для каждой пары элементов a,b G существует, и притом единственный, элемент c G : c = a ×b .

2.АССОЦИАТИВНОСТЬ: Для произвольных элементов a,b,c G верно равенст-

во (a b) c = a (b c) .

3.НАЛИЧИЕ НЕЙТРАЛЬНОГО (ЕДИНИЧНОГО) ЭЛЕМЕНТА (тождественность): существует такой элемент 1 G , чтоa 1 =1 a = a для всех a G .

4.НАЛИЧИЕ ОБРАТНЫХ ЭЛЕМЕНТОВ (обратимость): для любого a G суще-

ствует элемент b G , причем единственный, такой, чтоa b = b a =1 ; элемент b в этом

случае называется обратным элементу a и обозначается, как a−1 .

В любой группе можно задать операцию возведения в степень для произвольных

a G и целых i , обозначаемую, как	ai .	Результат ее определяется для i = 0 : ai =1 ,	то
есть единичному элементу группы G ,	для i >1: ai = a a … a . Если i отрицательно,		то
		i
возведение в степень определяется, как ai		= (a−1 )−i или с использованием положительно-

го показателя степени j = −i : ai = a−1 … a−1 . Используя эти определения, мы можем ма-

j

нипулировать показателями степеней, как с простыми числами. А именно, для произвольного a G и i, j Z , справедливы тождества: ai+ j = ai a j , (ai ) j = aij , a−i = (ai )−1 , a−i = (a−1 )i .

В теории групп для обозначения размера группы G используют термин порядок m . Порядок группы G есть m = G - число элементов в группе. Существует следующий факт: если любой элемент группы возвести в степень равную порядку этой группы, то результатом этой операции будет единичный элемент последней am =1, a G .

Это означает, что вычисление показателей степеней для элементов группы осуществляется по модулю m , т.е. для всех a G и всех i Z мы имеем ai = ai mod m , где m = G и операция взятия по модулю определена для всех i Z в группе.

Если G - группа, множество S G является подгруппой тогда, и только тогда, когда x y−1 S для всех x, y S , где y −1 является обратным элементом y в группе G . Для

группы G и подгруппы S группы G порядок подгруппы S делит порядок группы G . Определим следующие операции: говорят, что для любого положительного N оп-

ределена операция сложения по модулю N , которая принимает любые два целые a,b , если она возвращает в качестве результата (a +b) mod N . Операция умножения по модулю N принимает любые два целые a,b и возвращает в качестве результата ab mod N . Следо-

вательно, для положительного целого N ,	ZN - есть группа по сложению по модулю N , а
Z*N - группа по умножению по модулю N .
В ZN единичным элементом	является 0 , а обратный a элемент	есть
− a mod N = N − a . В Z*N единичный элемент - 1, обратный элемент a есть b Z*N		такой,
что ab ≡1 по модулю N .

Алгоритмы

В Таблице 2.1 перечисляются основные алгоритмы оперирующие числами. Они широко применяются в криптографии и в реализации AES, в частности.

19

При детальном рассмотрении каждого алгоритма особое внимание уделяется временным затратам требующимся на его исполнение.

Алгоритм

Параметры

Результат

Время исполнения

INT-DIV

a, N;(N > 0)

(q, r),a = Nq + r,0 ≤ r < N

O(

a

N

)

MOD

a, N;(N > 0)

a mod N

O(

a

N

)

EXT-GCD

a,b;((a,b) ≠ (0,0))

(d,

,

a

b

), d = gcd(a,b) = aa

+bb

O(

a

)

MOD-ADD

a,b, N;(a,b Z N )

(a +b) mod N

O(

N

)

MOD-MULT

a,b, N;(a,b Z N )

ab mod N

O(

N

2 )

MOD-INV

a, N;(a Z N* )

b Z N* , ab ≡1(mod N )

O(

N

2 )

MOD-EXP

a, n, N;(a Z N )

an mod N

O(

n

N

2 )

EXPG

a, n;(a G)

an G

2

n

операций над G

Таблица 2.1: Основные алгоритмы и их время исполнения. Если не указано дополни-

тельно, то входными параметрами являются целые величины, а время исполнения алгоритма определяется количеством битовых операций. G обозначает группу.

Битовые операции и двоичный (битовый) размер

В курсе алгоритмизации, рассматривается анализ времени выполнения алгоритма как функции размера входных параметров. Входные параметры обычно представляются в виде графов или массивов, и их размерность обычно выражается в количестве узлов графа или длине массива. В пределах алгоритма часто нужно выполнять простые арифметические операции, типа сложения или умножения их индексов. Обычно, стоимость одной такой операции принимается за O(1) . Причина этого предположения заключается в том, что

числа, о которых идет речь небольшие и стоимостная нагрузка на манипуляцию с ними незначительна по сравнению с издержками пропорциональными размерам массивов и графов.

Наоборот, числа, обрабатываемые в криптографических алгоритмах имеют величины прядка 2512 или 21024. Арифметические операции с такими числами - основная нагрузочная стоимость алгоритма, и издержки его производительности растут с ростом размерности этих чисел.

Возьмем bk −1 …b1b0 - двоичное представление положительного целого a , обозначе-

ние b0 …bk −1 есть биты, например, bk −1

=1 и a = 2k −1 bk −1 + 2k −2 bk −2

+…+ 21 k1 + 20 k0 . В

этом случае битовый размер a равен k ,

и называется

a

, причем

a

= k тогда, и только

тогда, когда 2k −1 ≤ a < 2k . Если a отрицательно, при допущении, что

a

=

− a

можно ис-

пользовать дополнительный бит или два для обозначения отрицательных величин.

Алгоритмы целочисленного деления и взятия по модулю N.

Определим функцию целочисленного деления принимающую в качестве входных параметров a, N , причем N > 0 , и возвращающую частное и остаток полученные в ре-

зультате деления a на N . Т.е. ее возвращаемые значения (q, r) будут удовлетворять выражению a = qN + r , где 0 ≤ r < N . Будем обозначать алгоритм реализующий такую

функцию INT-DIV. Этот алгоритм использует стандартный метод деления рассматриваемых в курсе школы, время его исполнения пропорционально двоичному размеру a, N .

Для реализации алгоритма взятия a по модулю N , принимающего целые a, N , где N > 0 необходимо осуществить вызов INT-DIV(a,N) для получения (q, r) и вернуть остаток r . Назовем функцию реализующую данный алгоритм MOD.

20

Расширенный алгоритм нахождения наибольшего общего делителя (НОД)

Полагаем a,b - целые, оба не равные 0 . Основным критерием нахождения НОД для a и b является посылка о том, что оно представляет собой наименьший положительный элемент множества {aa +bb : a,b Z} всех линейных комбинаций целых a и b . В данном случае, если d = gcd(a,b) , то существуют a,b такие, что d = aa +bb , причем как

a , так и b могут быть отрицательными .

Кроме НОД также будет полезным вычисление значений a,b , алгоритм реализую-

щий обе эти возможности называется расширенным алгоритмом нахождения НОД. Назовем функцию, реализующую этот алгоритм EXT-GCD. Входными ее параметрами будут

a,b , а результатами - (d, a,b) . Сам алгоритм является расширением классического алго-

ритма Эвклида для вычисления НОД, и самая простая его реализация осуществляется с использованием рекурсии. Алгоритм принимает любые целые a,b , оба не равные 0 .

ALGORITHN EXTGCD(a,b)

IF b = 0 THEN RETURN (a,1,0) ELSE

(q, r) ← I NTDIV(a,b)

(d, x, y) ← EXT−GCD(b, r) a ← y

b ← x −qy

RETURN (d, a,b) ENDIF

Если b = 0 предполагаем, что a ≠ 0 и gcd(a,b) = a , соответственно a = a(1) +b(0)

и	a	=1,	b	= 0 . Если	b ≠ 0 , тогда можно произвести деление для получения остатка
(q, r) ← I NTDIV(a,b)					и, далее, осуществить рекурсивный вызов функции используя тот

факт, что gcd(a,b) = gcd(b, r) . Рекурсивный вызов нам дает d = gcd(a,b) вместе со значениями x, y , поскольку d = bx + ry . При условии, что из a = bq + r , имеем:

d = bx + ry = bx +(a −bq) y = ay +b(x −qy) = aa +bb

что подтверждает корректность нахождения a,b .

Время затрачиваемое на исполнение данного алгоритма определяется, как O( ab ) или упрощенно пропорционально квадрату двоичного размера большего из a,b .

Алгоритмы сложения и умножения по модулю N

Следующие два алгоритма из Таблицы 2.1 – сложение по модулю N MODADD(a,b,N) и умножение по модулю N MODMULT(a, b, N). Чтобы вычислить

(a +b) mod N , сначала вычисляем c = a +b используя обычный школьный алгоритм, вре-

мя выполнения которого пропорционально двоичному размеру слагаемых. Можно предположить, что это при дальнейшем применении MOD(c, N) алгоритму потребуется квад-

рат времени, и это так, если бы c > N , но в большинстве случаев операция взятия по модулю может просто быть выполнена вычитанием N из c , что займет только линейное время, из чего можно сделать заключение, что в целом время исполнения алгоритма пропорционально двоичным размерам параметров. Для умножения по модулю N , процедура почти такая же. Сначала вычисляем c = ab используя обычный алгоритм, с квадратичным

21

временем, как и в предыдущем алгоритме. На этот раз вычисление MOD(c, N) необходимо осуществлять полностью, результат - O( N 2 ) .

Алгоритм вычисления мультипликативной инверсии

Рассмотрим алгоритм вычисления мультипликативной инверсии элемента a группы Z*N . На входе N > 0 и a Z N* , алгоритм MOD−INV(a, N) возвращает b удовлетворяющее выражению ab ≡1(mod N) . Приведем его реализацию:

ALGORITHM MOD−INV(a, N) (d, a, N) ← EXT−GCD(a, N)

b ← MOD(a, N)

RETURN b

Затраты на исполнение O( a N ) определяются вызываемыми алгоритмами. Убедимся в корректности алгоритма. Поскольку a Z N* известно, что gcd(a, N) =1. Вызов EXT−GCD(a, N) гарантирует, что d =1 и 1 = aa + N N . Поскольку N mod N = 0 , получаем 1 ≡ aa(mod N) , а отсюда - b = a mod N , что является верным результатом.

Алгоритм возведения в степень.

Рассмотрим алгоритм возведения в степень на групповом уровне. Имеем группу G и элемент a G . Выберем произвольное n Z , необходимо вычислить элемент группы

an рассматривавшийся в предыдущем разделе. Обычный метод вычисления выглядит: y ←1

FOR i =1,…, n DO y ← y a ENDFOR RETURN y

На первый взгляд этот алгоритм может показаться удивительно оптимальным, однако, на практике, он оказывается чрезвычайно медленным. Количество групповых операций требующееся для вычисления - n , и может оказаться большим чем порядок группы элемента a . Поскольку очень часто возникает необходимость работы с группами порядка 2512 и выше, необходим более оптимальный алгоритм.

Рассмотрим следующий реализацию:

ALGORITHM EXPG (a, n)			AND N ← −N ENFIF
IF n < 0	THEN a ← a−1
Пусть	bk −1	b1b0 - двоичное представление n
y ←1		DOWNTO 0	DO
FOR i = k −1
y ← y2 abi
ENDFOR
RETURN	y

Алгоритм работает с любыми a G и n Z . Как видно, он использует две групповых операции на итерацию: умножение y само на себя и умножение полученного резуль-

тата на abi ( причем это могут быть либо 1: bi = 0 , либо a , если bi =1). Следовательно, общая стоимость издержек составляет 2k = 2 n групповых операций (мы игнорируем стоимость возможной инверсии n при n < 0 ). Но это несколько неточное значение, актуальные затраты на исполнение данного алгоритма представляют собой n +WH (n) , где WH (n) - размер двоичного представления n в битах.

22

Вбольшинстве случаев данный алгоритм применяется в вычислениях для G Z*N

игрупповая операция является умножением по модулю N .

ВТаблице 2.1 алгоритм возведения в степень обозначается MOD-EXP и принимает

a без специального указания N , поскольку вычисления производятся в ZN . Каждая групповая операция представляет собой вызов MOD-MULT с временными затратами O( N 2 ) , в результате чего время исполнения алгоритма составляет O( n N 2 ) . Поскольку

обычно n ZN общая стоимость алгоритма MOD-EXP оценивается O( N 3 ) - кубическими временными затратами.

Алгебраические системы в реализации AES

Группы

Опираясь на материал из предыдущей главы по теории групп введем несколько дополнительных определений:

Группа G , для которой в качестве групповой операции задана операция сложения называется аддитивной, для a G нейтральным является элемент 0 , обратным (противоположным) −a .

Группа G , для которой в качестве групповой операции задана операция умножения называется мультипликативной, a G нейтральным является элемент 1, обратным

(мультипликативно) a−1 .

Группа G , групповая операция которой обладает свойством коммутативности на-

зывается коммутативной или абелевой: aib = bia ( a +b = b +a , a b = b a ).

Кольца

Кольцом R – называется множество с двумя определенными на нем операциями: первая называется сложением (обозначается + ), вторая называется умножением (обозначается ), причем имеют место следующие аксиомы:

1.Относительно сложения R является абелевой группой.

2.Замкнутость: произведение a b принадлежит R для любых a и b из R.

3.Закон ассоциативности: a(bc) = (ab)c;

4.Закон дистрибутивности: a(b +c) = ab + ac,(b +c)a = ba +ca

Сложение в кольце всегда коммутативно, а умножение не обязательно. Коммутативное кольцо – это кольцо, в котором умножение коммутативно, т.е. ab = ba для всех a и b из R.

Закон дистрибутивности в определении кольца связывает операции сложения и умножения.

Поля

Из вышеизложенного следует, что абелева группа представляет собой множество, в котором можно складывать и вычитать, а кольцо – множество, в котором можно складывать, вычитать и умножать. Более «сильной» алгебраической структурой, называемой полем, является множество, в котором можно складывать, вычитать, умножать и делить.

Полем называется множество с двумя определенными на нем операциями – сложением и умножением, причем имеют место следующие аксиомы:

1.множество образует абелеву группу по сложению;

2.поле замкнуто относительно умножения, и множество ненулевых элементов образует абелеву группу по умножению;

3.закон дистрибутивности: (a +b)c = ac +bc для любых a,b, c из поля.

23

Единичный элемент относительно сложения принято обозначать через 0 и называть нулем, аддитивный обратный элементу a элемент – через − a .

Единичный элемент относительно умножения обозначать через 1 и называть единицей, мультипликативный обратный к элементу элемент через a−1 .Под вычитанием (a −b) понимается a +(−b) ; под делением (a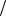b) понимается b−1a .

Известны следующие примеры полей : множество вещественных чисел, множество комплексных чисел, множество рациональных чисел.

Все указанные поля содержат бесконечное множество элементов. В криптографии интерес представляют поля, содержащие конечное число элементов. Поля с конечным числом элементов q называют полями Галуа по имени их первого исследователя Эвариста

Галуа и обозначают GF(q) .

Поля Галуа

Конечное поле задает группу двумя путями: все элементы поля образуют группу относительно умножения. На самом деле по умножению ненулевые элементы поля образуют циклическую группу. Поэтому оно порождается одним элементом. Примитивным элементом поля GF(q) называется элемент порядка (q −1) относительно умножения. Он

порождает мультипликативную группу поля.

В зависимости от значения q различают простые или расширенные поля. Поле называется простым, если q - простое число. Для обозначения простых чисел будем использовать символ p . Простое поле образует числа по модулю p : 0, 1, 2, …, p-1, а операции сложения и умножения выполняются по модулю p .

Что представляет собой наименьшее поле? Оно обязательно содержит нулевой элемент и единичный элемент, т.е. GF(2) . Правила сложения и умножения для элементов

GF(2) приведены в Таблицах 2.2 и 2.3.

+		0		1				0		1
0		0		1		0		0		0
1		1		0		1		0		1
Таблица		2.2: Правила	сложения			Таблица		2.3: Правила	умножения
	элементов в GF(2)						элементов в GF(2)

Рассмотрим возможность построения полей с элементами в виде последовательности чисел. Определим условия, при которых последовательности длины m с элементами из поля GF( p) образуют поле.

Для примера рассмотрим последовательность длины m=4 с элементами из поля GF(2) . Такие последовательности можно складывать как векторы, и нулевым элементом

по операции сложения является 0000.Для задания операции умножения сопоставим каждой последовательности многочлен от α:

	Последовательность	Многочлен
	0000	0
	0001	1
	0010	α
	0011	1+α
	0100	α2
	0001	α3
	….	….
	1111
		1+α +α2 +α3

Умножение таких многочленов может дать степень, большую чем 3, т.е. последовательность, не принадлежащую рассматриваемому множеству.

24

Например, (1101) (1001) ↔ (1+α +α3 ) (1+α3 ) =1+α +α4 +α6 . Для того, чтобы

свести ответ к многочлену степени не более 3, положим, что α удовлетворяет уравнение степени 4, например,

π(α) =1+α +α4 , или α4 =1+α

Тогда

α5 =α +α2 , α6 =α2 +α3 и 1+α +α4 +α6 =1+α +1+α +α2 +α3 =α2 +α3

Это эквивалентно делению на многочлен 1+α +α4 и нахождению остатка от деления:

α6 +α4 +α +1					α4 +α +1
+
α6	+α3 +α2
						α2 +1
α4 +α3 +α2 +α +1
+α4	+	α +1
		α2 +α3					- остаток

Таким образом, имеет место аналогия при формировании поля из чисел и последовательностей чисел или многочленов. Эта аналогия распространяется и на то, что для обратимости введенной операции умножения , чтобы система элементов в виде последовательностей длины m , образовывала поле, многочлен π(x) должен быть неприводим над

полем своих коэффициентов.

Поле, образованное многочленами над полем GF( p) по модулю неприводимого многочлена p(x) степени m , называется расширением поля степени m над GF( p) или

расширенным полем. Оно содержит pm элементов и обозначается GF( pm ) .

Поле образованное шестнадцатью двоичными последовательностями длины 4, или многочленами степени 3 и менее с коэффициентами из GF(2) по модулю многочлена

x4 + x +1, неприводимого над GF(2) , является примером расширенного поля GF(24 ) , которое может быть обозначено также GF(16) .

Важнейшим свойством конечных полей является следующее. Множество всех ненулевых элементов конечного поля образует группу по операции умножения, т.е. мультипликативную группу порядка q −1 .

Рассмотрим совокупности элементов мультипликативной группы, образованную некоторым элементом α и всеми его степенями α2 ,α3 и т.д. Так как группа конечна, то должно появиться повторение, т.е. αi =α j . Умножая это равенство на (αi )−1 = (α−1 )i , получим 1 =α j−i . Следовательно, некоторая степень α равна 1. Наименьшее положительное число e, такое, что αe =1, называется порядком элемента α. Совокупность элементов 1,α,α2 ,...,αe−1 образует подгруппу, поскольку произведение любых двух элементов

принадлежит этой совокупности, а элемент, обратный α j , равен αe− j и тоже входит в эту совокупность.

Группа, которая состоит из всех степеней одного из ее элементов, называется циклической группой.

25

Из рассмотренного свойства конечных полей вытекает два важных следствия. Первое из них утверждает, что многочлен xq−1 −1 имеет своими корнями все q −1 ненулевых элементов поля GF(q) , т.е.

xq−1 −1 = ∏(x −α)

α GF (q)

В поле GF(q) элемент α, имеющий порядок e = q −1, называется примитивным. Отсюда следует, что любой ненулевой элемент GF(q) является степенью примитивного

элемента.

Второе следствие из рассмотренного свойства утверждает, что любое конечное поле GF(q) содержит примитивный элемент, т.е. мультипликативная группа GF(q) является

циклической.

В Таблице 2.4 представлены различными способами элементы GF(24 ) . Поле GF(24 ) построено по модулю x4 + x +1. Примитивный элемент поля α является корнем

этого многочлена. Многочлен, корнем которого является примитивный элемент, называется примитивным элемент, называется примитивным многочленом. Если в качестве π(x)

выбрать примитивный неприводимый многочлен степени m над полем GF(2) , то получим поле GF(2m ) из всех 2m двоичных последовательностей длины m.

Выше было показано, что GF(4) нельзя представить в виде совокупности чисел 0, 1, 2, 3.Построим его как расширенное поле по модулю многочлена π(x) = x2 + x +1. В Таблице 2.5 элементы этого поля представлены различными способами. Здесь принято,

что примитивный элемент α является корнем π(x) , т.е. α2					+α +1 = 0 .
	В двоичном	Многочлен	Коэффициент		Степень	В десятичном
	виде		Многочлена			виде
	1	2	3		4	5
	0000	0	β0		0	0
	1000	1	β1		1	1
	0100	α	β2		α	2
	0010	α2	β3		α2	4
	0001	α3	β4		α3	8
	1100	1+α	β5		α4	3
	0110	α +α2	β6		α5	6
	0011	α2 +α3	β7		α6	12
	1101	1+α2 +α3	β8		α7	11
	1010	1+α2	β9		α8	5
	0101	α +α3	β10		α9	10
	1110	1+α +α2	β11		α10	7
	0111	α +α2 +α3	β12		α11	14
	1111	1+α +α2 +α3	β13		α12	15
	1011	1+α2 +α3	β14		α13	13
	1001	1+α3	β15		α14	9

Таблица 2.4: Варианты представления элементов GF(24 ) .

26