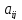- •Часть 1. Линейная алгебра и методы оптимизации 10
- •Часть 2. Теория вероятностей 79
- •1. Провести прямую через две заданные точки () и().
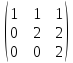
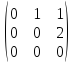
- •1. Найти сумму матриц
- •1. Предмет теории вероятностей
- •3. Статистический анализ результатов экспериментов
- •2. Для несовместных событий вероятность их суммы равна сумме
Московский государственный университет культуры и искусств
Кафедра прикладной информатики
В.С. Колосов
Математика
Учебное пособие
Москва 2011
ББК 22.1
К 61
Рекомендовано к изданию Редакционно-издательским советом МГУКИ
Рецензенты
Макаров В.Л. академик РАН д-р физ.-мат. наук,
Белоцерковский А.С. канд. техн. наук.
Колосов В.С. Математика: Учебное пособие. – М.:
МГУКИ, 2011. – 120 с.
© Московский государственный университет
культуры и искусств, 2011 © Колосов В.С.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 6
Часть 1. Линейная алгебра и методы оптимизации 10
1. Матрицы 11
1.1. Понятие матрицы 11
1.2. Арифметические операции над матрицами 12
1.3. Пример применения матриц в прогнозировании 16
2. Системы линейных уравнений
Московский государственный университет культуры и искусств 1
Кафедра прикладной информатики 1
1
ББК 22.1 2
2. Основные понятия и определения 93
4. Множество событий и операции на нем 95
Первой в списке операций логично поставить сравнение событий. Если событие В происходит всегда, когда произошло событие А, то говорят что из А следует В и обозначают символом АÌВ. 95
АВ= ВА, 97
А(ВС)=(АВ)С 97
А(В+С)=АВ+АС. 97
()= == =1. 100
6. Классическая вероятность 100
Р()= = = =1. 102
7. Схемы случайных экспериментов 103
7.1. Схема без возвращения с упорядочением 103
Величина называется числом сочетаний из n элементов по m. 105
2.1. Основные определения 17
2.2. Метод Гаусса 19
2.3. Пример моделирования экономических объектов 23
2.4. Содержательно важные аспекты анализа решений СЛУ 28
3. Векторная алгебра 30
3.1. Векторы и операции над ними 30
3.2. Векторы в системе координат 34
4. Аналитическая геометрия на плоскости 38
4.I. Способы задания линий на плоскости 38
4.2. Прямая линия на плоскости 40
4.3. Задачи о прямых 45
4.4. Взаимное расположение прямых. Геометрическая
интерпретация решения системы линейных уравнений 47
5. Методы условной оптимизации 49
5.1. Краткая история и суть вопроса 49
5.2. Постановка задачи линейного программирования 51
5.3. Дробно-линейное программирование 53
5.4. Транспортная задача 54
5.5. Математическое программирование 56
5.6. Геометрические аспекты ЛП 58
5.7. Симплекс-метод 61
Практикум 66
Матрицы 66
Системы линейных уравнений 67
Векторная алгебра 68
Аналитическая геометрия 69
Линейное программирование 72
Задачи для самостоятельного решения 76
Вопросы для самопроверки 76
Контрольные 78
Часть 2. Теория вероятностей 79
1. Предмет теории вероятностей 80
2. Основные понятия и определения 81
3. Статистический анализ результатов экспериментов 82
4. Множество событий и операции на нем 83
5. Эмпирическая вероятность 87
6. Классическая вероятность 88
7. Схемы случайных экспериментов 91
7.1. Схема без возвращения с упорядочением 91
7.2. Схема без возвращения и без упорядочения 93
7.3. Схема с возвращением и с упорядочением 94
7.4. Схема с возвращением без упорядочения 94
8. Геометрическая вероятность 96
9. Условная вероятность 100
10. Формула полной вероятности 104
11. Формула Байеса 106
Практикум 108
Операции над событиями 108
Расчет числа исходов 109
Классическая вероятность 111
Условная вероятность 113
Формулы полной вероятности и Байеса 113
Задачи для самостоятельного решения 116
Вопросы для самопроверки 117
Контрольные 118
Словарь символьных обозначений 119
Список литературы 120
ВВЕДЕНИЕ
Для многих поступающих в гуманитарный вуз заветная мечта – поскорее забыть математику как страшный сон и никогда с ней больше не встречаться. Объяснением тому служат гуманитарные наклонности и накопившееся еще в школе непонимание предмета. Однако Государственный образовательный стандарт предъявляет серьезные требования к математической подготовке будущих специалистов вне зависимости от профиля вуза,
т.к. эта наука является важной составной частью общечеловеческой культуры. Уважительное отношение к ней зародилось еще во время древней Эллады благодаря трудам Пифагора, Архимеда, Аристотеля и других ученых и инженеров. Человечество не скупилось на дифирамбы математике. В истории нашей цивилизации математика высоко ценилась не только за свои эффектные достижения в строительстве, астрономии, военном деле и других областях, но наряду с логикой она почиталась как гимнастика ума и даже возводилась в ранг «царицы наук». По мере развития математики и расширения прикладных возможностей рос и ее авторитет как науки. Так, Леонардо да Винчи утверждал, что бесспорная достоверность умозаключений в любой науке может достигаться только при использовании математических методов. Философ Р.Бэкон почти 800 лет назад выразился на этот счет куда более жестко и попросту обвинил в невежестве тех, кто не знает математику. Несмотря на излишнюю резкость, это высказывание, тем не менее, содержит изрядную долю истины. Ведь математика по существу не просто свод формул и приемов вычислений, а образец строгого логического и рационального мышления, направленного на решение совершенно конкретных задач познания окружающего мира и нашего жизнеустройства. Это подтверждают озвученные весной 2008 года результаты многолетних исследований ряда уважаемых зарубежных организаций, которые выявили тот факт, что ВВП на душу населения выше в странах с более высоким уровнем математической культуры граждан. Теперь понятно, что Дж. Буш уже располагал такой информацией, когда во время первого президентского срока призывал повысить уровень математической подготовки учащихся, хотя сам учился весьма посредственно.
В конце концов, почему знание искусства, в отличие от математики, всегда засчитывается в плюс? А ведь математика тоже искусство, причем высокое искусство интеллекта, весьма специфического рода. Вне зависимости от сферы приложения, эта наука по большому счету занимается научным обоснованием и формированием набора аналитических правил для логического заключения вида "если - тогда" и последующими числовыми расчетами на основе имеющихся исходных данных.
Математика уже давно и весьма успешно начала свое проникновение в область гуманитарных наук с немалой для них пользой. Она прочно заняла свое почетное место в управлении и бизнесе, принося прямую и немалую экономическую выгоду. В наше время убежденность в правильности принимаемого управленческого решения невозможно представить без соответствующего математического обоснования. Выпускник университета просто обязан иметь необходимую математическую подготовку.
В основе математики лежат определения и аксиомы, подсказанные интуицией, опытом и здравым смыслом. Эти базовые элементы с помощью логических рассуждений и математических построений преобразуются в целый арсенал математических методов. Созданное на таком, казалось бы зыбком, фундаменте всего лишь правдоподобных предположений и логических умозаключений здание математики, тем не менее, является грандиозным и весьма замысловатым по своей архитектуре, оставаясь в то же время стройным и изящным. Математика блестяще выдержала проверку временем. Изучая ее, испытываешь глубочайшее преклонение перед гением основоположников этой науки и их знаменитых последователей.
В настоящее время, несмотря на обилие учебной математической литературы, трудно найти один источник с рациональным сочетанием преподавания данного предмета на уровне Госстандарта и достаточного разнообразия жизненных примеров, которые убедительно показывают практическую значимость математики для широкой аудитории. В этом плане исключение составляют превосходные учебники МЭСИ (Московский государственный университет экономики, статистики и информатики). Однако они предназначены для подготовки специалистов экономико-математического и технического профиля и потому в полной мере не могут быть рекомендованы студентам МГУКИ.
В данном учебном пособии предпринята попытка компактного изложения некоторых разделов высшей математики при ограничении срока обучения этому предмету всего лишь одним семестром. В таких условиях обеспечить полное соответствие читаемого курса Госстандарту принципиально невозможно. Тем не менее, приводимые в пособии примеры практического применения математических методов призваны способствовать пониманию прикладных возможностей математики и развитию аналитического мышления с таким расчетом, чтобы с помощью приобретенных навыков будущий специалист эффективнее решал свои профессиональные задачи. Для достижения этой цели автор в меру возможности старался сделать читателей активными участниками математических построений.
Предлагаемое пособие состоит из двух частей. Первая часть под названием линейная алгебра знакомит студентов с азами таких базовых разделов математики, как "Матрицы", "Системы линейных уравнений", "Векторная алгебра", "Аналитическая геометрия", "Математическое программирование". Первые четыре раздела помимо самостоятельного значения служат элементной базой для последнего раздела, посвященного изучению оптимизационных задач планирования и принятия решений. Практическая значимость этой темы объясняется всеобщим стремлением к принятию именно оптимальных решений сообразно критериям эффективности с учетом реально существующих возможностей, Во второй части “Теория вероятностей” представлена разделом “Случайные события”. Здесь находят свое научное объяснение выражения типа “пятьдесят на пятьдесят” или “девять против одного” и решаются более сложное задачи случайного мира, в котором мы по сути дела все и живем. Опыт преподавания математики в МГУКИ последних лет убедил автора в том, что именно эта тематика обеспечивает принципиальную возможность рывка от сравнительно простых понятий до относительно сложных математических абстракций и решения практически значимых задач при достаточно глубоком понимании сути дела. Добросовестное изучение материала пособия помимо общекультурного развития неизбежно даст ценный интеллектуальный опыт освоения в малознакомой сфере деятельности, весьма полезный в нашей изменчивой жизни.
Детализация изложения содержания курса совокупно с демонстрационными примерами, вопросами для самопроверки, задачами для самостоятельного решения и контрольными примерами позволяет адресовать это пособие не только студентам дневного обучения, но и студентам вечерней и заочной форм обучения в качестве методического материала.
Ч А С Т Ь 1
Л И Н Е Й Н А Я А Л Г Е Б Р А
И М Е Т О Д Ы О П Т И М И З А Ц И И
1. Матрицы
1.1.Понятие матрицы
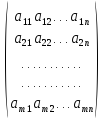
Таблица чисел (символов) из m строк и n столбцов называется прямоугольной матрицей размерности m×n, а составляющие ее элементы – элементами матрицы. В дальнейшем будут рассматриваться только числовые матрицы.
Традиционно принята следующая система символьных обозначений:
матрица – прописная латинская буква, а ее элемент – одноименная строчная буква с указанием двух индексов, означающих номера строки и столбца, в которых находится конкретный элемент. Матрицы классифицируются по внешнему признаку и внутреннему содержанию.
Сначала разберемся с внешним признаком, под которым подразумевается конфигурация матрицы как геометрической фигуры. Запись
А=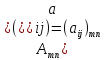 =
=
описывает
прямоугольную
матрицу A размерности m×n,
у которой на
пересечении
i-й
строки и j-го
столбца находится элемент
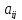 .
.
Если m=1,
то матрица состоит из одной единственной
строки
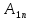 =
=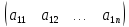 и потомуназывается
вектор-строка.
и потомуназывается
вектор-строка.
Если же n=1, то имеем вектор-столбец
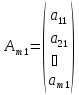 .
.
Если m=n=1,
то матрица содержит одно единственное
число
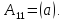 Таким образом, число является частным
случаем более общей структуры, каковой
является матрица.
Таким образом, число является частным
случаем более общей структуры, каковой
является матрица.
Особый случай представляют собой квадратные матрицы, у которых
m=n. При этом говорят уже не о размерности, а о порядке матрицы n.
В структуре
квадратной матрицы линия из левого
верхнего угла в нижний правый называется
главной
диагональю.
Элементы
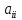 с одинаковыми индексами, находящиеся
на этой линии, называются элементами
главной диагонали.
с одинаковыми индексами, находящиеся
на этой линии, называются элементами
главной диагонали.
Среди квадратных матриц в соответствии с их содержимым выделяются следующие виды, перечисленные ниже.
Матрица, у которой либо под, либо над главной диагональю находятся только нули, называется треугольной. В приведенных ниже примерах треугольных матриц 3-го порядка символом "⋆" обозначены не нулевые элементы
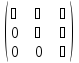 ,
,
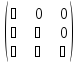 ,
, ,
, ,
,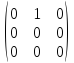 .
.
Матрица с хотя бы частично отличной от нуля одной только главной диагональю называется диагональной
 ,
,
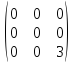 .
.
.
.
Если же диагональ заполнена одними единицами, то такая матрица называется единичной. Для нее принято специальное обозначение
Е=
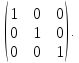
Матрица, состоящая из одних нулей, называется нулевой и обозначается
 =
=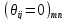 =
=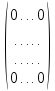 .
.
1.2. Арифметические операции над матрицами
На множестве матриц сначала определяется понятие равенства как важнейшего элемента любой математической операции, после чего вводятся арифметические операции. Умея сравнивать только два числа от равных матриц логично потребовать равенства их соответствующих элементов, т.е. находящихся в матрицах на одних и тех же местах, что автоматически влечет требование одинаковой размерности матриц. В соответствии с этим под равенством матриц понимается равенство их размерностей и всех соответствующих элементов, что с помощью введенной ранее символики может быть записано следующим образом:
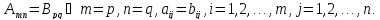
Над матрицами, как и над числами, можно производить арифмети- ческие операции сложения и умножения на число. Поскольку реально складывать мы умеем только два числа, то сложение двух совокупностей чисел, оформленных в виде матриц, разумно свести к этой парной операции, применяемой к соответствующим элементам матриц.
Сложение (вычитание) двух матриц осуществляется путем суммирования их соответствующих элементов и определяется для матриц одинаковой размерности по соображениям аналогичным равенству:
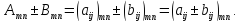
Умножение матрицы на число сводится к умножению на это число каждого элемента матрицы:
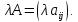
Таким образом, операции сложения матриц и умножения на число распространяются на их элементы.
Эти операции приводят к матрице с противоположным знаком
(–1)А= = –А
= –А
и нулевой матрице
0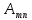 =
=
При этом нулевая матрица как и числовой 0 не меняет второе слагаемое
A+ =A, А+(–A)=А–A=
=A, А+(–A)=А–A= .
.
Из правил выполнения арифметических операций над матрицами вытекают их алгебраические свойства.
1. Сложение матриц коммутативно А+В=В+А.
2. Сложение матриц ассоциативно А+(В+С)=(А+В)+С.
3. Умножение матрицы на число ассоциативно λ(μA)= (λμ)A.
4. Умножение матрицы на число дистрибутивно относительно сложе-
ния чисел (λ+μ)A=λA+μA и матриц λ(A+B)=λA+μB.
Эти равенства слева направо читаются так скобки можно рас-
крывать, а в обратном порядке общий множитель, как число,
так и матрицу можно выносить за скобки.
5. Матрица не меняется, если ее сложить с нулевой матрицей
А+ =
= +А=А, откуда А–А=
+А=А, откуда А–А= ,
,
т.е.
 на множестве матриц играет роль,
аналогичную нулю на множестве
действительных чисел.
на множестве матриц играет роль,
аналогичную нулю на множестве
действительных чисел.
Пример суммы двух матриц с умножением второй матрицы на число:
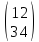
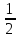
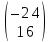 =
=
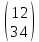 +
+ =
=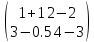 =
=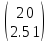 .
.
После сложения матриц и умножения матрицы на число следующим шагом является определение способа умножения двух матриц. Однако сделать это на основе каких-либо простых соображений на сей раз уже не представляется возможным. Словесное содержание алгоритма умножения матриц звучит следующим образом. Для того чтобы умножить одну матрицу на другую, надо все строки первой матрицы последовательно умножить на все столбцы второй матрицы. Умножение -й строки на 𝑗-й столбец осуществляется путем попарного перемножения их соответствующих элементов и сложения полученных результатов. При этом будет получен элемент результирующей матрицы -й строки и 𝑗-го столбца. Данное правило требует наличия соответствующих элементов в строке и столбце, а это означает, что длина строки (количество столбцов) первой матрицы должна быть равна длине столбца (количеству строк) второй матрицы.
Аналитически это правило записывается в следующем виде
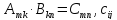 =
=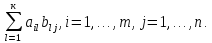
Таким образом, элемент результирующей матрицы вычисляется в виде суммы попарных произведений соответствующих элементов строки и столбца. Схематически умножение матриц можно представить так, как это сделано ниже в окаймлении рамки.
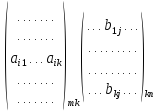 =
=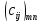
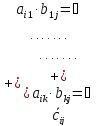
j
Пример:

Если же сомножители поменять местами, то получится совершенно другой результат матрица иная не только по содержимому, но и вообще другой размерности:
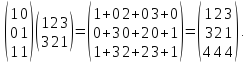
Эти примеры показывают, что результат умножения двух матриц зависит от того, в какой последовательности матрицы взяты как сомножители. Такое свойство называется некоммутативностью.
Ниже сформулированы основные свойства произведения матриц.
1. Некоммутативность АВ≠ВА.
2. λ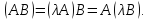
3. Ассоциативность A(BC)=(AB)С.
4. Дистрибутивность относительно сложения матриц
(А+В)С=АС+ВС,
т.е., с одной стороны можно раскрывать скобки, а с другой –
матрицу как общий множитель можно выносить за скобки.
По причине некоммутативности произведения матриц используется следующий термин: умножить матрицу А на В справа АВ или слева ВА. Таким образом, указывается та сторона матрицы А, где матрица В находится как сомножитель.
Очевидное свойство матрицы Е заключается в том, что при умножении она не меняет второй сомножитель AE=EA=A и произведение в данном случае коммутативно. Именно за это качество матрица E и названа единичной, поскольку на множестве матриц она играет роль единицы. В качестве упражнения стоит проверить, что матрица, состоящая исключительно из одних единиц, этому условию не удовлетворяет.
1.3. Пример применения матриц в прогнозировании
Известным
является факт, что при функционировании
нескольких организаций по оказанию
услуг в конкурентной среде наблюдается
переход клиентуры от одной фирмы к
другой. Для конкретизации такой ситуации
рассмотрим пример издательства.
Замечено, что в зависимости от
продолжительности подписки и меры
удовлетворенности происходит переход
подписчиков от одного издателя к
другому. Этот процесс имеет случайный
характер и может быть смоделирован
некоторой матрицей вероятностей
перехода. Безусловный практический
интерес представляет оценка ситуации
в следующем году, исходя из фактических
данных на текущий момент. Для упрощения
решения этой задачи в качестве базовой
единицы рассмотрим 1000 подписчиков,
разобьем ее на четыре категории по
продолжительности подписки:
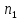 –
до 1-го года;
–
до 1-го года; – от 1-го года до 2-х лет;
– от 1-го года до 2-х лет;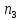 –
свыше двух лет;
–
свыше двух лет;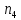 –
аннулированные подписки. Соберем эти
показатели в вектор–строку N=
–
аннулированные подписки. Соберем эти
показатели в вектор–строку N=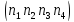 и проанализируем ее трансформацию в
следующем году, обозначив ожидаемое
распределение по тем же категориям
вектор-строкой Х=
и проанализируем ее трансформацию в
следующем году, обозначив ожидаемое
распределение по тем же категориям
вектор-строкой Х=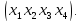 Упоминавшаяся выше матрица вероятностей
переходаP,
позволяет по численному распределению
всех подписчиков по данным категориям
в текущем году прогнозировать их
количественное перераспределение в
следующем году по формуле X=N·P. Для
условного примера примем
Упоминавшаяся выше матрица вероятностей
переходаP,
позволяет по численному распределению
всех подписчиков по данным категориям
в текущем году прогнозировать их
количественное перераспределение в
следующем году по формуле X=N·P. Для
условного примера примем
Р
=
 .
.
Если в нынешнем
году на тысячу подписчиков их
распределение по категориям определяется
строкой N=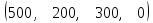 ,
то в следующем году для этой же
тысячи человек картина будет уже
такой X=
,
то в следующем году для этой же
тысячи человек картина будет уже
такой X=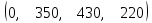 .
Содержательный анализ полученных
результатов позволяет выявить
следующие факты. Подписчики 1-й категории
в количестве 350 человек перейдут во
2-ю категорию, а 150 из них аннулируют
свою подписку, т.е. почти треть новых
подписчиков в течение первого же
года окажется полностью разочарованной
в издании. В целом полная убыль
клиентуры по всем категориям составит
220 человек, что превышает 20%. Такая
информация дает серьезный повод для
размышлений и поиска решений с целью
изменения ситуации к лучшему. К числу
таких мер относится изменение формата
издания, интервенция рекламы и т.п.
Характер рассмотренного примера
позволяет рассчитывать на правомерность
такого подхода при решении аналогичных
задач в сфере оказания услуг, в
частности для компаний мобильной
связи.
.
Содержательный анализ полученных
результатов позволяет выявить
следующие факты. Подписчики 1-й категории
в количестве 350 человек перейдут во
2-ю категорию, а 150 из них аннулируют
свою подписку, т.е. почти треть новых
подписчиков в течение первого же
года окажется полностью разочарованной
в издании. В целом полная убыль
клиентуры по всем категориям составит
220 человек, что превышает 20%. Такая
информация дает серьезный повод для
размышлений и поиска решений с целью
изменения ситуации к лучшему. К числу
таких мер относится изменение формата
издания, интервенция рекламы и т.п.
Характер рассмотренного примера
позволяет рассчитывать на правомерность
такого подхода при решении аналогичных
задач в сфере оказания услуг, в
частности для компаний мобильной
связи.
2. Системы линейных уравнений
2.1.Основные определения
Системой линейных алгебраических уравнений из m уравнений с n переменными называется система вида
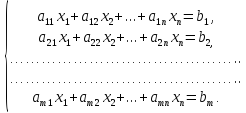
Здесь величины
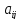 называются
коэффициентами системы, а числа
называются
коэффициентами системы, а числа – свободными членами. Решением системы
линейных уравнений называются значения
неизвестных
– свободными членами. Решением системы
линейных уравнений называются значения
неизвестных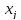 ,j=1,…,n,
удовлетворяющие одновременно всем
уравнениям системы.
,j=1,…,n,
удовлетворяющие одновременно всем
уравнениям системы.
Введенное ранее правило умножения матриц позволяет представить данную систему в компактной матричной форме АХ=В, где А матрица
коэффициентов системы, а В и Х – вектор-столбцы свободных членов
и неизвестных соответственно:
A
=
 ,B
=
,B
=
 =
=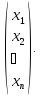
Матрица коэффициентов системы и вектор-столбец свободных членов объединяются в так называемую расширенную матрицу, разделенную на две соответствующие секции вертикальной линией, символизирующей знак равенства
 =
=
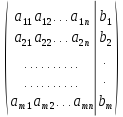 =
= .
.
Расширенная матрица содержит все числовые параметры системы и тем самым описывает ее самым исчерпывающим образом. По этой причине в дальнейшем система линейных уравнений будет отождествляться именно с расширенной матрицей.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не существует ни одного решения. Совместная система называется определенной, если ее решение единственно, и неопределенной, если решение не единственно.
2.2. Метод Гаусса
Этот метод органично предопределяется своим объектом, т.е. системой линейных уравнений. Для лучшего понимания сути дела сначала рассмотрим простую систему двух уравнений с двумя неизвестными
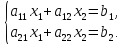 Ее расширенная
матрица
Ее расширенная
матрица
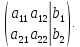
Решить такую систему – значит найти значения неизвестных, удовлетворяющие сразу всем уравнениям, т.е. свести ее к виду
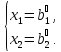
Последние два равенства, очевидно, также являются системой линейных
уравнений, каждое из которых содержит лишь одну неизвестную. Дополнив каждое из них другой переменной, взятой с нулевым коэффициентом, получим следующую систему линейных уравнений
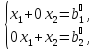 с расширенной
матрицей
с расширенной
матрицей
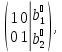
левая секция которой представляет собой единичную матрицу Е.
Таким образом, если правильно перейти от матрицы А к Е, то на месте столбца свободных членов в правой секции расширенной матрицы окажется решение задачи. Остается только определить, с помощью каких операций такой переход можно осуществить. Ответить на этот вопрос позволяет содержательный анализ изучаемого объекта. Самым простым действием, не меняющим решение задачи, является перестановка местами уравнений системы. Далее, имея дело с равенством, можно умножить обе его части на одно и то же число. Наконец, к обеим частям равенства можно прибавить одну и ту же величину. Однако к равенству мы будем прибавлять не число, а другое равенство, умноженное на некоторое число, осуществляя сложение почленно, складывая, соответственно левые и правые части. При этом произойдет сложение соответствующих коэффициентов при переменных. Например, прибавление ко второму уравнению первого равенства, умноженного на λ, даст следующий результат
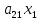 +
+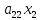 +λ
+λ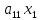 +λ
+λ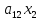 =
=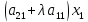 +
+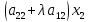 =
= +
+ .
.
Таким образом, арифметические операции реально производятся исключительно над числовыми параметрами системы, а сами переменные играют роль общих множителей. При этом величину λ целесообразно выбрать с таким расчетом, чтобы коэффициент при одной из переменных обратился в нуль, что фактически будет означать исключение соответствующей неизвестной. Осуществлению всех перечисленных действий над уравнениями системы соответствует выполнение аналогичных операций над строками расширенной матрицы и наоборот. Сформулируем теперь свод правил преобразований расширенной матрицы, которые принципиально не могут испортить решение системы линейных уравнений, если оно конечно существует. Введем следующие символические обозначения:
i
⃝
⇄
к ⃝
— переставить местами две строки с
указанными номерами;
i
⃝
λ — умножить i-ю
строку на число λ;
i
⃝
+ к
⃝
λ — к i-й
строке прибавить к-ю
строку, умноженную на λ. 
Второе действие обеспечивает получение единиц путем деления на подходящую величину. Последнее действие при сложении двух строк использует предыдущую операцию и обеспечивает обнуление элементов матрицы коэффициентов. Все три действия в совокупности образуют группу элементарных преобразований (ЭП) матриц и составляют алгоритмическую основу метода Гаусса. При этом следует помнить, что, оперируя со строками расширенной матрицы, мы те же самые действия производим над уравнениями системы и каждому столбцу матрицы коэффициентов соответствует определенная переменная. В результате приведения матрицы коэффициентов к единичной матрице происходит обнуление коэффициентов при переменных, что означает их фактическое исключение из соответствующих уравнений. Поэтому метод Гаусса называют еще методом исключения неизвестных. Заметим, что во всех построениях не было необходимости в каких-либо ограничениях на размерность системы уравнений. Продемонстрируем применение метода Гаусса на численных примерах.
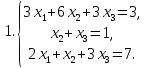
Составим расширенную матрицу данной системы линейных уравнений и найдем ее решение методом исключения неизвестных. Для обеспечения регулярности действий в программных реализациях алгоритма Гаусса сначала обнуляется часть матрицы А под главной диагональю (нижний левый угол) и так называемый “прямой ход” завершается преобразованием матрицы коэффициентов в верхнюю треугольную. Затем обнуляется верхний правый угол матрицы А и “обратный ход” заканчивается
построением единичной матрицы. При решении задач будем руководствоваться именно этим принципом. Итак, приступим:
 .
.
Распаковав
полученную матрицу, найдем решение
 =2
и, подставив эти величины в уравнения
системы, нетрудно удостовериться в
правильности полученного решения.
=2
и, подставив эти величины в уравнения
системы, нетрудно удостовериться в
правильности полученного решения.
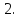

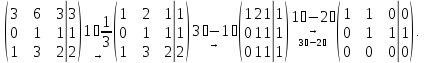
Трансформация последней матрицы в систему линейных уравнений дает следующий результат:
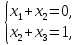
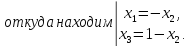
Отсюда следует,
что придавая
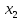 произвольные значения, найдем
соответствующие им величины
произвольные значения, найдем
соответствующие им величины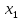 и
и и в результате получим бесконечное
множество решений. Таким образом,
признаком неединственности решения
системы линейных уравнений является
образование нулевой строки в
расширенной матрице в процессе
элементарных преобразований.
и в результате получим бесконечное
множество решений. Таким образом,
признаком неединственности решения
системы линейных уравнений является
образование нулевой строки в
расширенной матрице в процессе
элементарных преобразований.
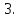
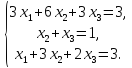
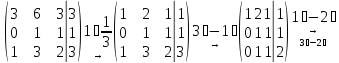

На сей раз в расширенной матрице появилась строка, которую можно истолковать как противоречие "0=1". Однако это противоречие мнимое, и сигнализирует оно о несовместности системы. В самом деле, принципиальной особенностью элементарных преобразований является сохранение равенств. В случае несовместности не существует значений переменных, которые одновременно удовлетворяли бы всем уравнениям системы. Вследствие этого, хотя бы одно из уравнений не может выполняться как точное равенство, и вместо знака равенства имеет место неравенство. Сложение равенства с неравенством даст конечно же неравенство, чем и объясняется непротиворечивость такой строки.
Метод Гаусса реализован во всех пакетах математических программ. Его эффективность заключается в том, что он легко справляется не только со случаем единственного решения, но и выявляет ситуации не единственности решения и его отсутствия вообще.
В соответствии
с изображенной ниже принципиальной
схемой метода Гаусса, как только на
месте матрицы коэффициентов А
в результате элементарных
преобразований матрицы
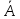 окажется единичная матрицаЕ,
тогда место вектор-столбца свободных
членов займет искомое решение задачи
X:
окажется единичная матрицаЕ,
тогда место вектор-столбца свободных
членов займет искомое решение задачи
X:
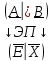
Если же в расширенной матрице образуется полностью нулевая строка, то это означает неединственность решения. Отсутствию решения будет соответствовать нулевая строка в левой секции и ненулевая величина справа.
Вычислительная схема метода Гаусса построена здесь без использования формул исключительно на основе действий, не нарушающих равенства.
2.3. Пример моделирования экономических объектов
Системы линейных уравнений находят широкое применение при решении практических задач в различных областях. Эффективное использование матричного исчисления в моделировании экономики США нашим соотечественником В.В. Леонтьевым, положило начало работе по созданию экономических механизмов защиты от кризисных ситуаций за счет рационального сочетания государственного регулирования и свободного рынка. Как показало время, эта работа дала неплохие результаты, и призрак великой депрессии 30-х годов не грозил бы миру, если бы идеи и наработки многих ученых экономистов и математиков не были преданы забвению. Учитывая предостережения аналитиков еще за два года до обвала в ипотечном секторе США, положившим начало всеобщему кризису, бездействие международных финансовых институтов и правительств вызывает глубокое недоумение. И только после того как грянул гром все дружно зашевелились.
В конце войны, Леонтьев в результате глубокого и всестороннего анализа экономики США предсказал, что после победы спрос на металл не только не упадет, чего все опасались, а наоборот возрастет за счет строительного бума и оказался совершенно прав.
Впечатляющий пример научной и практической деятельности Леонтьева дает послевоенный период, когда он с коллективом ученых и специалистов был приглашен в Японию. Леонтьев один из общепризнанных идеологов японского экономического чуда. Располагая достоверной экономической информацией этого островного государства, он создал всеобъемлющую модель межотраслевого баланса, которая послужила весьма эффективным руководством к действию. Серьезное отношение правительства Японии к эконометрическим идеям и практическим наработкам Леонтьева и других ученых и специалистов в планировании и прогнозировании способствовало выдвижению страны Восходящего Солнца на лидирующие позиции в мире. В знак признания заслуг ученого-практика Япония приняла на себя хлопоты по сохранению его научного наследия, выкупив у США его личную библиотеку и создав на этой основе музей. Всемирное признание идей и практического вклада Леонтьева сделали его почетным членом множества университетов в различных странах мира, лауреатом Нобелевской премии по экономике за 1973 г., кавалером высших наград, к числу которых относятся орден Почетного Легиона, орден Восходящего Солнца и т.д.
В период становления РФ как самостоятельного государства и коренной перестройки всей экономики Леонтьев получил соответствующее предложение Б. Ельцина и охотно принял его. Однако, несмотря на искреннее желание ученого применить свои знания с пользой для родины, он был вынужден от этого отказаться в силу противодействия со стороны олигархических кругов, которые не были заинтересованы в наведении строгого учета хозяйственной деятельности. По этому поводу можно выразить только глубокое сожаление, поскольку профессиональная некомпетентность реформаторов, а также алчность и нечистоплотность бизнеса вызвали лихорадочные метания нерегулируемого псевдо рынка, дефолт и непомерную инфляцию, которые тяжким бременем легли на плечи нашего многострадального народа. В то же время развитые страны восточной Европы продемонстрировали возможность куда менее болезненного перехода на другую политическую, экономическую и хозяйственную платформу.
В дальнейшем периодически будет употребляться термин "математическая модель" или просто "модель". Математической моделью объекта называется система математических соотношений, описывающих количественные и качественные зависимости его элементов знаками математической символики. Эконометрические идеи Леонтьева нашли свое воплощение в моделях межотраслевого баланса, суть которых можно продемонстрировать на простом примере.
Рассмотрим функционирование n отраслей экономики в течение определенного промежутка времени. Каждая отрасль производит свою продукцию (товары и услуги), которая является частично конечным продуктом внепроизводственного (общественного потребления), а частично идет на удовлетворение собственных внутриотраслевых нужд (продукты обмена).

Конечное потребление

Другие отрасли
Так сталелитейная промышленность выпускает сталь, из которой изготавливаются рельсы и крепежные изделия (болты, гайки и т.п.). И то и другое потребляют сама сталелитейная промышленность, а также машиностроение, строительство, железнодорожный транспорт, обеспечивая перевозку людей и грузов, в том числе крепежа и рельсов для себя и других отраслей, сырья для сталелитейных заводов, крепежа как конечного продукта и т.д. Ввиду большой сложности всеобъемлющей модели ограничимся изучением, так называемой однопродуктовой модели (каждая отрасль производит только один продукт).
Обозначим:
n количество рассматриваемых отраслей;
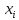 объем продукции
произведенной i-й
отраслью;
объем продукции
произведенной i-й
отраслью;
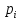 объем конечного
продукта потребления i-й
отрасли;
объем конечного
продукта потребления i-й
отрасли;
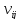 объем продукции
i-й
отрасли, использованный j-й
отраслью.
объем продукции
i-й
отрасли, использованный j-й
отраслью.
Моделью межотраслевого баланса Леонтьева называется система равенств, обеспечивающая строгую сбалансированность объемов производства с внутриотраслевым и конечным потреблением. Если в модель включены все отрасли, использующие все продукты обмена, то она называется консервативной. В рамках консервативной модели объем всей произведенной продукции идет на удовлетворение потребностей в конечном продукте и обеспечение нужд других отраслей в этом продукте, т.е. нет ни дефицита, ни перепроизводства:
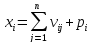 ,
i=1,
. . . ,n.
,
i=1,
. . . ,n.
Обозначим
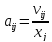 .
Эти величины называют коэффициентами
прямых затрат, поскольку они определяют
количество единиц продукцииi-й
отрасли, необходимое для изготовления
единицы продукции j-й
отрасли.
.
Эти величины называют коэффициентами
прямых затрат, поскольку они определяют
количество единиц продукцииi-й
отрасли, необходимое для изготовления
единицы продукции j-й
отрасли.
Тогда
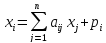 ,
i=1,
. . . ,n
,
i=1,
. . . ,n
или в компактной матричной записи
X=AX+P,
где Х=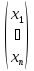 и Р=
и Р=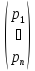 вектор-столбцы объемов производства
и конечного
вектор-столбцы объемов производства
и конечного
потребления, а
квадратная матрица A=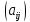 характеризует потребности
характеризует потребности
отраслей друг в друге и называется матрицей прямых затрат.
Решением данной системы уравнений является совокупность значений неизвестных Х (план задачи), обеспечивающая удовлетворение потребностей в конечном продукте в размере Р с учетом внутриотраслевого потребления, определяемого матрицей А. В соответствии с правилами матричных операций, перепишем полученную систему в виде
EX=AX+Р или (EA)X=P.
Однако экономическое
содержание задачи требует дополнительно
еще и неотрицательности решения
(плана), что будет выполнено не для любой
матрицы А с неотрицательными
элементами. В случае существования
решения задачи при любых объемах
конечного потребления матрица А
называется продуктивной. Продуктивность
матрицы А будет обеспечена, если
для всех ее столбцов сумма их элементов
не превосходит единицы, а хотя бы для
одного столбца (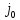 )
это неравенство является строгим, т.е.
)
это неравенство является строгим, т.е.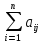 ≤1,j=1,
. .
≤1,j=1,
. .
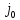 1,
1,
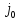 +1,
. . .n,
+1,
. . .n,
 <1
(критерий продуктивности).
<1
(критерий продуктивности).
Пример. Экономическая система состоит из двух объектов с заданной матрицей прямых затрат и объемов потребления в условных единицах.
|
|
1 2 |
P |
|
1 2 |
0,2 0.4 0,6 0.1 |
160 90 |
Согласно приведенному критерию, матрица прямых затрат продуктивна, и поэтому решение задачи существует. Вычисляем расширенную матрицу (ЕАР) и с помощью метода Гаусса находим план задачи:

 ,
,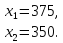
Таким образом, для обеспечения сбалансированного функционирования
двух отраслей им надлежит произвести продукцию в указанных объемах.
2.4. Содержательно важные аспекты анализа решений СЛУ
При анализе систем линейных уравнений в прикладных задачах ситуации совместности и несовместности, единственности и неединственности решения могут играть как положительную, так и отрицательную роль. Характеристика этих ситуаций в категориях "хорошая" или "плохая" определяется существом объекта или процесса, отображаемого системой линейных уравнений. Если система уравнений моделирует условия банкротства компании, то существование решения означает ее неминуемый крах, что, конечно же, нежелательно. В то же время отсутствие решения в данной ситуации является безусловным благом. Если система уравнений описывает деятельность строительной организации, то существование единственного решения может означать, например, что сдача объекта в срок возможна лишь в случае неукоснительного соблюдения графика необходимых работ. Таким образом, существование единственного решения в зависимости от конкретной ситуации в содержательном отношении может быть как достоинством, так и недостатком.
Полезную информацию содержит также случай образования нулевых строк в матрице коэффициентов системы в процессе ее преобразований по методу Гаусса. Такая ситуация свидетельствует о наличии в системе уравнений, которые как бы дублируют некоторую часть уравнений системы. Содержательный анализ системы на предмет самостоятельной роли ее уравнений способствует выявлению несущественных факторов, что представляется весьма полезным.
Ситуация с неединственным решением является наиболее интересной и перспективной. В этом случае разумно поставить задачу выбора из множества решений такого, которое было бы наилучшим в смысле некоторого критерия, к примеру, минимума затрат, максимума дохода, минимизации сроков строительства, минимизации отходов при раскрое материалов и т.п. Именно с неединственности решения начинается тернистый путь к задачам оптимизации, играющим чрезвычайно важную роль в различных сферах человеческой деятельности, а уж о менеджменте и говорить не приходится. Это ничуть не удивительно, поскольку формулировка оптимизационной задачи в самом общем виде звучит следующим образом: из множества равнозначных решений, допускаемых системной условий задачи, выбрать наилучшее из них в соответствии с некоторым критерием оптимальности. Практическая значимость оптимизации объясняется тем, что под такую формулировку подпадает подавляющее большинство задач принятия решения, и в том числе задач планирования и управления. Даже в своей повседневной жизни мы стремимся находить именно оптимальные решения. Взять хотя бы приобретение бытовой техники. Например, при покупке холодильника кто-то будет руководствоваться соображениями минимальной стоимости при выполнении определенных условий: высота, количество камер, наличие антибактериального покрытия, количество компрессоров или термостатов, уровень шума и т.п. В противоположность этому другой покупатель, не заботясь о цене, будет стремиться приобрести холодильник производителя с наиболее высоким рейтингом, опять-таки предъявляя определенные требования к устройству и дизайну товара. При этом в нашем сознании высокий рейтинг фирмы производителя связывается с высоким качеством товара и как следствие с его более высокой ценой.
Строгая математическая формализация простой оптимизационной задачи будет изучена позже. Однако уже сейчас из рассмотренных соображений совершенно ясно, что ее обязательными атрибутами должны быть критерий оптимальности, как выразитель эффективности принимаемого решения и система условий, в которой учтены ограничения реально существующих возможностей.
3. Векторная алгебра
3.1. Векторы и операции над ними
Сами того не замечая, мы постоянно сталкиваемся с величинами, которые характеризуются не только своими значениями, но и направлением: движение тела, приложение усилия и т.п. Такие величины называются векторами и являются объектами изучения "Векторной алгебры". В наших целях достаточно ограничиться рассмотрением двухмерного случая, т.е. плоскости, которая допускает простую геометрическую интерпретацию векторов и операций над ними.
Вектором называется упорядоченная пара точек, первая из которых является его началом, а вторая – концом. Понятие точки как объекта с нулевыми линейными размерами предполагается изначальным и интуитивно ясным. В соответствии с данным определением у вектора имеется две характеристики его направление и длина, как расстояние между его начальной и конечной точками. Начала векторов (точки их приложения) могут быть выбраны произвольно, и потому векторы называются свободными. Это означает, что возможен параллельный перенос свободного вектора в любую другую начальную точку с сохранением его направления и длины.
Из этого определения следует, что векторы в отличие от отрезков или прямых линий не могут пересекаться принципиально, будучи внутри “пустыми”. В этом смысле для обеспечения корректности школьное определение вектора как направленного отрезка, соединяющего две точки, требует следующего пояснения. Отрезок здесь фигурирует исключительно как категория длины, и это вовсе не означает, что вектор вместе со своими начальной и конечной точками содержит все внутренние точки отрезка их соединяющего.
Принята следующая система обозначения и изображения векторов:
 A и B
соответственно начальная и концевая
точки вектора
A и B
соответственно начальная и концевая
точки вектора
 ,
стрелка указывает его направление.
Расстояние между началом и концом
вектора (длина отрезка [A,
B])
называется его длиной (модулем) и
обозначается 𝑎=
,
стрелка указывает его направление.
Расстояние между началом и концом
вектора (длина отрезка [A,
B])
называется его длиной (модулем) и
обозначается 𝑎= =
=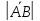 =AB.
Если начало вектора совпадает с его
концом, то вектор нулевой
=AB.
Если начало вектора совпадает с его
концом, то вектор нулевой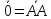 .
.
Для векторов вводятся понятия (см. словарь символьных обозначений):
коллинеарности – векторы одинаково или противоположно направлены;
сонаправлености – векторы коллинеарные и имеют одно направление;
антинаправлености – коллинеарные и противоположно направленные;
ортогональности – угол между векторами равен 90°.
Теперь есть все необходимое для определения операций над векторами. Сначала, конечно же, следует установить условия равенства векторов. У вектора две характеристики направление и длина. Отличие соответствующих характеристик двух равных векторов было бы, разумеется, противоестественным.
Векторы
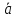 и
и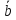 называют равными, т.е.
называют равными, т.е.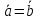 ,
если они сонаправленные и имеют
одинаковую длину
,
если они сонаправленные и имеют
одинаковую длину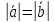 или в
символической
записи
или в
символической
записи
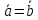 ⇔
⇔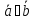 и
и
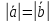 .
.
Определяя над векторами операции сложения и умножения, следует указать, по какому алгоритму в этих операциях характеристики векторов преобразуются в результат операции.
В качестве
первой операции рассмотрим сложение
векторов. Однако для прояснения
ситуации сначала сложим два числа
геометрически, а конкретно 2 и 3. Для
этого на числовой оси отложим сначала
2 единицы, а затем еще 3. Рассматривая
эту операцию как сумму двух коллинеарных
векторов длиной соответственно 2 и
3 единицы, получим вектор длиной 5.
При этом начало второго вектора
оказалось помещенным в конец первого,
а суммарный вектор прошел из начала
первого вектора в конец второго.
Понятное дело, что правило сложения
векторов произвольного направления
не может противоречить алгоритму
сложения коллинеарных векторов. В
этом рассуждении заложен ключ к
обоснованию алгоритма сложения двух
векторов в общем случае. 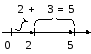
Суммой двух
векторов называется вектор, идущий
из начала первого вектора в конец
второго, при условии, что начало
второго вектора совмещено с концом
первого
вектора.
Сложение
векторов в силу геометрии данной
операции
называется правилом треугольника.
При этом однозначно определяется
направление и длина вектора, являющегося
суммой двух векторов, а сама операция
осуществляется, следуя логике
геометрического сложения чисел.
Далее вводится операция умножения вектора на число. Поскольку параметрами вектора являются его направление и длина, то следует определить, что с ними произойдет в результате умножения на число. Множитель может быть как положительным, так и отрицательным. Длина вектора величина безусловно положительная и потому на нее может повлиять только модуль множителя. На долю знака множителя логично отнести изменение направления вектора на противоположное.
Умножить
вектор
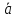 на число λ означает: построить вектор
λ
на число λ означает: построить вектор
λ длиной
длиной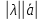 с направлением вектора
с направлением вектора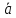 при положительном λ и противоположного
направления при отрицательном λ . В
соответствии с принятой системой
обозначений правило умножения вектора
на число в символьном виде можно
записать так:
при положительном λ и противоположного
направления при отрицательном λ . В
соответствии с принятой системой
обозначений правило умножения вектора
на число в символьном виде можно
записать так:
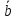 =λ
=λ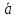 ⇔
⇔
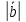 =
=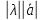 и
и
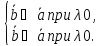
Таким образом, умножение вектора на число способ изменения его длины с возможным изменением направления на противоположное. Отсюда следует, что признаком коллинеарности ненулевых векторов является их отличие друг от друга лишь на числовой множитель, т.е.
 ‖
‖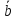 ⟺
⟺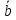 =λ
=λ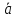 при некотором λ.
при некотором λ.
Если задаться
целью, перемножив два вектора получить
число, то разумно перемножить их
длины и дополнительно к этому учесть
их направления. Для двух векторов
на плоскости вводится понятие
скалярного
произведения
посредством формулы: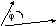
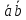 =
=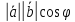 ,
,
где
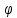
угол между векторами
угол между векторами
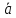 и
и
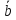 .
.
В этой формуле учитываются не абсолютные направления векторов, а их расположение относительно друг друга.
Из определения
следует, что скалярное произведение
двух векторов равно нулю тогда и
только тогда, когда либо векторы
ортогональны (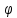 =90°),
либо один из них равен нулю, т.е.
=90°),
либо один из них равен нулю, т.е.
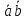 =0
⟺
=0
⟺
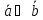 (
(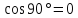 )
либо
)
либо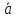 =0
или
=0
или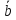 =0
(коротко
=0
(коротко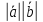 =0).
=0).
Таким образом, признаком ортогональности векторов является равенство нулю их скалярного произведения.
Свойства операций над векторами
1. Достроив
треугольник до параллелограмма, как
это показано на рисунке, и производя
сложение по его противоположным
сторонам (сплошная и пунктирная линии),
нетрудно убедиться, что
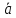 +
+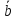 =
=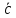 =
=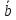 +
+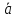 .Независимость
суммы векторов
от порядка слагаемых называется
коммутативностью.
.Независимость
суммы векторов
от порядка слагаемых называется
коммутативностью.
2. Непосредственным построением проверяется ассоциативность
сложения векторов (скобки определяют приоритет операции)
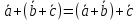 .
.
3. Вектор не меняется, если его сложить с нулевым вектором
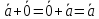 .
.
4. Вектор
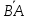 называется противоположным вектору
называется противоположным вектору и обо-
и обо-
значается
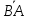 =
= =
=  .
При этом
.
При этом
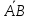 +
+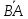 =
=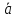
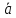 =
=
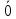 .
.
5. Умножение вектора на число ассоциативно относительно умно-
жения
чисел
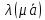 =
=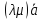 .
.
6. Умножение вектора на число дистрибутивно относительно
сложения
чисел
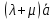 =λ
=λ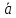 +μ
+μ и векторов
λ
и векторов
λ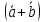 =λ
=λ +λ
+λ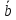 .
.
Эти равенства означают, что скобки можно раскрывать, а общий
множитель, как число, так и вектор можно выносить за скобки.
7. Скалярное
произведение коммутативно
 =
=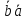 ,
поскольку
,
поскольку
в силу
четности косинуса
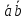 =
=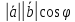 =
=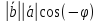 =
=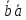 .
.
8. Для любых
λ,
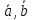 справедливо равенство
справедливо равенство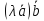 =
= =
=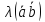 .
.
9. Скалярное произведение дистрибутивно относительно сложения
векторов
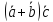 =
=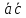 +
+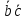 .
Это равенство означает возможность
.
Это равенство означает возможность
раскрытия скобок и вынесения общего множителя за скобки.
10. Скалярный
квадрат вектора ( =1)
дает
=1)
дает =
=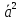 =
=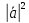 .
.
3.2. Векторы в системе координат
Пусть
даны два ненулевые и не коллинеарные
векторы
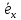 и
и ,
тогда любой вектор
,
тогда любой вектор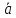 может быть представлен в виде
может быть представлен в виде
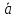 =
=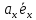 +
+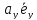
и это представление
единственно. В
самом деле, если
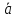 ‖
‖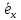 (
(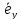 ),
то по свойству коллинеарных векторов
они отличаются друг от друга только на
числовой множитель
),
то по свойству коллинеарных векторов
они отличаются друг от друга только на
числовой множитель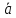 =λ
=λ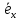 (
(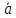 =λ
=λ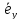 ).
Отсюда находим λ=
).
Отсюда находим λ=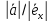 (λ=
(λ= )
в случае сoнаправлености векторов и
λ=
)
в случае сoнаправлености векторов и
λ=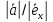 (λ=
(λ=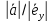 ),
если векторы антинаправлены. Теперь,
полагая
),
если векторы антинаправлены. Теперь,
полагая
 =λ,
=λ, =0
(
=0
(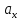 =0,
=0,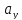 =λ)
получаем требуемый результат.
=λ)
получаем требуемый результат.
В случае
неколлинеарности
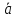 векторам
векторам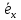 и
и на этих векторах как
на этих векторах как
на сторонах
строится параллелограмм с таким
расчетом, чтобы вектор
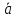 являлся его диагональю. По построению
вектор
являлся его диагональю. По построению
вектор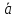 представляется в виде суммы
представляется в виде суммы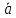 =
=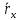 +
+ ,
где
,
где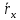 ‖
‖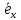 и
и
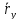 ‖
‖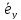 .
По свойству коллинеарных векторов
они отличаются только на числовой
.
По свойству коллинеарных векторов
они отличаются только на числовой
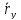

множитель и тогда
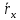 =λ
=λ
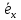 ,
,
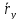 =μ
=μ
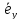 .
Теперь полагая
.
Теперь полагая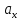 =λ,
=λ,
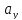 =μ
получим
=μ
получим
 =
=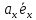 +
+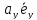 .
.
Говорят, что два
ненулевые и неколлинеарные векторы
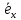 и
и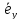 на плоскости
образуют
базис. Запись
вектора
на плоскости
образуют
базис. Запись
вектора
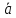 в виде линейной комбинации
базисных
векторов называется его разложением
по базису или представлением в
базисе
в виде линейной комбинации
базисных
векторов называется его разложением
по базису или представлением в
базисе
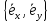 ,
а числа
,
а числа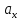 и
и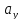 называются координатами вектора
называются координатами вектора в этом базисе.
в этом базисе.
Дополнение
базиса некоторой точкой "0",
принимаемой за начало отсчета, дает
систему координат.
Наиболее распространенной является
хорошо знакомая еще со школы, декартова
система координат с взаимно
перпендикулярными осями и единичным
ортогональным базисом
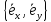 ,
т.е.
,
т.е.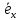 ⊥
⊥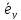 ,
,
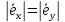 =1.
Названа она так в честь своего творца
– французского математика Рене Декарта
(ХVII
век).
=1.
Названа она так в честь своего творца
– французского математика Рене Декарта
(ХVII
век).
В этой системе
координат вектор
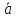 =
=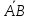 ,
идущий из точкиA
,
идущий из точкиA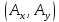 в точку В
в точку В по правилу треугольника может быть
представлен в виде суммы
по правилу треугольника может быть
представлен в виде суммы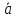 =
=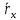 +
+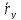 =
=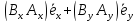 ,
поскольку по построению
,
поскольку по построению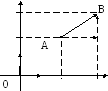
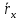 ‖
‖ ,
,
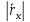 =
=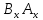 ⇒
⇒
 =
= ,
,
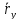 ‖
‖ ,
,
 =
=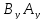 ⇒
⇒
 =
=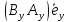
или в координатной
форме
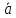 =
=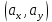 ,
где
,
где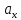 =
= ,
,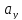 =
=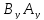 .
.
Cами
базисные векторы своими координатами
будут иметь
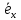 =(1,0),
=(1,0),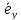 =(0,1).
=(0,1).
Таким образом, координаты вектора его проекции на оси координат, и их вычисление сводится к вычитанию из координат концевой точки соответствующих координат начальной точки. Ориентация вектора в системе координат определяется численными значениями его координат, которые в свою очередь характеризуют взаимное расположение начальной и конечной точек. Координаты вектора определяют координаты его концевой точки относительно произвольно выбранной начальной точки. В самом деле, поскольку вектор свободный, то в качестве его начальной точки может быть выбрана любая точка плоскости. Координаты концевой точки вычисляются сдвигом из начальной точки на соответствующие величины вдоль осей координат в направлениях, определяемых знаками координат вектора:
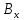 =
=
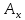 +
+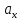 ,
,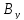 =
=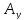 +
+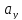 .
.
Свойства векторов в декартовой системе координат конкретизируются следующим образом.
1. У
равных векторов соответствующие
координаты равны:
 =
= ,
,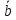 =
=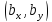 ,
,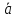 =
=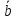 ⟺
⟺
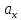 =
=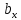 ,
,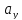 =
=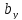 .
.
2. При суммировании векторов складываются их соответствующие координаты. Используя свойство дистрибутивности, находим
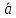 +
+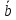 =
=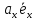 +
+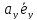 +
+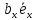 +
+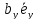 =
=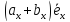 +
+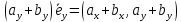 .
.
3. При умножении вектора на число на это число умножаются его координаты
λ =λ
=λ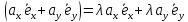 =
=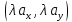 .
.
4. Ненулевые векторы – коллинеарные тогда и только тогда, когда имеет место пропорциональность их соответствующих координат:
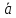 ‖
‖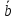 ⟺
⟺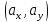 =
=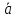 =λ
=λ =λ
=λ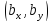 =
=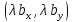 ⟺
⟺
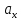 =
=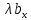 ,
, =
=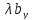 .
.
Выразив из двух последних равенств параметр λ, получим пропорцию
λ
=
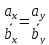 .
.
При λ=1
из пропорции находим
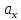 =
=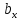 и,
и,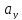 =
=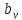 ,
что и подтверждает равенство координат
равных векторов.
,
что и подтверждает равенство координат
равных векторов.
5. В декартовой системе координат скалярное произведение равно сумме попарных произведений соответствующих координат, а длина вектора вычисляется по теореме Пифагора (очевидно из рисунка):
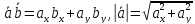 .
.
В самом деле, в
силу того, что
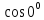 =1
и
=1
и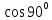 =0
имеем
=0
имеем
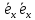 =
=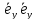 =1,
=1,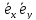 =
=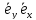 =0.
=0.
Раскрывая скобки в соответствии со свойством дистрибутивности, найдем
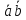 =
=
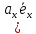 +
+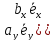 +
+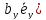 =
=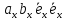 +
+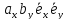 +
+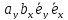 +
+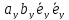 ,
,
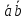 =
=
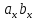 +
+ ,
,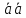 =
=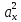 +
+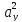 ,
,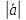 =
=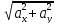 ,
, =
=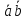 /
/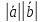 .
.
Основным
назначением скалярного произведения
является вычисление угла между
векторами и, в частности, выявление
ортогональности векторов.
Примеры.
Дано: А(3,5), В(4,6),
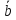 =(2,1).
=(2,1).
Найти и построить
векторы
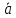 =
=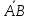 ,
,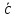 =
=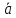 2
2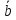 .
.
Проверить
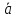 ‖
‖
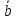 ,
,
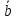 ,
найтиφ
угол
,
найтиφ
угол
между векторами
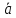 и
и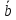 .
.
Решение.
1.
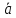 =
=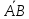 =(43,
65)=(1,1).
=(43,
65)=(1,1).
2.
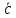 =
=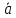 2
2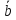 =(1,1)+(4,2)=(14,
1+2)=(3,3).
=(1,1)+(4,2)=(14,
1+2)=(3,3).
При графическом
изображении этой операции вектор
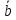 может быть построен изначально в
любой точке плоскости, в частностиc
начальной
может быть построен изначально в
любой точке плоскости, в частностиc
начальной
точкой в начале
координат, как это показано на
рисунке. Поскольку вектор свободный,
то путем параллельного переноса
совместим его начало с концом вектора
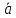 .
Удлинив вектор
.
Удлинив вектор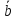 вдвое и изменив его направление на
противоположное, построим вектор2
вдвое и изменив его направление на
противоположное, построим вектор2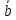 .
С тем же успехом вектор2
.
С тем же успехом вектор2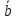 =(–4,2)
можно было построить сразу исходящим
из конца вектора
=(–4,2)
можно было построить сразу исходящим
из конца вектора
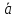 со сдвигом концевой точки относительно
начальной точки на 4 единицы влево
по оси абсцисс и на 2 деления вверх
по оси ординат в соответствии со
знаками и величинами координат этого
вектора.
со сдвигом концевой точки относительно
начальной точки на 4 единицы влево
по оси абсцисс и на 2 деления вверх
по оси ординат в соответствии со
знаками и величинами координат этого
вектора.
Коллинеарность
векторов
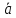 и
и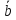 проверяется пропорциональностью их
соответствующих координат:
проверяется пропорциональностью их
соответствующих координат:
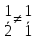 ⇒
⇒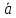 ∦
∦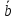 .
.
Признаком ортогональности векторов является равенство нулю их скалярного произведения:
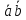 =1211=1
=1211=1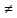 0⇒
0⇒
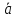 ∤
∤
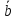 .
.
4. Аналитическая геометрия на плоскости
4.I. Линии на плоскости и способы их задания
Под системой
координат подразумевается метод
численного описания местоположения
точки на плоскости парой чисел. Как
и ранее, будем рассматривать декартову
систему координат. Для произвольной
точки плоскости А(х,у)
ее радиус-вектором называется вектор
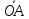 =(x,y),
где х
– абсцисса точки, а у
– ее ордината. Числа x и y однозначно
определяют положение точки на плоскости,
т.е. каждой точке плоскости соответствует
единственная пара чисел, и наоборот.
Иными словами, система координат
отождествляет пару чисел и точку на
плоскости с соответствующими
координатами.
=(x,y),
где х
– абсцисса точки, а у
– ее ордината. Числа x и y однозначно
определяют положение точки на плоскости,
т.е. каждой точке плоскости соответствует
единственная пара чисел, и наоборот.
Иными словами, система координат
отождествляет пару чисел и точку на
плоскости с соответствующими
координатами.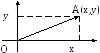
Существует два способа задания линии – геометрический и ана- литический. В соответствии с первым способом линия на плоскости задается как множество точек, обладающих определенным геометрическим свойством, т.е. формулируется основное геометрическое свойство линии. Аналитический способ заключается в задании линии уравнением f(x,y)=0, связывающим координаты точек линии между собой. Графиком линии G называется множество точек плоскости, координаты которых и только они удовлетворяют уравнению линии G={(x,y) : f(x,y)=0}. Переменные x и y в уравнении линии называются текущими координатами произвольной точки линии М(x,y).
Примеры
1. Биссектриса второго и четвертого квадрантов G={(x,y) : x+y=0}. Эта
запись описывает линию, сумма координат точек которой равна нулю.
Координаты точек этой линии равны по абсолютной величине и противоположны по знаку y= x.
2. Проверить, лежат ли на линии x+y+2=0 точки А(1,1) и В(1,1). Подстановкой убеждаемся, что точка А принадлежит линии, а точка В – нет.
Факт
пересечения двух линий
 (x,y)=0
и
(x,y)=0
и
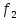 (x,y)=0
выявляется по наличию общих точек,
координаты которых удовлетворяют
обоим уравнениям, т.е. являются решением
соответствующей системы уравнений.
Если таковых нет, то линии не
пересекаются.
(x,y)=0
выявляется по наличию общих точек,
координаты которых удовлетворяют
обоим уравнениям, т.е. являются решением
соответствующей системы уравнений.
Если таковых нет, то линии не
пересекаются.
Аналитическая геометрия решает две задачи:
- по заданным геометрическим свойствам линии составить ее уравнение;
- по заданному уравнению выяснить геометрические свойства линии.
При этом
геометрический способ предопределяет
правило построения уравнения линии.
В качестве примера найдем уравнение
окружности радиуса r
с
центром в начале координат. Окружность
определяется как геометрическое место
точек, равноудаленных от центра
(основное геометрическое свойство).
Данное определение конструктивно,
поскольку, взяв на окружности
произвольную точку М(x,y)
и применив теорему Пифагора к
прямоугольному треугольнику с катетами
x
,
y
и гипотенузой r,
получим уравнение
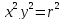 или
или +
+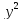
 =0,
которое и является уравнением
окружности радиуса r
с центром
в начале координат.
=0,
которое и является уравнением
окружности радиуса r
с центром
в начале координат. 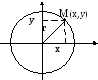
Пусть теперь в качестве исходных данных имеется уравнение
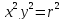 ,
где r
некоторое
число. Отождествляя переменные x
и
y
с координатами точки на плоскости
и рассматривая это уравнение как
формулу Пифагора, справедливую для
произвольной точки линии, в качестве
ее геометрического свойства получаем
равноудаленность точек линии от
начала координат, т.е. основное свойство
окружности с центром в начале
координат.
,
где r
некоторое
число. Отождествляя переменные x
и
y
с координатами точки на плоскости
и рассматривая это уравнение как
формулу Пифагора, справедливую для
произвольной точки линии, в качестве
ее геометрического свойства получаем
равноудаленность точек линии от
начала координат, т.е. основное свойство
окружности с центром в начале
координат.
4.2. Прямая линия на плоскости
Прямая
определяется как линия, расстояния
между двумя любыми точками которой
является кратчайшим.
К сожалению, это определение не
конструктивно в том смысле, что в
отличие от геометрического свойства
окружности основное геометрическое
свойство прямой не позволяет сразу
же построить ее аналитическое
уравнение. Однако, если взять две
точки прямой А и В, то кратчайшее
расстояние между ними исчисляется
длиной отрезка [А, В] и любая точка
прямой С, находящаяся между А и В,
будет принадлежать этому отрезку.
Тогда векторы
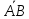 и
и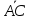 являются коллинеарными и это
справедливо для любых трех точек
прямой. Таким образом, прямая имеет
одну единственную векторную
характеристику, называемую
направляющим вектором.
Дополнив направляющий вектор какой-либо
точкой прямой с помощью линейки,
можно графически построить эту прямую,
причем однозначно. Иными словами,
через заданную точку плоскости в
заданном направлении проходит одна
единственная прямая. Это обстоятельство
убеждает, что таких исходных данных
вполне достаточно для построения
уравнения прямой линии. Итак, пусть
заданы точка прямой
являются коллинеарными и это
справедливо для любых трех точек
прямой. Таким образом, прямая имеет
одну единственную векторную
характеристику, называемую
направляющим вектором.
Дополнив направляющий вектор какой-либо
точкой прямой с помощью линейки,
можно графически построить эту прямую,
причем однозначно. Иными словами,
через заданную точку плоскости в
заданном направлении проходит одна
единственная прямая. Это обстоятельство
убеждает, что таких исходных данных
вполне достаточно для построения
уравнения прямой линии. Итак, пусть
заданы точка прямой
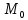 (
(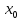 ,
,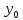 )
и направляющий вектор
)
и направляющий вектор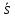 =
= ,
,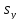 ).
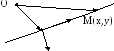
Подведем линейку к точке
).
Подведем линейку к точке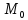 ,
сориентируем ее по указанному
направлению
,
сориентируем ее по указанному
направлению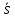 и проведем прямую линию карандашом.
Соответствующие геометрические
построения произведем в системе
координат с центром в точке О. На
изображенном здесь рисунке конкретное
расположение осей координат не
указано, поскольку для последующих
рассуждений это не имеет значения.
Следует отметить, что переход в другую
точку плоскости влечет изменение
координат, поскольку координаты точки
есть величины абсолютные. В
противоположность этому перенос
вектора в другую начальную точку его
координаты не меняет. Таким образом,
для построения уравнения прямой мы
располагаем точкой и вектором,
которые по своей природе являются
принципиально различными объектами.
Кроме того, в рассмотрение необходимо
как-то ввести переменные, присутствующие
в уравнении в обязательном порядке.
При этом желательно одним выстрелом
убить сразу двух зайцев
ввести переменные и заиметь два
объекта, с которыми мы можем производить
какие-либо операции. Такими известными
к настоящему моменту объектами
являются векторы. Если взять еще одну
точку плоскости в дополнении к
заданной, то можно построить второй
вектор в пару к направляющему вектору
прямой. Поскольку мы строим уравнение
прямой, то такую точку логично взять
именно на этой прямой, а чтобы
появились переменные достаточно взять
произвольную точку прямой М(
и проведем прямую линию карандашом.
Соответствующие геометрические
построения произведем в системе
координат с центром в точке О. На
изображенном здесь рисунке конкретное
расположение осей координат не
указано, поскольку для последующих
рассуждений это не имеет значения.
Следует отметить, что переход в другую
точку плоскости влечет изменение
координат, поскольку координаты точки
есть величины абсолютные. В
противоположность этому перенос
вектора в другую начальную точку его
координаты не меняет. Таким образом,
для построения уравнения прямой мы
располагаем точкой и вектором,
которые по своей природе являются
принципиально различными объектами.
Кроме того, в рассмотрение необходимо
как-то ввести переменные, присутствующие
в уравнении в обязательном порядке.
При этом желательно одним выстрелом
убить сразу двух зайцев
ввести переменные и заиметь два
объекта, с которыми мы можем производить
какие-либо операции. Такими известными
к настоящему моменту объектами
являются векторы. Если взять еще одну
точку плоскости в дополнении к
заданной, то можно построить второй
вектор в пару к направляющему вектору
прямой. Поскольку мы строим уравнение
прямой, то такую точку логично взять
именно на этой прямой, а чтобы
появились переменные достаточно взять
произвольную точку прямой М( ).
По правилу сложения радиус-вектор
).
По правилу сложения радиус-вектор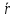 произвольной точки прямой М
произвольной точки прямой М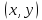 выразится суммой
выразится суммой
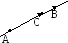
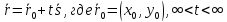 .
.
Данное
уравнение называется векторным
уравнением прямой.
Выбор исходной точки не принципиален,
поскольку для любой другой точки
прямой ее векторное уравнение примет
аналогичный вид. По этой причине
задание прямой ее двумя точками A(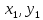 )
и B(
)
и B( )
сводится к первому способу, если
принять в качестве направляющего
вектора
)
сводится к первому способу, если
принять в качестве направляющего
вектора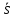 =
= =(
=(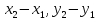 ),
а в качестве исходной точки А или
В
безразлично.
),
а в качестве исходной точки А или
В
безразлично.
Перейдем в векторном уравнении к его координатному представлению
(x,
y)
= ( )
+t
)
+t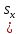 ,
,
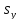 )
= (
)
= (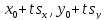 ).
).
Поскольку у равных векторов координаты равны, то распаковывая данное соотношение по каждой координате в отдельности, получим параметрические уравнения прямой
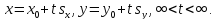
Выражая отсюда
параметр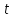 ,
находимканоническое
уравнение
прямой
,
находимканоническое
уравнение
прямой
t
=
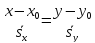 .
.
Заметим, что
равенство в рамке выражает
пропорциональность координат
коллинеарных векторов
 и
и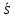 и могло бы быть записано сразу после
определения этих векторов.
и могло бы быть записано сразу после
определения этих векторов.
Приведение пропорции к общему знаменателю дает следующее
уравнение
(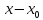 )
)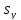 =(
=(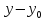 )
)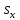 или (
или (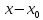 )
)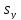 (
(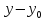 )
)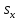 =0.
=0.
Раскрывая скобки, и, группируя постоянные величины, найдем
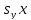
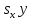 +
(
+
(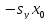 +
+ )=0.
)=0.
После ввода общепринятых обозначений
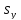 =А,
=А,
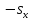 =В,
=В,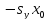 +
+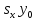 =С
=С
получим так называемое общее уравнение прямой
 .
.
Здесь А и В коэффициенты при переменных, а С свободный член.
При построении
уравнения прямой вместо направляющего
вектора с тем же успехом может быть
задан нормальный
вектор (нормаль)
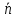 =(
=(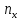 ,
,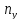 ),
ортогональный направляющему вектору,
т.е.
),
ортогональный направляющему вектору,
т.е.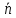 ⊥
⊥
 .
В самом
деле, как это следует из последнего
рисунка, при таких исходных данных
для графического построения прямой
потребуется прямоугольный треугольник.
Если одну его сторону
катет сориентировать по нормали, то
другой катет укажет направление
прямой линии. В этом случае вследствие
.
В самом
деле, как это следует из последнего
рисунка, при таких исходных данных
для графического построения прямой
потребуется прямоугольный треугольник.
Если одну его сторону
катет сориентировать по нормали, то
другой катет укажет направление
прямой линии. В этом случае вследствие
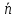 ⊥
⊥
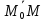 скалярное произведение этих векторов
равно нулю
скалярное произведение этих векторов
равно нулю
 =0
или
=0
или
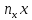 +
+ +
(
+
(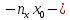
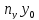 )=0.
)=0.
Обозначив
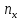 =А,
=А,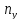 =В,
=В,
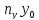 =С,
получим то же самое общее уравнение
прямой. При этом, сопоставляя обозначения
коэффициентов в обоих случаях, находим
связь между значениями координат
нормального и направляющего векторов
=С,
получим то же самое общее уравнение
прямой. При этом, сопоставляя обозначения
коэффициентов в обоих случаях, находим
связь между значениями координат
нормального и направляющего векторов
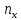 =
=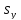 ,
,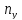 =
=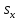 .
.
Вычислив скалярное произведение нормального и направляющего векторов, нетрудно убедиться в их ортогональности
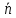
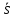 =
=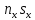 +
+
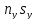 =
=
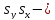
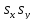 =0.
=0.
Анализ трех последних уравнений прямой линии показывает, что координаты исходной точки и направляющего или нормального вектора формируют коэффициенты уравнений. При этом в общем уравнении коэффициентами при переменных являются координаты нормали, а информация об исходной точке зашифрована в свободном члене. Таким образом, идентификация прямой линии с помощью любой ее точки и направляющего или нормального вектора является конструктивной в смысле построения ее уравнения на основе установленных ранее признаков коллинеарности и ортогональности векторов.
Все рассмотренные уравнения прямой представляют собой способ расчета координат любой ее точки путем смещения из некоторой исходной точки прямой (условно принимаемой в качестве начала отсчета) вдоль направляющего вектора на соответствующую величину, что обеспечивается путем умножения направляющего вектора на параметр t, т.е. его растяжения или сжатия с возможным изменением направления. Поэтому в качестве направляющего подходит любой вектор, указывающий направление прямой с точностью до противоположного. То же самое относится и к нормальному вектору, который может быть сориентирован на любую сторону от прямой линии.
Каждая
прямая задается некоторым линейным
уравнением. Верно и обратное, каждому
линейному уравнению соответствует
некоторая прямая.
В самом деле, развернув произведенные
действия в обратном порядке, нетрудно
проверить, что любое линейное уравнение
своими коэффициентами определяет
нормальный
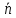 =(А,
В) и направляющий вектор
=(А,
В) и направляющий вектор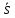 =(В,
А). Теперь, зафиксировав какое-либо
значение одной из переменных, через
уравнение найдем соответствующую
величину другой переменной. Эту пару
чисел (
=(В,
А). Теперь, зафиксировав какое-либо
значение одной из переменных, через
уравнение найдем соответствующую
величину другой переменной. Эту пару
чисел ( ,
,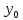 )
будем рассматривать в качестве
координат точки
)
будем рассматривать в качестве
координат точки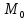 прямой с нормалью
прямой с нормалью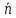 и направляющим вектором
и направляющим вектором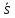 .
.
Таким образом, взяв коэффициенты любого линейного уравне-
ния с двумя переменными, построив направляющий или нормальный вектор по указанному рецепту и дополнив его произвольной точкой, координаты которой удовлетворяют данному уравнению, получим соответствующую прямую на плоскости. В этом и состоит суть геометрической интерпретации линейного уравнения.
Каждое из полученных эквивалентных уравнений прямой линии в конкретной ситуации имеет перед остальными определенные преимущества, и далее будет использоваться сообразно этому обстоятельству.
Пример. Построить все уравнения прямой линии, заданной своим
общим уравнением
l: 2х + 3у + 6 = 0.
Из уравнения
находим
 =(3,
2),
=(3,
2),
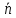 =(2,
3). Определим координаты точек
=(2,
3). Определим координаты точек
пересечения прямой с осями координат, полагая последовательно каждую из переменных равной 0 и вычисляя соответствующее значение другой переменной. При х=0 из уравнения находим y= 2, а при y=0 x= 3. В качестве исходной точки выберем любую из найденных точек
прямой, например,
примем
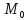 (0,2).
Тогда векторное уравнение прямой
будет иметь следующий вид
(0,2).
Тогда векторное уравнение прямой
будет иметь следующий вид
 (3,
2) =
(3,
2) =
 +2t).
+2t).
Расписывая полученный результат в координатах, сразу же получаем параметрические уравнения
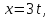
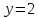 +2t.
+2t.
Исключив параметр t или, что то же самое, вспомнив про пропорциональность соответствующих координат коллинеарных векторов, найдем каноническое уравнение прямой
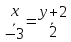 .
.
4.3. Задачи о прямых